Karteesilentokone

Mikä on Cartesian lentokone?

Hän Karteesilentokone Se koostuu parista suorasta viivoista kohtisuorassa toisiinsa nähden ja se leikkaa yhdessä pisteessä. Yksi viivoista on pystysuora ja toinen vaakasuuntainen, ottaen risteyspisteeseen järjestelmän alkuperänä.

Tavoitteena on helposti löytää kaikki tasaiset pisteet arvoparin läpi: koordinaatti. Tätä varten rakennetaan jokaisella rivillä, joissa on kokonaisluku, positiiviset tiedot kirjoitetaan yhteen suuntaan ja negatiivit toisessa, kuten seuraavassa kuvassa esitetään:

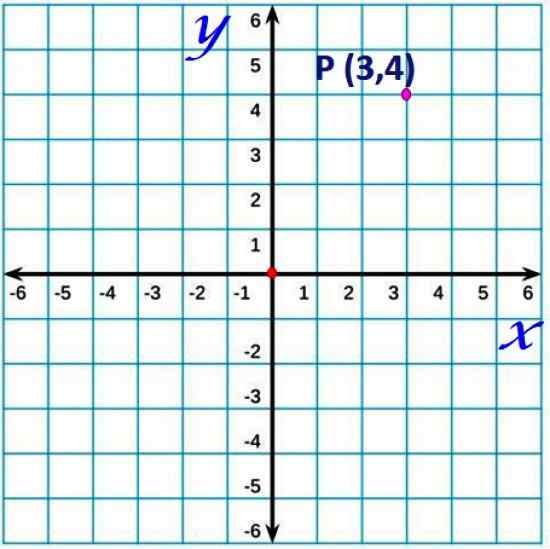
Kuvio 1. Piste Cartesian lentokoneessa. Lähde: f. Zapata.

Kokouksen mukaan vaakasuuntaista akselia kutsutaan yleensä x- ja pystysuuntaiseksi akseliksi ja akseliksi ja.

Minkä tahansa tason pisteellä on koordinaatit, jotka on määritelty järjestyksessä (X, y). Esimerkiksi koordinaatin (3,4) kohta P, joka sijaitsee 3 yksikköä alkuperäisen oikealla puolella ja 4 yksikköä ylöspäin, ylemmässä kuvassa. Se on samanlainen kuin kartta, joka osoittaa tietyn sijainnin leveys- ja pituuden ja pituuden.

Koska kaksi koordinaattia on välttämätöntä, sanotaan, että taso on kaksiulotteinen, mutta konsepti laajennetaan helposti kolmeen ulottuvuuteen lisäämällä koordinaattiakselia, joka yleensä merkitään Z -akseliksi. Tässä tapauksessa koordinaatit muotoutuvat (X ja z).

Cartesian lentokone saa nimensä ranskalaiselta tiedemieheltä René Descartesilta (1596-1650), joka virallisti sen työssään Menetelmäpuhe 1637: stä, vaikka Pergan Apollonius-teoksissa (262-190 AC) on, matemaatikko, joka löysi kartiomaiset käyrät: kehys, ellipsi, vertaus ja hyperbola.

Voi palvella sinua: Kuutiot: Kaavat, yhtälöt, esimerkit, harjoitukset

Cartesian -lentokoneen ominaisuudet

- Kuten hän X -akseli Kuin Akseli y Ne ulottuvat äärettömästi molemmissa päissä ja leikkaavat yhteen kohtisuorasti (90 asteen kulmassa). Tätä ominaisuutta kutsutaan ortogonaalisuudeksi.

- Piste, jossa molemmat akselit leikkaus, tunnetaan nimellä alkuperän tai nollapisteen.

- Koordinaattijärjestelmä jakaa koneen neljään alueelle, nimeltään kvadrantsiksi.

- Koordinaattiasen sijainnit kuvataan tilatuina pareina.

- Jokainen Cartesian -tason piste liittyy ainutlaatuiseen X -koordinaattiin ja koordinaattiin ja ainutlaatuiseen.

Cartesian lentokoneen elementit

Cartesian lentokoneen elementit ovat seuraavat:

-Se numeeriset linjat jompikumpi koordinaattiakselit x ja y, Jos se on kone. Akseli ja vastaanottaa ordinaattien akselin nimi, kun taas akseli x Se on abskissan akseli. Kun kyse on avaruudesta, akseli lisätään z -z, pystyy edustamaan sekä korkeutta että syvyyttä.

-Hän alkuperä, mikä on akselien leikkauspiste.

-Se kvadrantit, jotka ovat alueet, jotka koordinaattiakselit määrittävät tasossa ja lasketaan vastakkaiseen suuntaan kuin kellon kädet alkaen ensimmäisestä kvadrantista. Ne määritellään seuraavasti:

• Ensimmäinen kvadrantti: akselit x ja ja positiivinen.
• Toinen kvadrantti: vastaa negatiivista X -akselia ja ja positiivista akselia.
• Kolmas kvadrantti: Siinä on molemmat negatiiviset akselit.
• Neljäs kvadrantti: positiivisella X -akselilla ja negatiivisella akselilla.

Yleensä kvadrantit on merkitty roomalaisina lukuina, kuten tämä:

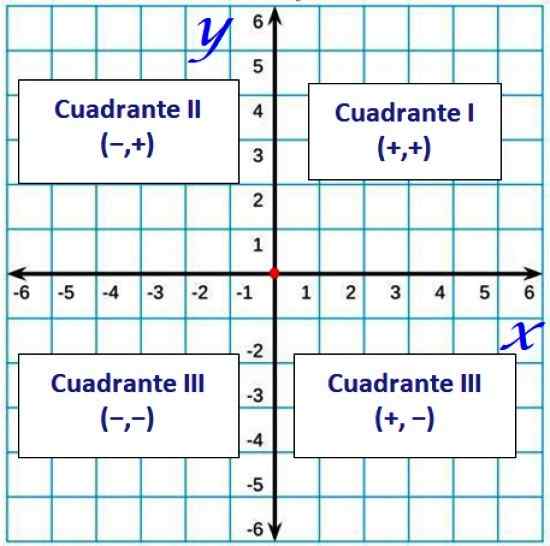Kuva 2. Cuadrants Cartesian lentokoneessa. Lähde: f. Zapata.

Tilattu parit ja kahden pisteen välinen etäisyys

Tilatut parit ovat kunkin pisteen koordinaatit, joissa X -koordinaatti sijoitetaan aina ensin, kuten kuvan 1 esimerkissä. Kohdan P koordinaatit (3,4) osoittavat sen x = 3 ja y = 4.

Tässä muussa kuvassa Piste P kuuluu IV -kvadranttiin ja sillä on koordinaatit (2; −1.5). Huomaa, että projisoimalla viivoja koordinaattiakselista pisteeseen P muodostaa suorakulmion. Tästä syystä Cartesian -koordinaatit kutsutaan myös suorakulmaiset koordinaatit.

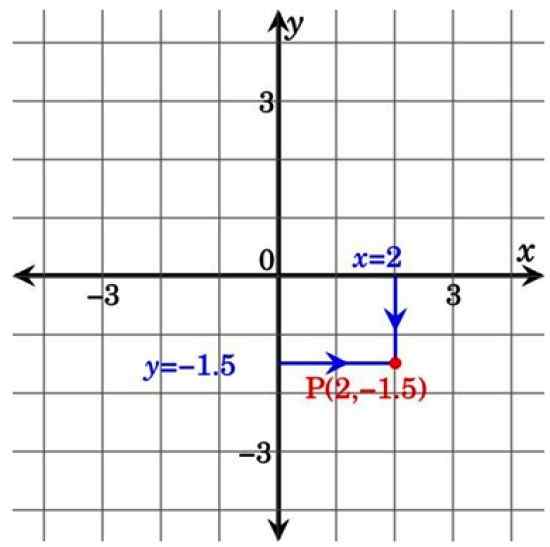Kuva 3. Piste Cartesian lentokoneessa. Lähde: Wikimedia Commons.

Cartesian lentokonesovellukset

Cartesian lentokoneessa on monia sovelluksia monilla aloilla. Aluksi Descartes esitteli sen tason käyrien graafiseen käyriin, minkä vuoksi sitä pidetään analyyttisen geometrian isänä.

Voi palvella sinua: Cruz -tuote

Sen käyttö ulottuu kuitenkin kaikenlaisten suhteiden ja toimintojen, kuten:

-Seuraa kehon suuntausta, jolla on yleensä parabolinen, pyöreä tai kaareva liike.

-Määritä graafisesti tapa, jolla kaksi muuttujaa liittyy funktion kautta.

-Etsi pisteet tasaiselle maalle mittausten helpottamiseksi.

Viitteet

1. Matematiikka on hauskaa. Cartesian koordinaatit. Toipunut: MathSisfun.com/data/Cartesian-koordinaatit.
2. Cartesian lentokone. Haettu osoitteesta: DL.Ucw.Edu.