Mekaaninen voima mikä on, sovellukset, esimerkit

Se Mekaaninen voima Se on rytmi, jolle työ tehdään, joka ilmaistaan ​​matemaattisella tavalla aikayksikköä kohti tehdyn työn määrään. Ja koska työ tehdään absorboituneen energian kustannuksella, sitä voidaan nostaa myös energiana aikayksikköä kohti.

Kutsumus P valtaan, W - työskennellä, JA energialle ja t Samanaikaisesti kaikki yllä olevat voidaan tiivistää matemaattisten ilmaisujen helposti käsittelemisessä:

Kuvio 1. Gossamer Albatross, "Lentävä polkupyörä", ylitti La Manchan kanavan 1970 -luvun lopulla käyttämällä vain ihmisvoimaa. Lähde: Wikimedia Commons. Gossamer albatross. Guroadrunner English Wikipediassa [julkinen alue]

O No:

Kansainvälisen järjestelmän (SI) voimayksiköt, jotka ovat yleisesti hyväksyttyjen yksiköiden järjestelmä, ovat joule/toinen tai watt, joka lyhennetään W. Se nimettiin siten skotlantilaisen insinöörin James Wattin (1736-1819) kunniaksi, joka tunnetaan perustavan höyrykoneen lauhduttimen kanssa, keksintö, joka aloitti teollisuuden vallankumouksen.

Muita teollisuudenaloilla käytettyjä sähköyksiköitä ovat HP (Hevosvoimaa tai voimahevonen) ja CV (höyryhevonen). Näiden yksiköiden alkuperä on myös juurtunut James Wattiin ja teollisuusvallankumoukseen, kun mittausmalli oli rytmi, jolla hevonen työhön.

Sekä HP että CV vastaavat noin ¾ kilo-w: tä edelleen paljon, etenkin konetekniikassa, esimerkiksi moottorien nimeämisessä.

Watt-kertoimia, kuten edellä mainittua kilo-W = 1000 W, käytetään myös usein sähköllä. Se johtuu siitä, että Joule on suhteellisen pieni energiayksikkö. Brittiläinen järjestelmä käyttää Vaaka-pie/toinen.

[TOC]

Mikä on teollisuus- ja energiasovellukset

Voimakonseptia voidaan soveltaa kaikentyyppisiin energiaan, onko mekaaninen, sähköinen, kemiallinen, tuuli, sononiikka tai minkä tahansa tyyppinen. Aika on erittäin tärkeä alalla, koska prosessit on suoritettava mahdollisimman nopeasti.

Jokainen moottori tekee tarvittavan työn riittävästi aikaa, mutta tärkeä asia on tehdä se lyhyimmässä mahdollisessa ajassa, lisätäkseen tehokkuutta.

Hyvin yksinkertainen sovellus kuvataan välittömästi työn ja voiman välisen eron selventämiseksi.

Oletetaan, että köydellä keskeytetään raskas esine. Tätä varten vaaditaan tarvittava työ. Sanotaan.

Voi palvella sinua: Cross Wave

Tässä tapauksessa energiansiirtonopeus on 90 J/10 s tai 9 j/s. Sitten voimme vakuuttaa, että tällä agentilla, henkilöllä tai moottorilla on 9 W: n lähtöteho.

Jos toinen ulkoinen aine pystyy saavuttamaan saman siirtymän, joko vähemmän ajassa tai siirtämällä vähemmän energiaa, se kykenee kehittämään suurempaa voimaa.

Toinen esimerkki: Oletetaan, että energiansiirto on 90 J, joka onnistuu siirtämään järjestelmää 4 sekunnin ajan. Lähtöteho on 22.5 W.

Koneen suorituskyky

Power liittyy läheisesti suorituskykyyn. Koneelle toimitettua energiaa ei koskaan muuteta täysin hyödylliseksi työksi. Tärkeä osa häviää yleensä lämmössä, mikä riippuu monista tekijöistä, esimerkiksi koneen suunnittelusta.

Siksi on tärkeää tietää koneiden suorituskyky, joka on määritelty toimitetun työn ja toimitetun energian väliseksi suhteeksi:

η = toimitetun koneen/energian toimittama työ

Missä kreikkalaiset lyrics η Tarkoittaa suorituskykyä, lisämäärää, joka on aina alle 1. Jos kerrot myös 100: lla, sinulla on suorituskyky prosentteina.

Esimerkit

- Ihmisillä ja eläimillä kehittyy voimaa liikkumisen aikana. Esimerkiksi portaiden kiipeilyssä on tarpeen tehdä työtä painovoimaa vastaan. Kahden tikkaiden nousevan ihmisen vertaaminen, jotka nousevat ensin kaikkiin askeleisiin, on kehittänyt enemmän voimaa kuin toiset, mutta molemmat tekivät saman työn.

- Laitteet ja koneet määritetään niiden lähtöteho. Asianmukaisen hehkulampun huoneen valaistuen valaistukseen on 100 W: n voima. Tämä tarkoittaa, että lamppu muuttaa sähkön valoksi ja lämmöksi (eniten) nopeudella 100 J/s.

- Ruohon karsimisen moottori voi kuluttaa noin 250 W ja auton moottori on 70 kW: n järjestyksessä.

- Kotitekoiset vesipumpputarvikkeet yleensä 0.5 hv.

- Aurinko tuottaa 3.6 x 10 ²⁶ W -voima.

Ja nopeus

Pikavoima saadaan ottamalla ääretön aika: P = DW/DT. Pienen äärettömän siirtymän aiheuttama työvoima d -dx On F (molemmat ovat vektoreita), siksi dw = F ● d -dx. Kaiken voiman ilmaisun korvaaminen pysyy:

Voi palvella sinua: Keskipakovoima: Kaavat, miten se lasketaan, esimerkkejä, harjoituksia

Siksi teho voidaan ilmaista myös skalaarituotteena voiman ja nopeuden välillä.

Ihmisvoima

Ihmiset kykenevät tuottamaan noin 1500 W tai 2 hevosvoimaa ainakin lyhyen aikaa, kuten painopainot.

Päivittäinen tehon (8 tuntia) on keskimäärin 0.1 hv henkilöä kohti. Suuri osa siitä tarkoittaa lämpöä, enemmän tai vähemmän sama määrä, jonka syntyy hehkulamppu 75 W.

Harjoitteluurheilija voi tuottaa keskimäärin 0.5 hv, joka vastaa noin 350 J/s, muuttamalla kemiallinen energia (glukoosi ja rasva) mekaaniseksi energiaksi.

Kuva 2. Urheilija kehittää keskimääräisen voiman 2 hv. Lähde: Pixabay.

Ihmisen voiman suhteen se on yleensä suositeltavaa. Tarvittava vastaavuus on:

1 kilocaloria = 1 ravitsemuskalori = 4186 J

Teho 0.5 hv kuulostaa hyvin pieneltä määralta, ja se on tarkoitettu monille sovelluksille.

Kuitenkin vuonna 1979 ihmisen työntämä polkupyörä voi kuitenkin lentää. Paul Maccready suunnitteli Gossamer albatross, joka ylitti La Mancha -kanavan, joka tuotti 190 W keskimääräistä lähtöä (kuva 1).

Sähköenergian jakautuminen

Tärkeä sovellus on sähkön jakelu käyttäjien keskuudessa. Yritykset, jotka toimittavat sähkölaskun kulutettua energiaa, eivät sen kuluttamisaste. Siksi ne, jotka lukevat laskunsa huolellisesti.

Kuitenkin, kun Wattin nimi sisältyy tähän yksikköön, viittaa energiaan eikä voimaan.

Kilowatt-horaa käytetään osoittamaan sähkön kulutusta, koska Joule, kuten aiemmin mainittiin, on melko pieni yksikkö: 1 watt-hora tai W-H Se on työ, joka tehdään tunnissa 1 watin voiman läpi.

Siksi 1 kW-H Työt tehdään tunnissa työskentelemällä 1 kW: n tai 1000 W: n kanssa. Laitetaan numerot näiden määrien välittämiseksi Joulesille:

1 W-H = 1 W x 3600 S = 3600 J

1 kW-H = 1000 W x 3600 s = 3.6 x 10 ⁶ J -

Arvioidaan, että kodissa noin 200 kW-hora voidaan kuluttaa kuukaudessa.

Se voi palvella sinua: Absoluuttinen paine: kaava, miten se lasketaan, esimerkkejä, harjoituksia

Harjoitukset

Harjoitus 1

Viljelijä käyttää traktoria vetääkseen heinän PacA: ta M = 150 kg 15 °: n kaltevalle tasolle ja viedä se navettaan vakiona 5.0 km / h. Heinän fardon ja rampin välinen kineettisen kitkakerroin on 0.Neljä viisi. Etsi traktorin lähtöteho.

Ratkaisu

Tätä ongelmaa varten on tarpeen piirtää ilmainen kehon kaavio heinän fardolle, joka nousee kaltevalle tasolle. Olla F Traktoria soveltavan voima kiivetä bundoon, α = 15º on kallistuskulma.

Lisäksi mukana on kineettinen kitkavoima F_kosketus jotka vastustavat liikettä sekä normaalia N ja paino W - (Älä sekoita painon W työn painoa).

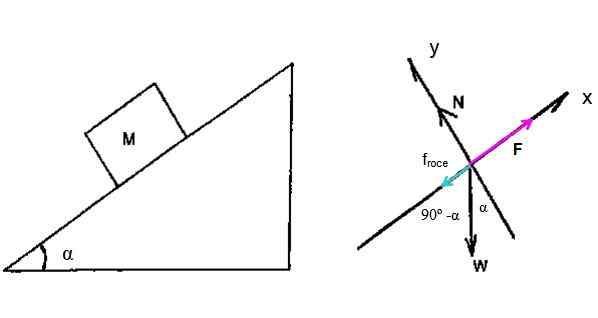Kuva 3. Heo fardo eristetty kehon kaavio. Lähde: f. Zapata.

Newtonin toinen laki tarjoaa seuraavat yhtälöt:

∑ fx = f -w_x -F_kosketus = 0 (Koska Bundo nousee vakiona nopeudella)

∑fy = n - w_ja = 0 (X -akselia pitkin ei ole liikettä)

Kineettinen kitka on laskettu:

F_kosketus = Kineettinen kitkakerroin x normaalin suuruus

F_kosketus = 0.Neljä viisi . WY = 0.45 x 150 kg x9.8 m/s2 x cos 15º = 639 n

F = w_x + F_kosketus = M.g. synti α = 150 kg. 9.8 m/s² . sin 15 º + 639 n =  1019.42 n

Nopeudella ja lujuudella on siksi sama suunta ja merkitys:

P = F ● v = F. v

Sitä tarvitaan nopeusyksiköiden muuttamiseksi:

V = 5.0 km/ h = 1.39 m/ s

Korvataan arvot, saat vihdoin:

P = 1019.42 n x 1.39 m/ s = 1417 W = 1.4 kW

Harjoitus 2

Kuvassa näkyvä moottori lähettää 2 kg -lohkon leposta alkaen, kiihtyvyyden ollessa 2 m/s² Ja 2 sekunnissa.

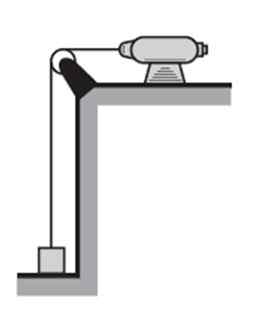Kuva 4. Moottori nostaa esineen tietylle korkeudelle, jota varten on tarpeen tehdä työtä ja kehittää virtaa. Lähde: f. Zapata.

Laskea:

a) Korkeus, jonka lohko saavutti tuolloin.

b) moottorin kehitettävä voima sen saavuttamiseksi.

Ratkaisu

a) Se on tasaisesti vaihteleva välirektilinarinen liike, joten käytetään vastaavia yhtälöitä, alkuperäisen nopeuden 0 ollessa 0. Saavutettu korkeus annetaan:

y = ½² = ½ . 2 m/s² . (2 s)² = 4 m.

b) Löydä moottorin kehittämä teho yhtälöä voidaan käyttää:

P = δW/Δt

Ja koska lohkoon kohdistuva voima on köyden jännityksen läpi, joka on vakiona suuruudessa:

P = (ma).ja/ΔT = 2 kg x 2 m/s² x 4 m / 2 s = 8 W

Viitteet

1. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Nide 2. Dynaaminen. Toimittanut Douglas Figueroa (USB).
2. Ritari, r.  2017. Tutkijoiden fysiikka ja tekniikka: strategialähestymistapa.  Pearson.
3. Fysiikka librettexts. Voima. Toipunut: Phys.Librettexts.org
4. Fysiikan hypertekstin kirja. Voima. Toipunut: fysiikka.Tiedot.
5. Työ, energia ja voima. Palautettu: NCERT.Nivel.sisään