Sähköpotentiaali kaava ja yhtälöt, laskenta, esimerkit, harjoitukset

Hän sähköinen potentiaali Se on määritelty missä tahansa vaiheessa, jossa on sähkökenttä, kuten mainitun kentän potentiaalinen energia kuormitusyksikköä kohti. Erityisten tai jatkuvien kuormitusten erityiset kuormat ja jakaumat tuottavat sähkökenttää, ja siksi niihin liittyy potentiaalinen.

Kansainvälisessä yksikköjärjestelmässä (SI) sähköpotentiaali mitataan volteina (V) ja se merkitään V: ksi. Matemaattisesti ilmaisee seuraavasti:

V = u/q_jompikumpi

Kuvio 1. Akkuun kytkettyjä apukaapeleita. Lähde: Pixabay.

Missä u on kuormitukseen tai jakeluun liittyvä potentiaalienergia ja q_jompikumpi Se on positiivinen koekuorma. Koska u on skalaari, myös potentiaali on.

Määritelmästä 1 voltti on yksinkertaisesti 1 joule /coulomb.

Oletetaan, että täsmällinen taakka. Voimme tarkistaa kentän luonteen, jonka tämä kuorma tuottaa positiivisen ja pienen koekuorman, nimeltään Q_jompikumpi, Käytetty koettimena.

Työ tarvitaan tämän pienen kuorman siirtämiseksi pisteestä -lla Kohteeseen asti b -, on negatiivinen eron suhteen Mahdollinen energia ΔU näiden pisteiden välillä:

W -_{a → b} = -AU = - (U_{b -} - TAI_-lla-A      

Jakamalla kaikki q: n välillä_jompikumpi-

W -_{a → b} /Q_jompikumpi= - ΔU / Q_jompikumpi = - (u_{b -} - TAI_-lla) /Q_jompikumpi = - (v_{b -} - V_-lla) = -AV

Täällä v_{b -} Se on potentiaali kohdissa B ja V_-lla on kohta a. Potentiaaliero v_-lla - V_{b -}  on potentiaali B: n suhteen ja sitä kutsutaan V_Ab. Tilausten järjestys on tärkeä, jos sitä muutettaisiin, niin potentiaali B.

[TOC]

Sähköpotentiaalierot

Edellä mainitusta seuraa, että:

-ΔV = W_{a → b} /Q_jompikumpi

Siksi:

Δv = -W_{a → b} /Q_jompikumpi

Nyt työ lasketaan skalaarituotteen integraaliksi sähkövoiman välillä F Q: n ja Q: n välillä_jompikumpi ja siirtymävektori Dℓ Pisteiden A ja B välillä. Koska sähkökenttä on voima kuormitusyksikköä kohti:

JA = F/Q_jompikumpi

Testikuorman kuljettaminen A: sta B: hen on:

Tämä yhtälö tarjoaa tavan laskea potentiaaliero suoraan, jos sitä tuottava sähkö- tai jakelukenttä on aiemmin tunnettu.

Ja myös varoitetaan, että potentiaalioero on skalaarinen määrä, toisin kuin sähkökenttä, joka on vektori.

Voi palvella sinua: Magnetismi: materiaalien magneettiset ominaisuudet, käyttötarkoitukset

Merkit ja arvot potentiaalieron kannalta

Edellisestä määritelmästä havaitsemme, että jos JA ja Dℓ Ne ovat kohtisuorassa, potentiaaliero ΔV on nolla. Tämä ei tarkoita, että potentiaali tällaisissa kohdissa on nolla, mutta yksinkertaisesti v_-lla = V_{b -}, toisin sanoen potentiaali on vakio.

Linjoja ja pintoja, joissa tämä tapahtuu, kutsutaan Joukkueet. Esimerkiksi täsmällisen kuormituksen kentän laitteet ovat samankeskisiä kehitystä kuormaan. Ja TeamCotential -pinnat ovat samankeskisiä palloja.

Jos potentiaalia tuottaa positiivinen kuorma, jonka sähkökenttä koostuu lähtevästä radiolinjasta. Kuten koekuorma q_jompikumpi Se on positiivinen, se tuntuu vähemmän sähköstaattiselta torjumisesta, mitä kauempana se on Q: sta.

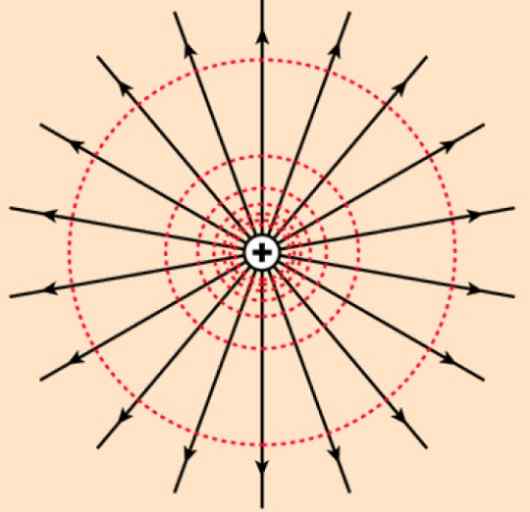Kuva 2. Positiivisen täsmällisen kuormituksen ja sen laitteiden (punaiset) linjat: Wikimedia Commons -sovelluksen tuottama sähkökenttä. Hyperfysiikka/CC BY-SA (https: // creativecommons.Org/lisenssit/by-SA/4.0).

Päinvastoin, jos kuorma Q - Se on negatiivinen, koekuorma Q_jompikumpi (positiivinen) on vähemmän potentiaalia lähestyessään Q -.

Kuinka laskea sähköpotentiaali?

Edellä annettu integraali tarjoaa potentiaalieron ja siten potentiaalin tietyssä pisteessä b -, Jos referenssipotentiaali tunnetaan toisessa vaiheessa -lla.

Esimerkiksi on olemassa täsmällinen kuorma Q -, jonka sähkökenttävektori etäisyydellä sijaitsevassa pisteessä r - kuormituksesta on:

JA = kq/r² r -

Missä k on sähköstaattinen vakio, jonka arvo kansainvälisen järjestelmän yksiköissä on:

K = 9 x 10 ⁹ Nm² /C².

Ja vektori r - Se on yksikkövektori linjaa pitkin Q - Pisteellä P.

Se korvataan määritelmässä ΔV-

Pisteen valitseminen b - olla etäisyydellä r - kuormituksesta ja siitä, milloin → ∞ potentiaali on 0, niin V_-lla = 0 ja edellinen yhtälö on seuraavasti:

V = kq/r

Valitse V_-lla = 0 Kun → ∞, se on järkevä.

Sähköinen potentiaali erillisille kuormitusjakaumille

Kun alueella on jaettuja erityisiä kuormituksia, niiden tuottama sähköpotentiaali on laskettu missä tahansa tilan P: ssä, lisäämällä kunkin tuottamat yksilölliset potentiaalit. Niin:

Voi palvella sinua: elliptinen liike

V = V₁ + V₂ + V₃ +… Vn = ∑ V_Yllyttää

Summa pidennetään välillä i = - n ja kunkin kuorman potentiaali lasketaan edellisessä osassa annettulla yhtälöllä.

Sähköpotentiaali jatkuvassa kuormitusjakaumissa

Alkaen täsmällisen kuorman potentiaalista löydät potentiaalin, joka tuottaa ladatun objektin mitattavissa olevalla koolla, missä tahansa vaiheessa P.

Tätä varten vartalo on jaettu moniin pieniin äärettömiin kuormituksiin dq. Kukin myötävaikuttaa kokonaispotentiaaliin a DV ääretön.

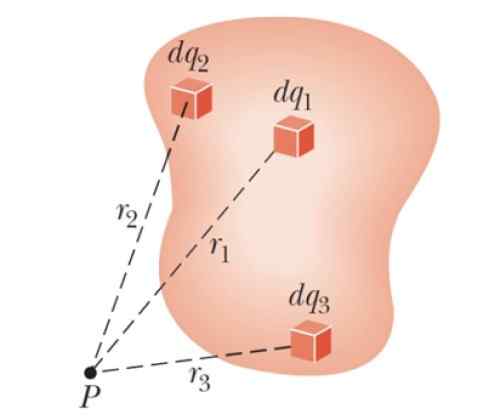Kuva 3. Kaavio jatkuvan jakautumisen sähköpotentiaalin löytämiseksi kohdassa P. Lähde: Serway, R. Fysiikka tieteen ja tekniikan fysiikka.

Sitten kaikki nämä panokset lisätään integraalilla ja siten kokonaispotentiaali saadaan:

Tämä menetelmä mahdollistaa potentiaalieron laskemisen tuntematta aiemmin sähkökenttää, mutta sitä käytetään vain äärellisiin kuormitusjakaumiin, kuten erittäin ohuet palkit ja rajallinen pituus, renkaat, levyt ja sylinterit, esimerkiksi äärellinen pituus, esimerkiksi rajallinen pituus, esimerkiksi.

Esimerkkejä sähköpotentiaalista

Eri laitteilla on sähköpotentiaalia, mikä on mahdollista. Sähköpotentiaalit ovat myös luonteeltaan, kun ukkosta on.

Paristot ja paristot

Paristoissa ja paristoissa sähkö säilytetään sisällä olevien kemiallisten reaktioiden kautta. Ne tapahtuvat, kun piiri sulkeutuu, jolloin jatkuvaa virtaa voi virtaa ja lamppu kytketään päälle tai auton aloitusmoottori toimii.

Jännitteitä on useita: 1.5 V, 3 V, 9 V ja 12 V ovat tavallisimpia.

Pistorasia

Rakennetulle seinälle laukaukselle. Paikasta riippuen jännite voi olla 120 V tai 240 V.

Kuva 4. Seinän ottamisessa on potentiaalinen ero. Lähde: Pixabay.

Lastattujen pilvien ja maan välinen jännite

Se esiintyy myrskyjen aikana, koska ilmakehän läpi on sähkövarausliike. Se voi olla luokkaa 10⁸ V.

Kuva 5. Sähkömyrsky. Lähde: Wikimedia Commons. Sebastien D'Ec Arc, Koba-chan/cc by-sa (https: // creativecommons.Org/lisenssit/by-SA/2.5)

Van der Graff -generaattori

Kuljetinkuminauhan ansiosta hankaaminen tuotetaan hankauksella, joka kertyy johtavan palloon eristyssylinteriin. Tämä tuottaa potentiaalieron, joka voi olla useita miljoonia voltteja.

Voi palvella sinua: Konvektio Kuva 6. Van der Graff -generaattori Boston Sciences -museon sähköteatterissa. Lähde: Wikimedia. Bostonin tiedemuseo/CC BY-S (https: // creativecommons.Org/lisenssit/by-SA/3.0) Commons.

Elektrokardiogrammi ja elektroenkefalogrammi

Sydämessä on erikoistuneita soluja, jotka polarisoivat ja depolarisoivat alkuperäiset potentiaaliset erot. Ne voidaan mitata ajasta riippuen elektrokardiogrammilla.

Tämä yksinkertainen koe suoritetaan asettamalla elektrodit henkilön rintaan, joka pystyy mittaamaan pienet signaalit.

Koska ne ovat erittäin pieniä jännitteitä, sinun on vahvistettava niitä kätevästi ja sitten tallennettava ne paperiteipille tai katsottava ne tietokoneen läpi. Lääkäri analysoi pulssit etsiessään poikkeavuuksia ja havaitsee siten sydänongelmat.

Kuva 7. Painettu elektrokardiogrammi. Lähde: PxFuel.

Aivojen sähköinen aktiivisuus voidaan myös tallentaa samanlaisella menettelyllä, nimeltään elektroenkefalogrammi.

Liikuntaa

Kuorma Q - = - 50.0 NC sijaitsee 0.30 m pistettä -Lla ja 0.50 m piste B, kuten seuraavassa kuvassa esitetään. Vastaa seuraaviin kysymyksiin:

a) mikä on tämän kuorman tuottaman potentiaali?

b) ja mikä on potentiaali b: ssä?

c) Jos kuorma, joka siirtyy A: sta B: hen B, mikä on potentiaaliero, jonka kautta se tekee?

d) Edellisen vasteen mukaan sen potentiaalinen lisääntyminen tai väheneminen?

e) kyllä ​​q = - 1.0 NC, mikä on sähköstaattisen potentiaalienergian muutos siirtyessäsi A: sta B: hen?

f) kuinka paljon työtä Q: n tuottama sähkökenttä on, kun testikuorma siirtyy A: sta B: hen?

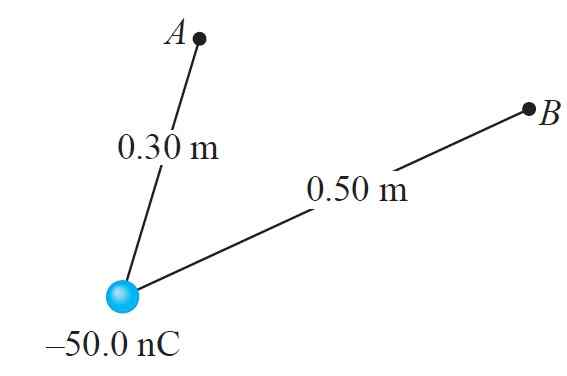Kuva 8. Harjoitusjärjestelmä ratkaistu. Lähde: Giambattista, a. Fysiikka.

Liittää jhk

Q on täsmällinen kuorma, joten sen sähköpotentiaali A: ssa lasketaan:

V_-Lla = kq/r_-Lla = 9 x 10⁹ X (-50 x 10^-9) / 0.3 V = -1500 V

Ratkaisu b

samalla lailla

V_{B -} = kq/r_{B -} = 9 x 10⁹ X (-50 x 10^-9) / 0.5 V = -900 V

Liuos C

Δv = v_{b -} - V_-lla = -900 -( -1500) V = + 600 V

Liuos D

Jos positiivinen kuorma, sen potentiaali kasvaa, mutta jos se on negatiivinen, sen potentiaali vähenee.

Ratkaisu E

ΔV = ΔU/Q_jompikumpi → ΔU = Q_jompikumpi Δv = -1.0 x 10^-9 x 600 J = -6.0 x 10^-7 J -.

Negatiivinen kirjain ΔU osoittaa, että potentiaalinen energia B: ssä on pienempi kuin a.

Liuos f

Koska W = -A, kenttä toimii +6.0 x 10^-7 J - työn.

Viitteet

1. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Nide 5. Sähköstaatiikka. Toimittanut Douglas Figueroa (USB).
2. Giambattista, a. 2010. Fysiikka. Toinen. Ed. McGraw Hill.
3. Resnick, r. (1999). Fyysinen. Osa. 2. 3. ed. espanjaksi. Mannertoimitusyhtiö S.-Lla. C: n.V.
4. Tipler, P. (2006) Tieteen ja tekniikan fysiikka. 5. ed. Nide 2. Toimitus palautti.
5. Serway, R. Fysiikka tieteen ja tekniikan fysiikka. Nide 2. Seitsemäs. Ed. Cengage -oppiminen.