Antidervatiiviset kaavat ja yhtälöt, esimerkit, harjoitukset

Eräs ykkös- F (x) funktio F(x) kutsutaan myös primitiiviseksi tai yksinkertaisesti mainitun funktion määrittelemätön integraali, jos tietyllä aikavälillä Yllyttää, Onko totta että F '(x) = f (x)

Otetaan esimerkiksi seuraava toiminto:

f (x) = 4x³

Tämän funktion antipää on f (x) = x⁴, koska johdetaan f (x): n johdannaisääntöjen avulla:

Se saadaan tarkalleen f (x) = 4x³.

Tämä on kuitenkin vain yksi monista f (x): n monista antiderivatiivista, koska tämä toinen funktio: g (x) = x⁴ + 2 Se on myös, koska johdettamalla g (x) x: n suhteen, se on sama, joka saadaan takaisin f (x).

Tarkistetaan se:

Muista, että vakiosta johdettu on 0. Siksi termiin x⁴ Voit lisätä vakiona ja sen johdannainen on edelleen 4x³.

Johtopäätöksenä on, että yleisen lomakkeen f (x) = x funktio⁴ + C, missä C on todellinen vakio, toimii F (x): n antiderivisinä.

Aikaisempi havainnollistava esimerkki voidaan ilmaista seuraavasti:

df (x) = 4x³ Dx

Määrittelemätön antidervatiivinen tai integraali ilmaistaan ​​symbolilla ∫, siksi:

F (x) = ∫4x³ dx = x⁴ + C

Missä funktio f (x) = 4x³  Sitä kutsutaan integroiva, ja c on Integraatiovakio.

[TOC]

Esimerkkejä antidervanitioista

Kuvio 1. Anti -Hotley ei ole muuta kuin määrittelemätön integraali. Lähde: Pixabay.

Funktion antipäätoimituksen löytäminen on yksinkertaista joissain tapauksissa, joissa johdannaiset ovat hyvin tunnettuja. Esimerkiksi, ole funktio f (x) = Sen X, sen oppimattomana on toinen funktio F (x) siten, että johdettuna se saadaan f (x).

Tämä toiminto voi olla:

F (x) = - cos x

Tarkistetaan, että se on totta:

F '(x) = (- cos x)' =- (-sen x) = sin x

Siksi voimme kirjoittaa:

∫sen x dx = -cos x + c

Johdannaisten tuntemisen lisäksi on olemassa perus- ja yksinkertaisia ​​integraatiosääntöjä, jotka löytyvät määrittelemättömästä antiDervativeista tai integroinnista.

Voi palvella sinua: peräkkäiset johdannaiset

Ole sitten todellinen vakio,:

1.- ∫kdx = k ∫dx = kx + c

2.- ∫kf (x) dx = k ∫f (x) dx

Jos H (x) -funktio voidaan ilmaista kahden funktion summana tai vähentämisenä, sen määrittelemätön integraali on:

3.- ∫h (x) dx = ∫ [f (x) ± g (x)] dx = ∫f (x) dx ± ∫g (x) dx

Tämä on lineaarisuuden ominaisuus.

Se Vallansääntö Integraaleille se voidaan perustaa tällä tavalla:

Tällä säännöllä on ilmeinen rajoitus: nimittäjän jälkeen N +1 Sitä ei voida tehdä 0, siksi n ≠ -1.

N = -1: n tapauksessa käytetään seuraavaa sääntöä:

5.- ∫x ^-1 Dx = ln x +c

On helppo osoittaa, että johdannainen ln x se on juuri x ^-1.

Differentiaaliyhtälöt

Differentiaaliyhtälö on sellainen, jossa tuntematon on johdannainen.

Nyt edellisestä analyysistä on helppo ymmärtää, että johdannaisen käänteinen toimenpide on määrittelemätön antiDervative tai Integraal.

Olkoon f (x) = y '(x), ts. Voimme käyttää seuraavaa merkintää osoittaaksesi tämän johdannaisen:

Se seuraa heti:

dy = f (x) dx

Differentiaaliyhtälön tuntematon on funktio y (x), joka, jonka johdannainen on f (x). Sen puhdistamiseksi edellinen lauseke on integroitu molemmille puolille, mikä vastaa antidervatiivisen soveltamista:

∫Dy = ∫f (x) dx

Vasen integraali ratkaistaan ​​integraatiosääntöllä 1, K = 1: n kanssa ja siten haluttu -Awaite puhdistetaan:

ja (x) = ∫f (x) dx = f (x) + c

Ja koska C on todellinen vakio, tietää, mikä on asianmukaista kussakin tapauksessa, lausunnossa on oltava riittävä lisätietoja C: n arvon laskemiseksi. Tätä kutsutaan Alkuolosuhde.

Näemme esimerkkejä kaiken tämän soveltamisesta seuraavassa osassa.

Voi palvella sinua: Täsmällinen arvio

Antideriviset harjoitukset

- Harjoitus 1

Käytä integrointisääntöjä seuraavien määrittelemättömien antilivatiivisten tai toimintojen integraalien hankkimiseksi, yksinkertaistaen tuloksia niin paljon kuin mahdollista. On kätevää tarkistaa tulos johdannaisella.

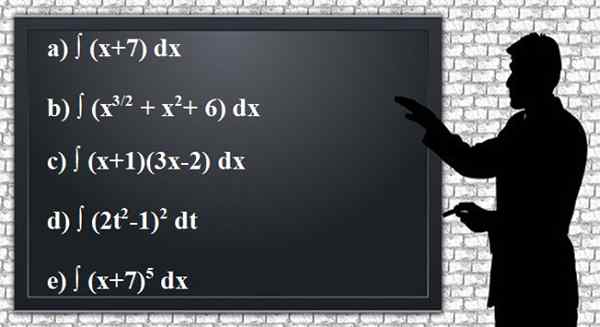Kuva 2. Määritetyt anteesi- tai integraaliharjoitukset. Lähde: Pixabay.

Liittää jhk

Käytämme ensin sääntöä 3, koska integrointi on kahden termin summa:

∫ (x +7) dx = ∫ xdx +∫7dx

Ensimmäisen integraalin suhteen sovelletaan valtuuksien sääntöä:

∫ XDX = (x² /2)+c₁

Toisessa integraalissa sääntöä 1 sovelletaan, koska se on K = 7:

∫7dx = 7∫dx = 7x + c₂

Ja nyt tulokset lisätään. Kaksi vakiota on ryhmitelty yhdeksi, yleisesti nimeltään C:

∫ (x+7) dx = (x² /2) + 7x + c

Ratkaisu b

Lineaarisuudella tämä integraali hajoaa kolmeen yksinkertaisempaan integraaliin, joihin sovelletaan valtuuksien sääntöä:

∫ (x^3/2 + x² + 6) dx = ∫x^3/2 Dx + ∫x² dx +∫6 dx =

= (2/5) x^5/2 + (1/3) x³ + 6x + c

Huomaa, että jokaisesta integraalista integraatiovakio ilmestyy, mutta ne kokoontuvat yhdessä puhelussa C.

Liuos C

Tässä tapauksessa on kätevää soveltaa kertolaskun jakautuvaa ominaisuutta integroivan kehittämiseksi. Sitten käytät valtuuksien sääntöä löytääksesi jokaisen integraalin erikseen, kuten edellisenä vuonna.

∫ (x+1) (3x-2) dx = ∫ (3x²-2x+3x-2) dx = ∫ (3x² + X - 2) dx

Huomaavainen lukija huomauttaa, että nämä kaksi keskeistä termiä ovat samanlaiset, siksi ne vähenevät ennen integrointia:

∫ (x+1) (3x-2) dx = ∫3x² dx + ∫ x dx + ∫- 2 dx = x³ + (1/2) x² - 2x + c

Ratkaisu E

Tapa ratkaista integraali olisi voiman kehittäminen, kuten esimerkissä D tehtiin. Koska eksponentti on korkeampi, olisi tarpeen tehdä muuttuja muutos, jotta ei tarvitse tehdä niin pitkää kehitystä.

Voi palvella sinua: jatkuva satunnaismuuttuja

Muuttujan muutos on seuraava:

U = x + 7

Johdetaan molemmille puolille tämä lauseke:

du = dx

Integraali muuttuu yksinkertaisemmaksi uuden muuttujan kanssa, joka on ratkaistu voimansääntöllä:

∫ (x+7)⁵ Dx = ∫ u⁵ du = (1/6) u⁶ + C

Lopuksi muutos palautetaan palaamaan alkuperäiseen muuttujaan:

∫ (x+7)⁵ Dx = (1/6) (x+7)⁶ + C

- Harjoitus 2

Hiukkas on alun perin levossa ja liikkuu X -akselia pitkin. Sen kiihtyvyys T> 0: lle annetaan funktiolla a (t) = cos t. Tiedetään, että t = 0, sijainti on x = 3, kaikki kansainvälisen järjestelmän yksiköissä. Hiukkasen nopeutta v (t) ja sijainti x (t) löydät nopeutta v (t) ja.

Ratkaisu

Koska kiihtyvyys on ensimmäinen nopeudesta ajankohtana, sinulla on seuraava differentiaaliyhtälö:

a (t) = v '(t) = cos t t

Seuraa, että:

v (t) = ∫ cos t dt = sin t + c₁

Toisaalta tiedämme, että nopeus on puolestaan ​​aseman johdannainen, siksi integroitumme uudelleen:

x (t) = ∫ v (t) dt = ∫ (sin t + c₁) dt = ∫sen t dt + ∫c₁ dt = - cos t + c₁ t + c₂

Integraatiovakiot määritetään lausunnossa annettujen tietojen perusteella. Ensinnäkin hän sanoo, että hiukkas oli alun perin levossa, siksi v (0) = 0:

V (0) = sin 0 + c₁ = 0

C₁ = 0

Sitten sinun täytyy x (0) = 3:

x (0) = - cos 0 + c₁ 0 + c₂ = - 1 + C₂ = 3 → C₂ = 3+1 = 4

Nopeus- ja sijaintitoiminnot ovat ehdottomasti tällaisia:

v (t) = sen t

x (t) = - cos t + 4

Viitteet

1. Engler, a. 2019. Kiinteä laskenta. Rannikon kansallinen yliopisto.
2. Larson, r. 2010. Muuttujan laskenta. 9NA. Painos. McGraw Hill.
3. Ilmaiset matematiikan tekstit. Antiderivatiivi. Toipunut: matematiikka.Libretext.org.
4. Wikipedia. Ykkös-. Haettu: vuonna.Wikipedia.org.
5. Wikipedia. Määrittelemätön integraatio. Palautettu: on.Wikipedia.org.