Archimedes -periaatteen kaava, esittely, sovellukset

Hän Archimedesin periaate Hän sanoo, että täysin tai osittain upotettu elin saa pystysuoran voiman nimeltään työntää, joka vastaa rungon syrjäyttämän nesteen tilavuuden painoa. 

Jotkut esineet kelluvat vedessä, toiset uppoutuvat ja jotkut osittain upottavat itsensä. Rantapallojen upottamiseksi on tarpeen yrittää, koska tämä voima havaitaan heti, joka yrittää palauttaa sen pintaan. Sen sijaan metallipallo uppoaa nopeasti. 

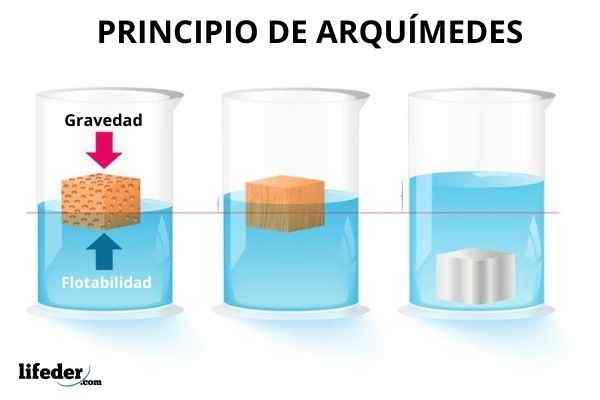
Toisaalta, upotetut esineet vaikuttavat kevyemmiltä, ​​joten paino, joka on painostava neste, on voimassa. Mutta et voi aina kompensoida ollenkaan painovoimaa. Ja vaikka se käy ilmi vedestä, kaasut kykenevät myös tuottamaan tämän voiman upotettuihin esineisiin.

[TOC]

Historia

Syracusen arkimeja (287-212 a. C.) Se oli se, joka oli pitänyt löytää tämä periaate, joka on yksi historian suurimmista tutkijoista. He sanovat, että Syrakusan kuningas Hierón II lähetti kultasepän uuden kruunun valmistamiseen, jolle hän antoi hänelle tietyn määrän kultaa.

Arkkitehtuuri

Kun kuningas sai uuden kruunun, hänellä oli oikea paino, mutta hän epäili, että kultaseppä oli pettänyt häntä lisäämällä hopeaa kullan sijasta. Kuinka voisin tarkistaa sen tuhoamatta kruunua?

Hierón nimeltään Archimedes, jonka tutkijan kuuluisuus oli hyvin tunnettu, auttamaan häntä ratkaisemaan ongelman. Legenda vakuuttaa, että Archimedes oli upotettu kylpyammeeseen, kun hän löysi vastauksen ja sellainen oli hänen tunteensa, että hän juoksi alasti Syrakusan kaduilla etsimään kuningasta huutaen "Eureka", mikä tarkoittaa "löysin sen".

https: // giphy.com/gifs/stito3echtlnbvliz3

Mitä arkimoidut löysivät? No, kun kylpyhuonetta otetaan kylpyhuoneessa, kun hän tuli sisään, mikä tarkoittaa, että upotettu runko syrjäyttää tietyn nesteen määrän.

Ja jos upotin kruunun veteen, sen oli myös siirrettävä tiettyä vettä vettä, jos kruunu olisi valmistettu kullasta ja erilainen, jos se tehtiin seoksesta hopealla.

Archimedes -periaatteen kaava

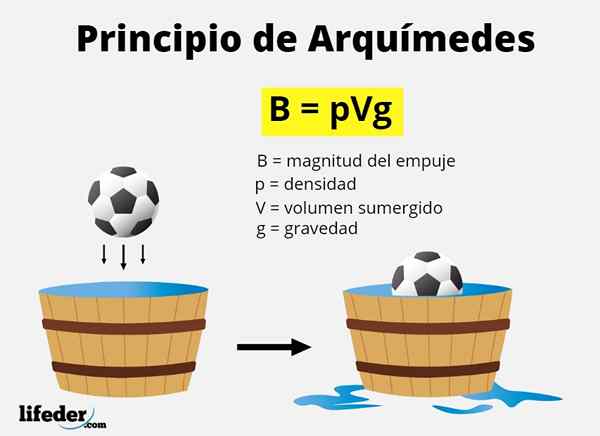
Archimedes -periaatteessa tarkoitettu mainosjoukko tunnetaan nimellä työntää hydrostaattinen jompikumpi vaahdotusvoima Ja kuten olemme sanoneet, se vastaa kehon siirtämän nesteen tilavuuden painoa upotettuna.

Siirtymätilavuus vastaa upotettua objektin äänenvoimakkuutta, joko kokonaan tai osittain. Koska kaiken paino on mg, Ja nesteen massa on Tiheys x tilavuus, Kieltäytyy kuinka b työntövoiman suuruuteen, matemaattisesti sen on:

B = m_sujuva x g = nesteen tiheys x upotettu tilavuus x painovoima

B = ρ_sujuva X V_upotettu x g

Missä kreikkalainen kirjain ρ ("Rho") tarkoittaa tiheyttä.

Näennäinen paino

Objektien paino lasketaan hyvin tunnettulla lausekkeella mg, Asiat tuntuvat kuitenkin kevyemmiltä, ​​kun ne upotetaan veteen. 

Hän näennäinen paino esineestä on se, mitä se on upotettu veteen tai muuhun nesteeseen ja tietäen sen, voit saada epäsäännöllisen esineen, kuten kuninkaan hierónin kruunun, tilavuuden, kuten alla näkyy.

Voi palvella sinua: 13 esimerkkiä Newtonin ensimmäisestä laista tosielämässä

Tätä varten se on täysin upotettu veteen ja altistuu köyden kiinnitettyyn köyteen dynamometri -instrumentti, joka on varustettu jousella, joka palvelee voimien mittaamista-. Mitä suurempi esineen paino on, sitä suurempi jousen venymä, joka mitataan laitteessa toimitetulla asteikolla.

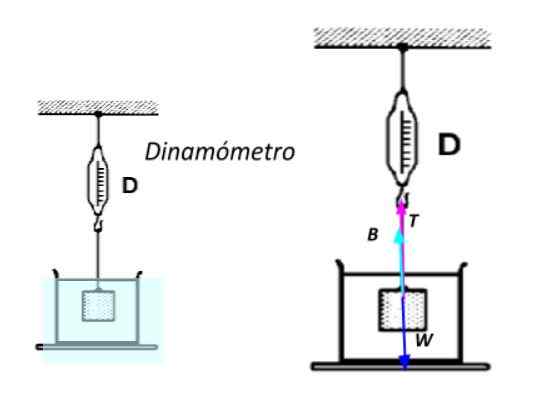Upotetun esineen näennäinen paino. Lähde: valmistettu f. Zapata.

Newtonin toisen lain soveltaminen tietäen, että esine on levossa:

Σf_ja = B + t - w = 0

Näennäinen paino w_-lla Se vastaa T -köyden jännitystä:

T = w_-lla

W -_-lla = mg - ρ_sujuva . V. g

Jos upotettu osa V vaaditaan, se puhdistetaan seuraavasti:

V = (w - w_-lla ) / ρ_sujuva  . g

Esittely

https: // giphy.com/gifs/mcppppgtnpbhl4cgaq

Kun vartalo uppoutuu, työntövoima on voima, joka johtuu kaikista vartaloon kohdistuvista voimista ympäröivän nesteen aiheuttaman paineen kautta:

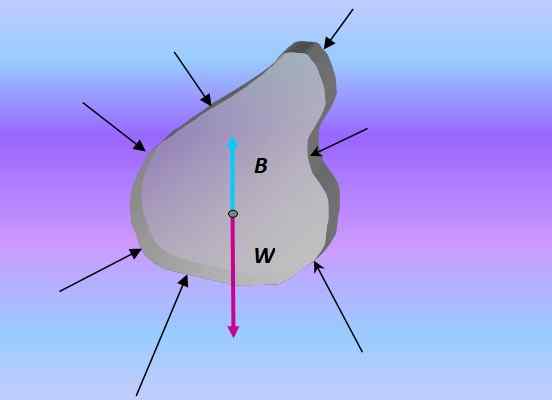Vapaa kehon kaavio upotetusta esineestä. Lähde: valmistettu f. Zapata.

Paine ja syvyys

Koska paine kasvaa syvyyden myötä, näiden voimien tulos on aina suunnattu pystysuoraan ylöspäin. Siksi Archimedes -periaate on seuraus hydrostaattisen peruslauseen, joka liittyy nesteen kohdistaman paine P: n syvyyteen P -paineen P z -z kuten:

P = ρ.g.z -z

Voimat staattisen tasapainon nesteessä

Archimedes -periaatteen osoittamiseksi otetaan pieni lieriömäinen lepoosuus, joka analysoidaan siihen käytettyihin voimiin, kuten seuraavassa kuvassa esitetään. Sylinterin kaarevan pinnan voimat peruutetaan toistensa kanssa. 

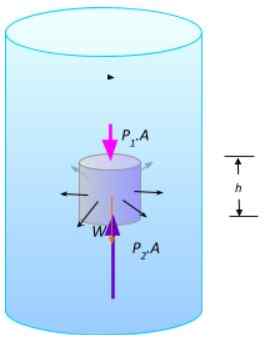Osa nestettä tasapainossa. Lähde: valmistettu f. Zapata.

Pystysuorien voimien suuruudet ovat F₁ = P₁.A ja F₂ = P2.A, on paino W -. Koska neste on tasapainossa, voimien summa on peruutettava:

∑f_ja = P₂.A-p₁.A- w = 0

P₂.A-p₁.A = w

Koska työntövoima kompensoi painon, koska nesteen osa on levossa, niin:

B = P₂.A-p₁.A = w

Tästä lausekkeesta seuraa, että työntövoima johtuu sylinterin yläpinnan ja alemman paineen erosta. Kuten W = mg = ρsujuva. V. g, Sinun täytyy:

B = ρ_sujuva. V_upotettu. g

Joka on juuri edellisessä osassa mainitun työntövoiman ilmaisu.

Archimedes -periaatteelliset hakemukset

Kelluvat ilmapallot: Archimedes -periaate toiminnassa

Archimedes -periaate esiintyy monissa käytännön sovelluksissa, joista voimme nimetä:

- Aerostaattinen ilmapallo. Joka on keskimäärin tiheys pienempi kuin ympäröivän ilman tiheys, kelluu siinä työntövoiman takia.

- Laivat. Laivan kypärä on raskaampi kuin vesi. Mutta jos rungoa pidetään sekä ilmaa sisäpuolella, kokonaismassan ja tilavuuden välinen osuus on pienempi kuin veden ja siksi alukset kelluvat.

- Pelastusliivit. Kun ne on rakennettu valosta ja huokoisista materiaaleista, ne kykenevät kellumaan, koska massan tilavuussuhde on pienempi.

- Kellu sulje vesisäiliön täyttönauha. Se on pallo, joka on täynnä veden yli kelluvan suuren tilavuuden ilmaa, joka aiheuttaa työntövoiman - kerrottuna vipuvaikutuksella - sulkee vesisäiliön täyttönauhan korkin, kun se on saavuttanut tason kokonaismäärän.

Se voi palvella sinua: yksidimensionaaliset aallot: matemaattinen ilmaisu ja esimerkit

Esimerkit

Esimerkki 1

Legenda kertoo, että kuningas Hierón antoi kultasepään tietyn määrän kultaa kruunun tekemiseen, mutta epäluotettava hallitsija ajatteli, että kultaseppä olisi voinut huijata asettaessaan vähemmän arvokasta metallia kruunun sisään kuin kruunu. Mutta miten voin tietää tuhoamatta kruunua? 

Kuningas tilasi Archimedesin ja tämän ratkaisun etsimisen, löysi hänen kuuluisan periaatteensa.

Oletetaan. Tässä tapauksessa petoksia ei ole?

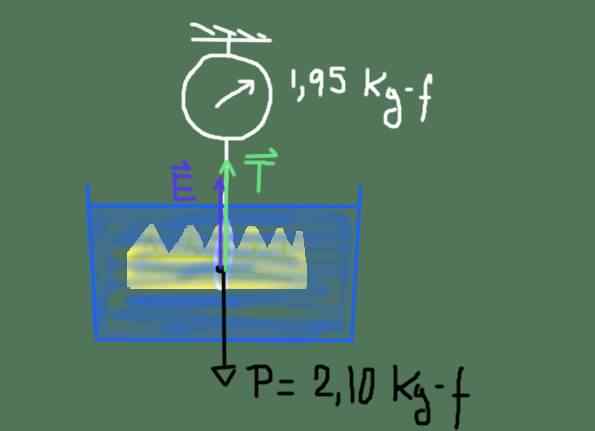Kuningas Heronin kruunuvapaa ruumiskaavio. Lähde: valmistettu f. Zapata

Voiman kaavio on esitetty edellisessä kuvassa. Nämä voimat ovat: paino P kruunun, työntövoiman JA ja jännitys T asteikosta roikkuvasta köydestä.

P = 2,10 kg-F ja T = 1,95 kg-F tunnetaan, on välttämätöntä määrittää työntövoiman suuruus JA-

T + e = p ⇒ e = p - t = (2,10 - 1,95) kg -f = 0,15 kg -f

Toisaalta Archimedes -periaatteen mukaan työntövoima vastaa kruunun käyttämän tilan häätetyn veden painoa, ts. Veden tiheys kruunun tilavuudella johtuen painovoiman kiihtyvyydestä johtuen painovoimasta -

E = ρ_vettäMuus

Missä kruunun tilavuus voidaan laskea:

V = 0,15 kg / 1000 kg / m^3 = 0,00015 m^3

Kruunun tiheys on kruunun massan ja sen tilavuuden välinen osoitus:

Kruunun tiheys = 2,10 kg / 0,00015 m^3 = 14000 kg / m^3

Puhtaan kullan tiheys voidaan määrittää samanlaisella menettelyllä ja tulos on 19300 kg/m^3.

Vertaamalla kahta tiheyttä on selvää, että kruunu ei ole puhdasta kultaa! 

Esimerkki 2 

Tietojen ja esimerkin 1 tuloksen perusteella on mahdollista määrittää, kuinka paljon kultaa kultaseppä varasti siinä tapauksessa, että kullan osa on korvattu hopealla, jonka tiheys on 10500 kg/m^3 3 3 3.

Kutsumme ρc: n kruunun tiheyteen, ρo kullan ja ρ: n tiheyteen_p hopean tiheyteen.

Kruunun kokonaismassa on:

M = ρc⋅V = ρo⋅vo + ρ_p⋅VP

Kruunun kokonaistilavuus on hopean tilavuus plus kullan tilavuus:

V = vo + vp ⇒ vp = v - vo

Massayhtälön korvaaminen:

ρc⋅V = ρo⋅vo + ρ_p⋅ (v - vo) ⇒ (ρo - ρ_p) Vo = (ρc - ρ_p) V

Toisin sanoen kullan tilavuus, joka sisältää kokonaismäärän V kruunun V: on:

VO = v⋅ (ρc - ρ_p)/(ρo - ρ_p) =…

… = 0,00015 m^3 (14000 - 10500)/(19300 - 10500) = 0,0000596 m^3

Kultaisen painon tuntemiseksi, joka sisältää kruunun, kerrotaan VO kullan tiheyden vuoksi:

Voi palvella sinua: oikeanpuoleinen sääntö

MO = 19300 *0,00005966 = 1,1514 kg

Koska kruunun massa on 2,10 kg, tiedämme, että kultaseppä varasti 0,94858 kg kultaa ja korvattiin hopealla.

Ratkaisut

Harjoitus 1

Valtava heliumpallo pystyy ylläpitämään tasapainossa (nousematta tai laskeutumista) henkilölle.

Oletetaan, että ihmisen paino sekä kori, jouset ja ilmapallo on 70 kg. Mikä on heliumin tilavuus, jotta tämä tapahtuu? Minkä kokoisella ilmapallolla on?

Ratkaisu

Oletetaan, että työntövoima tuottaa pääasiassa heliumin tilavuus ja että muiden komponenttien työntövoima on hyvin pieni verrattuna heliumin, joka vie paljon enemmän tilavuutta.

Tässä tapauksessa heliumtilavuus vaaditaan tarjoamaan 70 kg + painon työntövoiman.

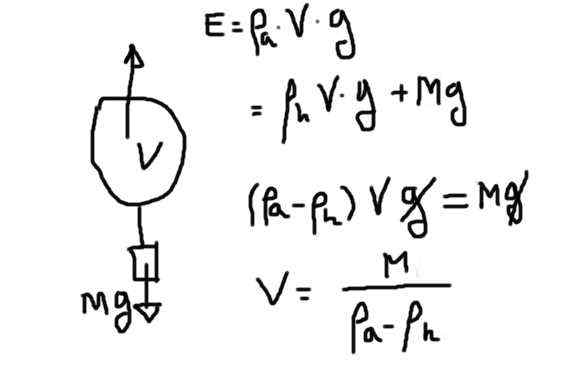Vapaa kehon fdiaogrammi täynnä heliumia. Lähde: valmistettu f. Zapata.

Työntövoima on heliumin tilavuuden tuote, joka johtuu heliumin tiheydestä painovoiman kiihtyvyyden vuoksi. Tämän työntövoiman on kompensoitava heliumin paino sekä muiden paino.

Da⋅V⋅g = da⋅V⋅g + m⋅g

missä se päättelee, että v = m / (da - dh)

V = 70 kg / (1.25 - 0,18) kg/m^3 = 65.4 m^3

Eli 65 vaaditaan.4 m^3 heliumia ilmakehän paineessa tukea.

Jos oletamme pallomaisen ilmapallon, voimme löytää saman säteen pallon säteen ja säteen välisestä suhteesta:

V = (4/3) ⋅π⋅r^3

Missä r = 2,49 m. Toisin sanoen vaaditaan 5 m halkaisija, joka on täynnä heliumia.

Harjoitus 2

Alempi tiheysmateriaalit, jotka veden kelluvat samassa. Oletetaan, että sinulla on polystyreenikuutioita (valkoinen korkki), puu ja jää. Hänen tiheytensä kg kuutiometriä kohti ovat vastaavasti: 20, 450 ja 915.

Selvitä, mikä osuus kokonaistilavuudesta on vedestä ja mikä korkeus erottuu veden pinnan suhteen viimeksi mainitun 1000 kilogramman tiheytenä kuutiometriä kohti.

Ratkaisu 

Kelluvuus tapahtuu, kun kehon paino on yhtä suuri kuin vedestä johtuva työntövoima:

E = m⋅g

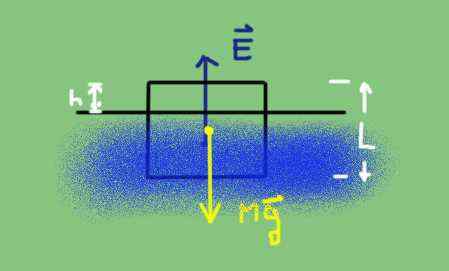Vapaa kehon kaavio osittain upotetusta esineestä. Lähde: valmistettu f. Zapata.

Paino on kehon tiheys tasavirtaan kerrottuna sen tilavuudella V ja painovoiman kiihtymisellä G.

Työntövoima on syrjäytyneen nesteen paino Archimedes -periaatteen mukaisesti ja se lasketaan kertomalla veden tiheys D upotetulla tilavuudella V 'ja painovoiman kiihtymisellä.

Tuo on:

D⋅V'⋅g = Dc⋅V⋅g

Mikä tarkoittaa, että upotettu tilavuusosuus on yhtä suuri kuin kehon tiheyden ja veden tiheyden välinen osuus.

(V '/V) = (DC/D) 

Toisin sanoen erinomainen tilavuusosuus (v "/v) on

(V "/V) = 1 - (DC/D)

Joo h Se on erinomainen korkeus ja Lens Kuution puoli äänenvoimakkuuden osuus voidaan kirjoittaa

(H⋅l^2)/(l^3) = h/l, Toisin sanoen myös erinomainen korkeusosa on

(H/L) = 1 - (DC/D)

Sitten pyydettyjen materiaalien tulokset ovat:

Polystyreeni (valkoinen korkki):

(H/L) = (V "/V) = 1 - (DC/D) = 1- (20/1000) = 98% vettä

Puu:

(H/L) = (V "/V) = 1 - (DC/D) = 1- (450/1000) = 55% vettä

Jää:

(H/L) = (V "/V) = 1 - (DC/D) = 1- (915/1000) = 8.5% vettä

Viitteet

1. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill. 417-455.
2. Cengel Y, Cimbala J. 2011.Fluidimekaniikka. Perusteet ja sovellukset. Ensimmäinen painos. McGraw Hill.
3. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Osa 4. Nesteet ja termodynamiikka. Toimittanut Douglas Figueroa (USB). 1 - 42.
4. Giles, r. 2010. Neste- ja hydraulinen mekaniikka. McGraw Hill. 
5. Rex, a. 2011. Fysiikan perusteet. Pearson. 239-263.
6. Tippens, P. 2011. Fysiikka: Käsitteet ja sovellukset. 7. painos. McGraw Hill.