Pääsiäisen periaatteen historia, sovellukset, esimerkit

Hän Pascal -periaate, o Pascal -laki toteaa, että mihin tahansa sen pisteeseen rajoitetun nesteen paineen muutos siirtyy ilman muutoksia kaikkiin muihin nesteen kohtiin liittyviin pisteisiin.

Tämän periaatteen löysi ranskalainen tutkija Blaise Pascal (1623 - 1662). Pascalin tieteen antamien panosten merkityksen vuoksi kansainvälisen järjestelmän paineyksikkö on nimitetty sen kunniaksi.

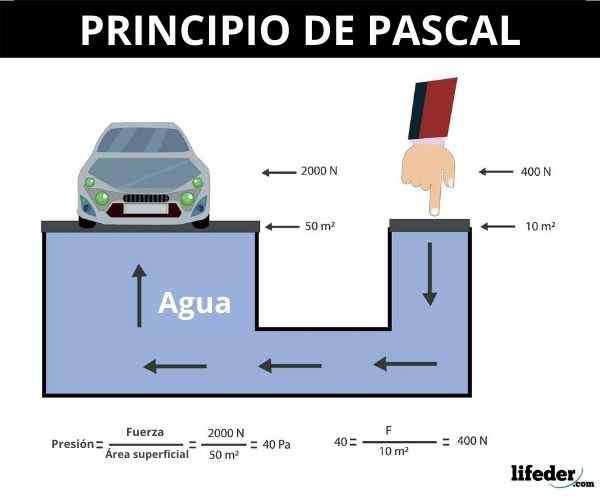
Koska paine on määritelty osamääräksi kohtisuorassa alueen välillä, 1 Pascal (PA) on 1 Newton / M².

[TOC]

Historia

Pascal suunnitteli sen periaatteensa tarkistamiseksi melko ylivoimaisen mielenosoituksen. Hän otti ontto pallon ja lävisti useissa paikoissa, laitti korkit kaikkiin reikiin paitsi yhdessä, josta hän täytti sen vedellä. Tässä hän asetti ruiskun, joka on annettu männällä.

Lisäämällä riittävästi männän painetta, korkit ammutaan samanaikaisesti, koska paine siirtyy tasa -arvoisesti kaikkiin nesteen kohtiin ja kaikkiin suuntiin, mikä osoittaa Pascal -lakia.

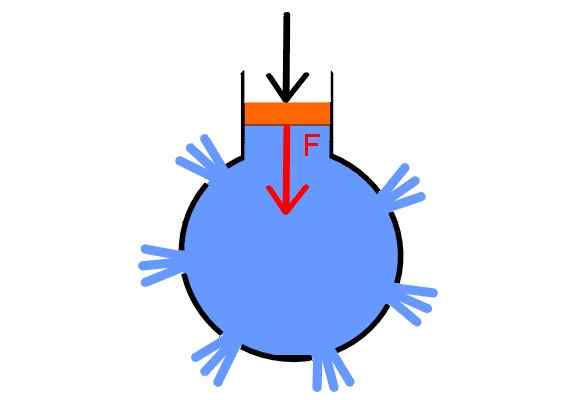Pascal -ruisku. Lähde: Wikimedia Commons.

Blaise Pascalilla oli lyhyt elämä, tauti leimaa. Hänen mielensä uskomaton ulottuvuus sai hänet tutkimaan luonnon ja filosofian eri näkökohtia. Hänen panoksensa ei rajoittunut nesteiden käyttäytymisen tutkimiseen, Pascal oli myös tietojenkäsittelyn edelläkävijä.

Ja 19 -vuotiaana Pascal loi isänsä mekaanisen laskimen käyttää häntä työssään Ranskan verojärjestelmässä: Pascalina.

Myös ystävänsä ja kollegan kanssa Ferman suuren matemaatikon Pierre muodosti todennäköisyyden teorian, välttämätöntä fysiikassa ja tilastoissa. Pascal kuoli Pariisissa, 39 -vuotiaana.

Selitys Pascal -periaatteesta

Seuraava koe on melko yksinkertainen: U -putki on täytetty vedellä ja kumpaankin päähän asetetaan korkit, jotka voivat liukua sujuvasti ja helposti, mäntänä. Se on paine vasemman männän suhteen, joka uppoaa hiukan ja havaitaan, että oikealla oleva nousee, nesteen työntämä (alempi kuva).

Voi palvella sinua: Andromeda: löytö, alkuperä, ominaisuudet, rakenne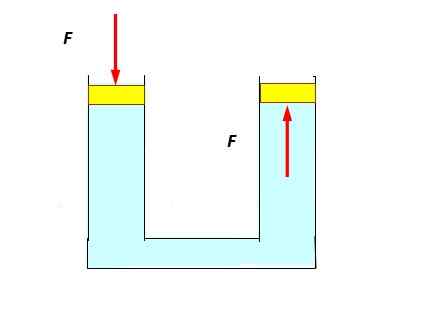Pascal -periaatteen soveltaminen. Lähde: Itse tehty.

Näin tapahtuu, koska paine siirretään ilman nesteen kokonaispistettä, mukaan lukien ne, jotka ovat kosketuksissa oikean männän kanssa.

Nesteet, kuten vesi tai öljy.

Tämän ansiosta oikea mäntä vastaanottaa voiman, joka on täsmälleen sama suuruudessa ja suunnassa, johon se levitettiin vasemmalle, mutta vastakkaisesta suunnasta.

Paine staattisessa nesteessä on riippumaton säiliön muodosta. Välittömästi osoitetaan, että paine vaihtelee lineaarisesti syvyyden ja Pascalin periaatteen mukaan.

Paineen muutos missä tahansa vaiheessa tekee paineen toisessa pisteessä muuttuvan samassa määrässä. Muuten olisi ylimääräinen paine, joka virtaa nestettä.

Paineen ja syvyyden välinen suhde

Lepo -neste kohdistaa sen sisältävän astian seinämiin ja myös siihen upotetun esineen pinnalle. Pascal -ruiskun kokeessa nähdään, että vesi roiske tulee ulos kohtisuorasti Pallo.

Nesteet jakavat voiman kohtisuorassa pinnalle, jolla se toimii, joten on kätevää ottaa käyttöön keskimääräinen paineen käsite P_m kohtisuorassa voimana kohdistuessa F_⊥ Alueen mukaan -Lla, Kenen yksikkö on Pascal:

P_m = F_⊥ /

Paine kasvaa syvyyden myötä. Voit nähdä pienen osan staattisesta tasapainosta ja soveltaa Newtonin toista lakia:

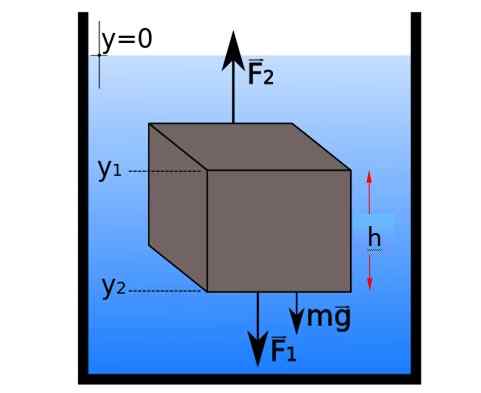Vapaa runkokaavio pienestä staattisen tasapainon osasta, jossa on kuutiokuutio. Lähde: E-Xuao [CC BY-SA 4.0 (https: // creativecommons.Org/lisenssit/by-SA/4.0)]

Vaakavoimat peruutetaan pareilla, mutta pystysuunnassa joukot ryhmitetään seuraavasti:

∑f_ja = F₂ - F₁ - Mg = 0 → F₂ - F₁ = mg

Taikinan ilmaiseminen tiheyden suhteen ρ = massa /tilavuus:

P₂.A-p₁.A = ρ X Volume x g

Nesteen osan tilavuus on tuote x H: n:

Se voi palvella sinua: termodynamiikan toinen laki: kaavat, yhtälöt, esimerkit

-Lla.(P₂ - P₁) = ρ X a x h x g

ΔP = ρ.g.h   Hydrostaattisen peruslause

Sovellukset

Backhegoe käyttää Pascal -periaatetta suurten pesojen nostamiseen

Pascal -periaatetta on käytetty rakentamaan lukuisia laitteita, jotka kertovat lujuuteen ja helpottamaan tehtäviä, kuten peson nostaminen, metallin leimaaminen tai esineiden puristaminen. Heidän joukossaan ovat:

-Hydraulinen puristus

-Autojarrujärjestelmä

-Mekaaniset lapiot ja mekaaniset aseet

-Hydraulinen kissa

-Nosturit ja hissit

Seuraavaksi katsotaan, kuinka Pascal -periaate saa pienet voimat muuttumaan suuriksi voimiksi suorittamaan kaikki nämä teokset. Hydraulinen puristus on ominaisten esimerkki, ja se analysoidaan alla.

Hydraulinen puristus

Hydraulisen puristimen rakentamiseksi otetaan sama ylemmän kuvan laite, ts. U -muotoinen säiliö, jonka tiedämme jo, että sama voima lähetetään yhdestä männästä. Ero on mäntien koko ja tämä saa laitteen toimimaan.

Seuraava kuva näyttää Pascal -periaatteen toiminnassa. Paine on sama nesteen kaikissa kohdissa, sekä pienessä että suuressa männässä:

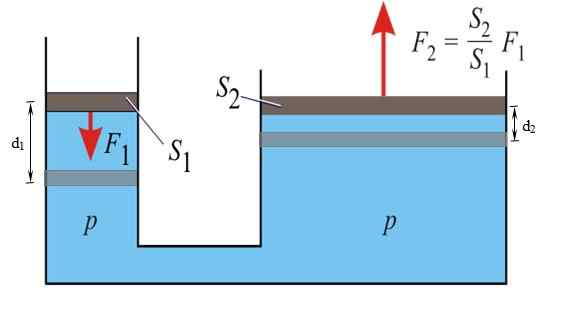Hydraulinen puristusjärjestelmä. Lähde: Wikimedia Commons.

p = f₁ / S₁ = F₂ / S₂

Suurelle männään siirrettävän voiman suuruus on:

F₂ = (S₂ / S₁-A. F₁

Kuin s₂ Sose₁, Tulokset F: ssä₂ > F₁, Siksi poistumisvoima on moninkertaistunut tekijässä, joka on annettu alueiden välillä.

Esimerkit

Tämä osa näyttää sovellusesimerkkejä.

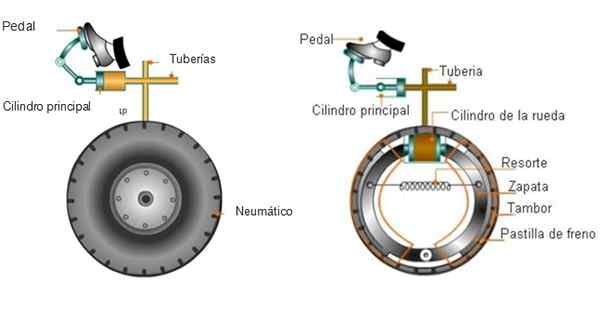
Hydrauliset jarrut

Auton jarrut käyttävät Pascal -periaatetta hydraulisen nesteen kautta, joka täyttää joitain pyöriin kytkettyjä putkia. Kun sinun on lopetettava, kuljettaja käyttää voimaa sortamalla jarrupoljinta ja aiheuttamalla nesteen painetta.

Toisessa päässä paine työntää jarrutyynyjä rumpu- tai jarrulevyjä vasten, jotka kääntyvät pyörien kanssa (ei renkaiden kanssa). Tuloksena oleva kitka saa levyn pysähtymään, hidastaen myös pyöriä.

Voi palvella sinua: mekaaniset aallot: ominaisuudet, ominaisuudet, kaavat, tyypitHydraulinen jarrujärjestelmä. Lähde: f. Zapata

Hydraulisen puristimen mekaaninen etu

Alemman kuvan hydraulisessa puristimessa sisäänkäynnin on oltava yhtä suuri kuin poistumistyö, kunhan kitka ei oteta huomioon.

Syöttövoima F₁ saa mäntä matkustamaan etäisyyden d₁ Kun menet alas, ollessa poistumisvoima F₂ Sallii d₂ männästä, joka nousee. Jos molempien voimien tekemä mekaaninen työ on sama:

F₁.d -d₁ = F₂. d -d₂

Mekaaninen etu m on osamäärä syöttö- ja lähtövoiman suuruuksien välillä:

M = f₂/F₁ = D₁/D₂

Ja kuten edellisessä osassa osoitetaan, se voidaan ilmaista myös alueiden välisenä osana:

F₂/F₁ = S₂ / S₁

Vaikuttaa siltä, ​​että työ tehdään ilmaiseksi, mutta se ei oikeastaan ​​luo energiaa tämän laitteen kanssa, koska mekaaninen etu saadaan pienen männän siirtymän kustannuksella₁.

Joten suorituskyvyn optimoimiseksi venttiilijärjestelmä lisätään laitteeseen siten, että lähtö mäntä nostetaan tulossarjan lyhyiden impulssien ansiosta.

Tällä tavoin autotalli hydraulisen kissan pumppaa useita kertoja ajoneuvon asteittain nostamiseksi.

Liikuntaa

Kuvan 5 hydraulisessa puristimessa mäntien alueet ovat 0.5 neliötuumaa (pieni mäntä) ja 25 neliötuumaa (iso mäntä). Löytö:

a) Tämän puristimen mekaaninen etu.

b) tarvittava voima 1 tonnin kuorman nostamiseksi.

c) Etäisyys, jolla sisäänkäynnin voiman on toimittava mainittu kuorma 1 tuumaa.

Ilmaise kaikki tulokset brittiläisen järjestelmän ja kansainvälisen järjestelmän yksiköissä.

Ratkaisu

a) Mekaaninen etu on:

M = f₂/F₁ = S₂/S₁ = 25 tuumaa² / 0.5 tuumaa² = 50

b) 1 tonnia, joka vastaa 2000 lb-voimaa. Tarvittava vahvuus on f₁-

F₁ = F₂ / M = 2000 lb-voima / 50 = 40 lb-voima

Tuloksen ilmaisemiseksi kansainvälisessä järjestelmässä vaaditaan seuraava muuntokerroin:

1 lb-force = 4.448 n

Siksi F1: n suuruus on 177.92 n.

c) M = D₁/D_{2 →} d -d₁ = M.d -d₂ = 50 x 1 in = 50 tuumaa

Tarvittava muuntokerroin on: 1 in = 2.54 cm

d -d₁ = 127 cm = 1.27 m

Viitteet

1. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill. 417-450.
2. Korkeakoulufysiikka. Pascalin periaattori. Palautettu: OpenTextbc.Ac.
3. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Osa 4. Nesteet ja termodynamiikka. Toimittanut Douglas Figueroa (USB). 4 - 12.
4. Rex, a. 2011. Fysiikan perusteet. Pearson. 246-255.
5. Tippens, P. 2011. Fysiikka: Käsitteet ja sovellukset. 7. painos. McGraw Hill.301-320.