Fyysinen

Voimien periaate siirrettävyys

Voimien periaate siirrettävyys

Selitämme, mikä on siirrettävyyden periaate, esimerkkejä ja harjoituksia ratkaistaan

Mikä on lähetettävyysperiaate?

Hän Siirrettävyysperiaate Se koskee kiinteitä esineitä ja vahvistaa, että kehon jossain kohdassa käytetty voima vastaa toista yhtä suurta ja suuntaa yhtä suurta voimaa, kunhan mainittu voima kohdistuu samaan viivaan, joka sisältää alkuperäiseen voimaan.

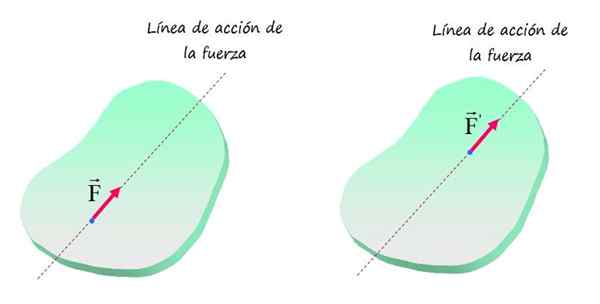
Siksi mikä tahansa saman suuruuden ja suunnan voima aiheuttaa objektin saman vaikutuksen saman vaikutuksen, edellyttäen, että sen käyttöpiste sijaitsee samalla viivalla, kuten seuraavassa kuvassa esitetään.

Jäykällä rungossa voiman vaikutusta ei muuteta, kun sen levityspiste liikkuu sen toimintalinjaa pitkin. Lähde: f. Zapata.

Näytetyt voimat F ja F'Sanotaan, että he ovat vastaavat voimat ja niitä sisältävää äkillistä suoraa linjaa kutsutaan voimansiirto.

Siirrettävyysperiaate on erittäin hyödyllinen, koska se sallii mukavuuden kohteena objektille toimivia voimia analyysin helpottamiseksi.

Selitys jstk Siirrettävyysperiaate

Siirrettävyysperiaate perustuu siihen, että kaksi voimaa F1 ja F2 Ne ovat vastaavia, sillä ehdolla, että heillä on sama ja sama suunta.

Lisäksi niiden on tuotettava sama hetki mihin tahansa kohtaan tai, mikä taataan samalla, että sillä on sama toimintalinja ja koska hetki on voiman tuote etäisyyden kautta tai mainitun linjan kautta.

Huomaa, että periaatetta sovelletaan vain jäykään runkoon, toisin sanoen esineeseen, jossa niiden osien väliset suhteelliset etäisyydet eivät muutu, koska sen sisäiset voimat ovat riittävän voimakkaita. Siksi esine ei muokkaa muotoa riippumatta siitä, toimivatko nämä ulkoiset voimat siihen vai ei.

Toisaalta, jos objekti ei ole jäykkä, voimien levityskohdan muuttaminen tuottaisi variaatioita kehoon käytetyn jännityksen tai puristuksen suhteen, mikä johtaisi sen muodon muutoksiin.

Oletetaan tietysti, että vartalo on jäykkä ei ole muuta kuin idealisointi, koska todellisuudessa kaikki esineet ovat muodonmuutoksia suuremmassa tai pienemmässä määrin. Monissa tapauksissa se on kuitenkin erinomainen lähestymistapa, jos muodonmuutos on riittävän pieni, jotta sitä voidaan pitää halveksittavana.

Rajoitukset

Siirrettävyysperiaate on, kuten osoitettu, rajoitukset ampumisen tai voimien liukumisen suhteen. Seuraavassa kuvassa esitetään esine, jolla on voimat F ja F'sovelletaan saman toimintalinjan eri kohtiin.

Voi palvella sinua: Archimedes Periaate: Kaava, esittely, sovellukset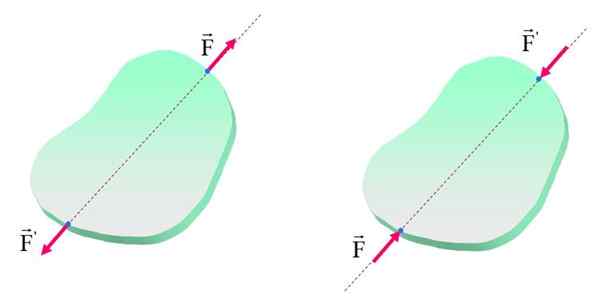Siirrettävyysperiaatetta sovelletaan vain jäykillä kappaleilla, koska voimien levityspisteen muuttaminen voi aiheuttaa erilaisia ​​vaikutuksia muodonmuutosrunkoihin. Lähde: f. Zapata.

Huomaa, että molemmissa kuvioissa runko (jäykkä tai ei) on tasapainossa, koska voimilla on yhtä suuruus ja suunta ja vastakkaiset aistit. Lisäksi voimat ovat, kuten on sanottu, samalla toimintalinjalla, mutta vasemmassa kuvassa vaikutus kehoon on jännitys, kun taas oikealla vaikutus on puristus.

Siksi, vaikka vartalo pysyy levossa, sisäiset vaikutukset ovat erilaisia ​​ja niistä tulee patenttia, jos esine ei ole täysin jäykkä. Vasemman tapauksessa voimat pyrkivät pidentämään vartaloa, kun taas oikealla heillä on taipumus lyhentää sitä.

Esimerkkejä Siirrettävyysperiaate

Esimerkki 1

Oletetaan, että vaakasuorassa lattialla on raskas tavara. Sen vaikutukset vasemmalle puolelle on sama kuin jos se olisi tasainen. Tässä tapauksessa tavaratilan liike maassa on sama.

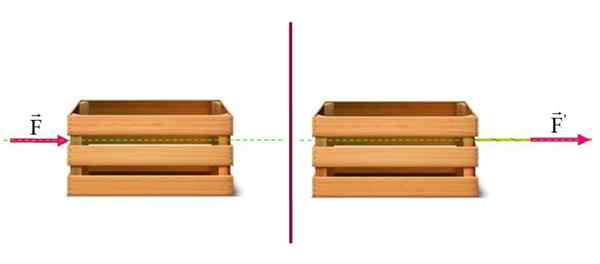Laatikon työntämisen tai vetämisen vaikutus vaakasuoraan pintaan on sama: Siirrä sitä vasemmalta oikealle. Lähde: f. Zapata.

Esimerkki 2

Sinulla on pitkä lankku hyllynä. Asentaa se, se on vastaava.

Molemmissa tapauksissa, jotka tadostavat lankun tasapainoiset, on sama suuruus ja suunta, jotka vaikuttavat samoihin toimintalinjoihin, mutta niitä käytetään eri kohdissa.

Siirrettävyysperiaate ja hetket

Oletetaan, että pisteeseen A on kohdistettu Fows F, hetki, joka syntyy tästä voimasta pisteen ympärillä tai esitetty kuvassa, on:

MJOMPIKUMPI = r --Lla × F

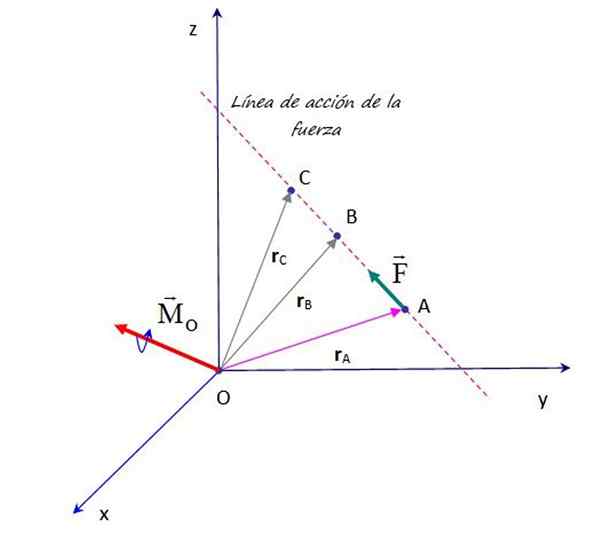Liuku- tai siirtovoima sen toimintalinjaa pitkin ei muokkaa sitä hetkeä, jota se käyttää pisteeseen tai. Lähde: f. Zapata.

No, siirrettävyysperiaate varmistaa sen F, Toiminnassa missä tahansa kohdassa sen toimintalinja, esimerkiksi pisteet B, C ja muut, on peräisin samasta hetkestä pisteeseen tai. Siksi on pätevä vahvistaa, että:

MJOMPIKUMPI = r --Lla × F  = r -B - × F = r -C × F

Ratkaisut

Harjoitus 1

Homogeenisella pallolla on massa m = 5 kg ja se lepää vaakasuoralla pinnalla ilman kitkaa.

    • a) Piirrä kaaviossa pallon pinnan aiheuttama voima.
    • b) Rakenna pallon vapaa kehon kaavio
    • c) Laske pallon pinnan käyttämän normaalin voiman arvo.

  • Ratkaisut A ja B

Kaaviossa a) pallon pinnan aiheuttama voima on esitetty, kutsutaan normaaliksi N, Koska se on kohtisuorassa pintaan. Voiman levityspiste osuu samanaikaisesti pallon tukipisteen kanssa pinnalla (vihreä piste) ja toimintalinja on pystysuora, joka kulkee pallon geometrisen keskuksen läpi.

Voi palvella sinua: Maan magnetosfääri: Ominaisuudet, rakenne, kaasut

Kaaviossa b) Pallon vapaa kehon kaavio, jossa normaalia lukuun ottamatta paino on esitetty, jota levitetään painopisteessä, merkitty keltaisella pisteellä.

Lähetettavuusperiaatteen ansiosta normaali voima N Se voidaan siirtää tähän pisteeseen muuttamatta sen vaikutuksia palloon. Nämä vaikutukset eivät ole muita, jotka pitävät palloa tuettuna pöydällä tasapainossa.

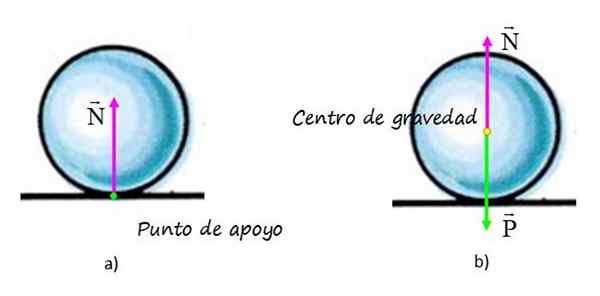Kuvassa a) vasemmalla, normaali vaikuttaa pallon tukipisteeseen pinnan kanssa. Kuvassa b), vapaassa rungon kaaviossa normaali siirretään painopisteeseen, koska pystysuora on sen toimintalinja. Sen vaikutuksia ei muuteta, koska se tasapainottaa painoa siten, että pallo on tasapainossa. Lähde: f. Zapata.

  • Liuos C

Koska pallo on tasapainossa, pitäen positiivisena merkityksenä pystysuoraan ja negatiiviseen pystysuoraan, Newtonin toinen laki johtaa:

N - p = 0

Eli paino ja normaali ovat tasapainossa, siksi ne ovat samat suuruudessa:

N = p = mg = 5 kg × 9.8 m/s2 = 49 n, suunnattu pystysuunnassa.

Harjoitus 2

Ilmoita, täyttyykö seuraavissa tapauksissa siirrettävyysperiaate:

  • Ensimmäinen tapaus

Jäykälle runkoon asetettu 20 N: n vaakasuora voima korvataan toisella 15 N: n voimalla, jota käytetään kehon toiseen pisteeseen, vaikka molemmat levitetään samaan suuntaan.

    • Ratkaisu

Tässä tapauksessa siirrettävyysperiaatetta ei toteuteta, koska vaikka kaksi voimaa sovelletaan samaan suuntaan, toisella voimalla ei ole samaa suuruutta kuin ensimmäisellä. Siksi yhtä siirrettävyysperiaatteen välttämättömistä olosuhteista ei anneta.

  • Toinen tapaus

Jäykälle runkoon levitetty 20 n vaakasuora voima korvataan toisella 20 N: stä, jota levitetään kehon toiseen pisteeseen ja pystysuunnassa.

    • Ratkaisu
Voi palvella sinua: Planck Constant: kaavat, arvot ja harjoitukset

Tässä yhteydessä siirrettävyysperiaatetta ei täyttyä, koska vaikka kahdella voimalla on sama moduuli, ne eivät koske samaan suuntaan. Jälleen yhtä siirrettävyyden periaatteen välttämättömistä olosuhteista ei anneta. Voidaan sanoa, että nämä kaksi voimaa ovat vastaavia.

  • Kolmas tapaus

10 n voima muutetaan vaakasuoraan jäykään runkoon, jota myös sovelletaan myös kehon toiseen pisteeseen, mutta samaan suuntaan ja merkitykseen.

    • Ratkaisu

Tässä tapauksessa siirrettävyysperiaate täyttyy, koska nämä kaksi voimaa ovat saman suuruudessa ja niitä käytetään samaan suuntaan ja merkitykseen. Kaikki lähetettävyysperiaatteen tarvittavat olosuhteet täyttyvät. Voidaan sanoa, että nämä kaksi voimaa ovat vastaavia.

  • Neljäs tapaus

Voima on liukuu toimintalinjan suuntaan.

    • Ratkaisu

Tässä tapauksessa siirrettävyysperiaate täyttyy, koska samalla voimalla käytetyn voiman suuruus ei vaihtele ja se liukuu toimintaviivaansa. Jälleen kaikki tarpeelliset siirrettävyysperiaatteen olosuhteet täyttyvät.

Harjoitus 3

Jäykällä rungossa on kaksi ulkoista voimaa. Nämä kaksi voimaa kohdistuvat samaan suuntaan ja samaan suuntaan. Jos ensimmäinen moduuli on 15 N ja toisen 25 N: n, minkä ehtojen tulisi kolmannen ulkoisen voiman, joka korvaa kahden edellisen tuloksena vastaavan lähettämisperiaatteen täyttämiseksi?

  • Ratkaisu

Toisaalta tuloksena olevan voiman arvon on oltava 40 N, mikä on seurausta kahden voiman moduulin lisäämisestä.

Toisaalta tuloksena olevan voiman on toimittava missä tahansa suorassa linjassa, joka liittyy kahden voiman kaksi kohdasta.

Viitteet

  1. Bedford, 2000. -Lla. Tekniikan mekaniikka: staattinen. Addison Wesley. 
  2. Olut, f. 2010. Insinöörien vektorimekaniikka. McGraw Hill. Viides. Painos.
  3. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. Kuudes. Ed Prentice Hall.
  4. Hibbeler, R. 2004. Tekniikan mekaniikka: Statiikka. Prentice Hall.
  5. Meriam, J.Lens. 2012. Tekniikan mekaniikka: Statiikka. 7. painos. Wiley & Sons.