Kuusikulmainen prisma

Selitämme, mikä kuusikulmainen prisma on, sen ominaisuudet, elementit, alue, kärkipisteet, reunat ja niiden laskeminen.

Mikä on kuusikulmainen prisma?

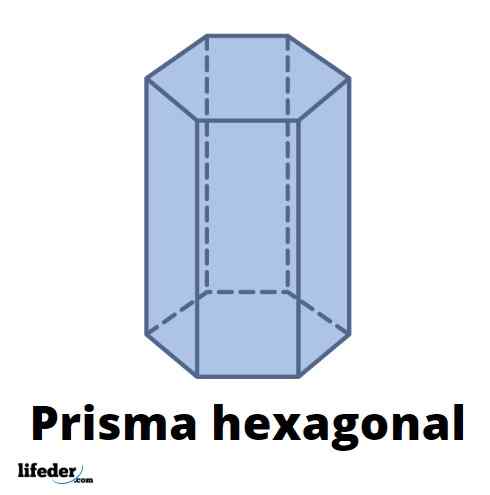
Eräs Kuusikulmainen prisma Se on kolmiulotteinen runko, joka koostuu kahdesta kuusikulmiosta ja sivusta, jotka on muotoiltu suorakulmioksi tai rinnakkaisohjelmaksi. Sitä löytyy luonnosta, esimerkiksi mineraalien, kuten berylliumin, grafiitin, sinkin ja litiumin, kiteisestä rakenteesta.

Kuusikulmaisen prisman elementit ovat pohja, kasvot, reuna, korkeus, kärki, radio ja apoteemi. Niistä voit laskea alueet ja volyymit.

Ylähahmo näyttää kuusikulmaisen prisman suorakaiteen muotoisilla sivuilla; tarkoittaen, Suora kuusikulmainen prisma. Pohjojen kuusikulmiot ovat säännöllisiä, ts. Heidän sisäiset puolensa ja kulmansa ovat samat. Kuusikulmaiset prisman kasvot voivat kuitenkin olla epäsäännöllisiä kuusikulmaisia.

Kuusikulmaisen prisman ominaisuudet

1- kuusikulmainen prisma on kolmiulotteinen hahmo, jossa on kuusikulmainen emäs.

2- On olemassa laaja valikoima esineitä, jotka reagoivat tähän määritelmään, ja silti ne ovat melko erilaisia.

Seuraavassa kuvassa on erilaisia ​​kuusikulmaisia ​​prismoja: vasemmalla säännöllisten kasvojen suoran kuusikulmaisen prisman, oikealla ja alas kaksi epäsäännöllisiä kasvoja. Alla olevan prisman pohjassa olevalla kuusikulmiolla on erityisyys: se on kovera, Mikä tarkoittaa, että jotkut sen sisäkulmista ovat suurempia kuin 180 °.

Erilaisia ​​kuusikulmaisia ​​prismejä. Lähde: Wikimedia Commons.

Toisaalta yllä olevien prismien kuusikulmaiset emäkset ovat monikulmioita kupera: Kaikkien sisäisten kulmien mittaan alle 180 °.

Kuusikulmaiset prismaelementit

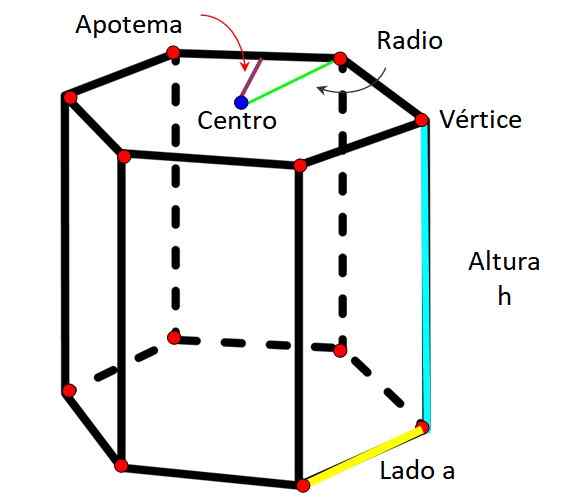Kuusikulmaiset prismaelementit. Lähde: f. Zapata

Kuten jokainen prisma, myös kuusikulmaiselle prismalle on ominaista seuraavat elementit:

Voi palvella sinua: moninkertainen käänteinen: Selitys, esimerkit, ratkaisut harjoitukset

-Pohjat: Kahden (2) lukumäärän kuusikulmion ja yhtenäisen muodossa, toisin sanoen. Kuusikulmainen kasvot voivat olla säännöllisiä tai epäsäännöllisiä.

-Kasvot: Kuusikulmaisella prismalla on yhteensä kahdeksan (8) kasvot, jotka voidaan laskea käyttämällä kuvaa 1. 8 kasvoista kaksi (2) ovat emäksiä ja kuusi (6) ovat sivuttaisia.

-Reuna: Segmentti liittyy prisman kahteen emäkseen tai kahteen puoleen.

-Korkeus: Se on etäisyys prisman kahden pinnan välillä. Samaan aikaan reunan pituuden kanssa suoran prisman tapauksessa.

-Kärki: yhteinen kohta pohjan ja kahden sivupuolen välillä.

Jos prisman emäkset ovat säännöllisiä, kuvan symmetria mahdollistaa tavallisen kuusikulmion lisäosien määrittelemisen -lla.

-Radio: Se on etäisyys, joka mitataan kuusikulmion keskustasta ja mitä tahansa kärkipistettä.

-Apoteemi: Segmentti menee kuusikulmaisen pinnan keskustasta toisen puolen keskelle.

Näiden elementtien avulla lasketaan alueet ja tilavuudet, kuten myöhemmin näemme.

Kaavat

Kuusikulmaiseen prismaan liittyy lukuisia kaavoja. Ne aikovat laskea sivupohjansa ja kasvojensa pinta -alan, sen tilavuuden ja muut tärkeät ominaisuudet. Tavallisen kuusikulmion, epäsäännöllisen kuusikulmion ja rinnakkaisogrammin sekä kehän alueet ovat hyödyllisiä.

Tasaisen kuvion kehä

Se on sen ääriviivat, jotka monikulmion, kuten kuusikulmion, tapauksessa on sen sivujen summa. Jos kuusikulmio on säännöllinen sivuttain -lla, Kehälle on kaava P-

P = 6.-lla

Säännöllinen kuusikulmioalue

Soitetaan ALS: lle ja L: lle_-Lla Apoteemin pituudella. Alueelle annetaan:

Voi palvella sinua: Ryhmätiedot: Esimerkit ja liikunta ratkaistu

A = p. Lens_-Lla/2 = 6a. Lens_-Lla/2

Missä P on kuvan kehä.

Sivun koosta riippuen -lla, Alue voidaan myös laskea:

A = 2.5981.-lla²

Epäsäännöllinen kuusikulmioalue

Ei ole erityistä kaavaa, koska se riippuu sivujen järjestelystä, mutta kuusikulmio voidaan jakaa kolmioihin, laskea kunkin pinta -ala ja lisätä ne.

Toinen menetelmä alueen löytämiseksi on Gauss -determinantit, joille on tarpeen tuntea kuusikulmioiden koordinaatit.

Rinnakkaisohjelma

A = pohja x korkeus

Joo -lla on pohja ja h Se on korkeus, alue on:

A = a.h

Kuusikulmainen prisma -alue

Se on emäksen alueiden summa -kaksi heksagonia -ja kasvot -6 suorakulmiot tai rinnakkaisohjelmat-.

Säännöllinen kuusikulmainen prisma -alue

Jos kuusikulmaisella prismalla on emäkset säännöllisten kuusikulmioiden muodossa ja sivuttaiset reunat ovat kohtisuorassa näihin tukikohtiin nähden, sen pinta -ala on summa:

A = 2 x 2.5981.-lla² + Kuudes.h

Missä -lla Se on kuusikulmion puoli ja h Se on prisman korkeus.

Epäsäännöllinen ja suora kuusikulmainen prisma -alue

Jos emäkset ovat epäsäännöllisiä kuusikulmioita, pinta -ala on laskettu:

A = 2a_pohja  + P.h

Missä:

--Lla_pohja Se on epäsäännöllinen kuusikulmainen pohjaalue.

-P on pohjan kehä.

-H on prisman korkeus

Kärjet

Jokaisessa kuusikulmaisessa kasvossa on 6 kulmaa tai kärkipistettä, mikä antaa yhteensä 12 huksikonaalisen prisman kärkeä.

Reunat

Prisman reunojen lukumäärän löytämiseksi on kaava. Suuri matemaatikko Leonhard Euler (1707-1783) löysi sen ja sitä kutsutaan Euler -lause polyhedrosille. Sanoo niin:

Voi palvella sinua: algebrallinen päättely

Jos c on kasvojen lukumäärä ja Vértices V: n ja kokonaisreunojen määrä. Onko totta että:

C+V = A+2

Kuusikulmaisen prisman määrät ovat: c = 8 ja v = 12. Siksi A on:

A = C + V - 2 = 8 + 12-2 = 18

Tilavuus

Minkä tahansa prisman, joka on suoran tai vino, säännöllisten tai epäsäännöllisten kasvojen, volyymi V on annettu:

V = pohjapinta -ala x korkeus

Siksi tarvitsemme kaavoja aiemmin näkemämme alueelle.

Esimerkiksi suoraa kuusikulmaista prismaa, jonka pohjat ovat säännöllisiä kuusikulmioita, tilavuus antaa:

V = 2.5981.-lla².h

Viitteet

1. Matematiikan avoin viite. Monikulmioalue. Toipunut: MathPenref.com.
2. Wikipedia. Prisma. Palautettu: on.Wikipedia.com.