Pentagonaalinen prisman ominaisuudet, osat, kärkipisteet, reunat, tilavuus

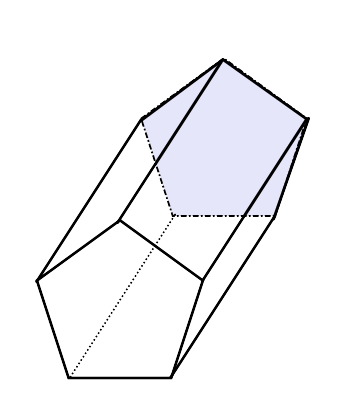
Eräs Pentagonaalinen prisma Se on kolmiulotteinen geometrinen luku, jonka emäksillä, identtisillä, on Pentagonin muoto, ja sen muodossa on yhteensä 5.

Jos kasvot ovat suorakaiteen muotoisia, sanotaan, että se on Suora viisikulmainen prisma, Vaikka reunat ovat taipuvaisia ​​tukikohtiin, niin se on vino pentagonaalinen prisma. Seuraavassa kuvassa on esimerkki jokaisesta.

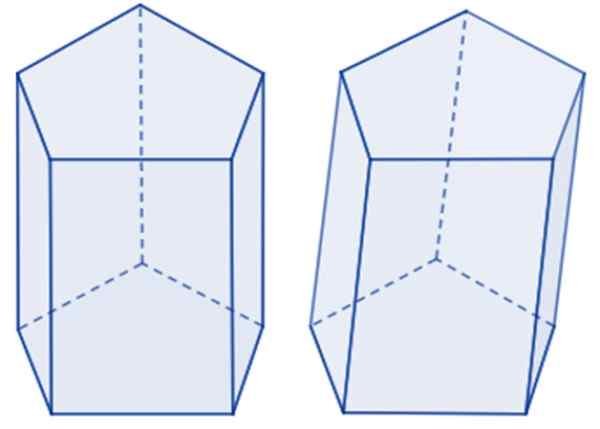Pentagonaalinen prisma vasemmalle ja vino oikealle. Lähde: Wikimedia Commons.

Pentagon -pohja voi olla säännöllinen, jos sen viidellä sivulla on sama mitta, samoin kuin sisäkulmat, muuten se on epäsäännöllinen pentagon. Jos prismapohja on säännöllinen, se on kyse Säännöllinen viisikulmainen prisma. Muuten on prisma epäsäännöllinen pentagonaali.

Modernissa rakenteessa käytettyjen pentagonaalisten prismien epäsäännöllinen pohjaprismat. Lähde: Taustakuvan leimahdus.

Pentagonaalinen prisma on harmoninen rakenne, jota käytetään esineiden arkkitehtuurissa ja suunnittelussa, kuten ylemmässä kuvassa esitetty moderni rakennus. Epäsäännölliset Pentagonin muotoiset ikkunat muodostavat prismien perustan.

[TOC]

Pentagonaalinen prisman ominaisuudet

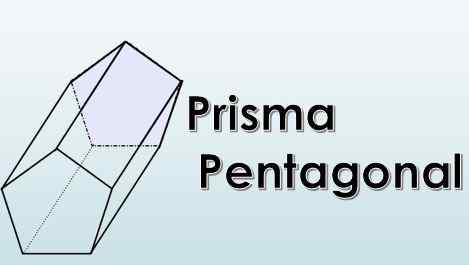
-Se on kolmiulotteinen geometrinen kuva, pinnat, jotka sitä muodostavat, sisältävät tietyn tilavuuden.

-Heidän emäksensä ovat viisikulmoja ja niiden sivupinnat voivat olla suorakulmioita tai rinnakkaisia.

-Siinä on kärkipisteitä -Prisma -ja reunojen kulmat -rannot tai rannat-.

-Jos perustat yhdistävät reunat ovat kohtisuorassa heihin, prisma on suora, ja jos ne ovat taipuvaisia, prisma on vino.

-Kun pohja on viisikulma, jonka sisäkulmat ovat alle 180º, prisma on kupera, Mutta jos yksi tai useampi sisäkulma on suurempi kuin 180º, se on prisma kovera.

Pentagonaalinen prismaelementit

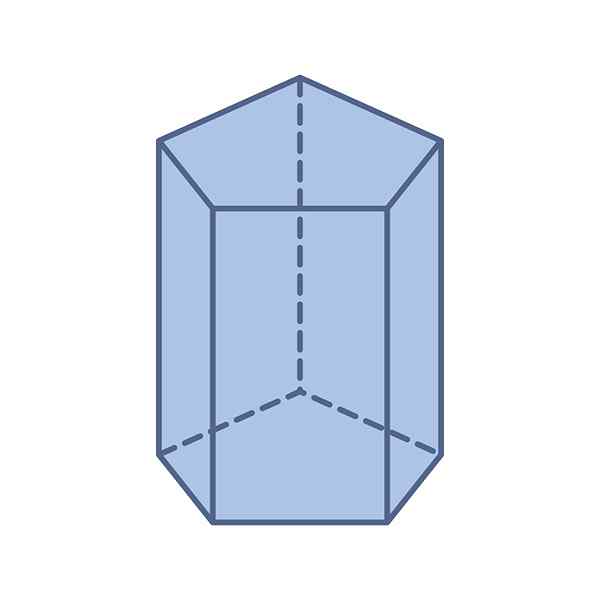
-Pohjat: Siinä on kaksi viisikulmaista ja yhtenäistä emäksistä -heidän mittauksensa ovat samat -joko säännölliset tai epäsäännölliset.

Voi palvella sinua: Yleinen kaava: neliömäiset yhtälöt, esimerkit, harjoitukset

-Kasvot: Pentagonaalisella prismalla on yhteensä 7 pintaa: kaksi viisikulmaista emäksiä ja viisi rinnakkaista ohjelmaa, jotka muodostavat sivut.

-Reuna: segmentti, joka liittyy kahteen emäkseen, esitetty punaisella kuvassa 3 tai se, joka liittyy kahteen puoleen.

-Korkeus: Etäisyys kasvojen välillä. Jos prisma on suora, tämä etäisyys on samanaikainen reunan koon kanssa.

-Kärki: yhteinen kohta pohjan ja kahden sivupuolen välillä.

Alemmassa kuvassa on tavallinen pentagonaalinen emäsprisma, jossa emäksen muodostavilla segmenteillä on yhtä suuri mitta, nimeltään -lla.

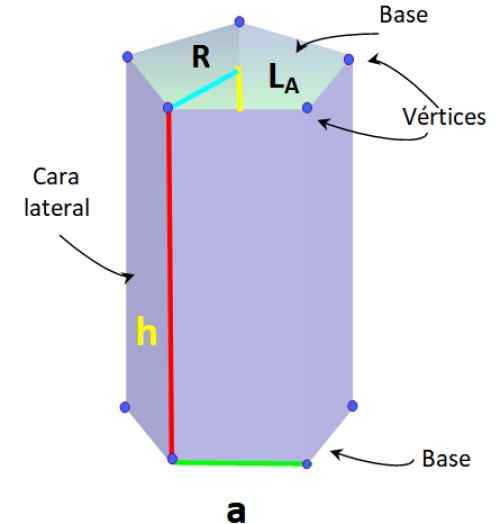 Säännölliset viisikulmaiset prismaelementit. Lähde: f. Zapata.

Tämän tyyppisellä prismalla on myös seuraavat elementit, jotka ovat tyypillisiä tavalliselle Pentagonille:

-Radio r: Etäisyys Pentagonin keskustan ja yhden kärjen välillä.

-Apoteemi l_-Lla: segmentti, joka liittyy keskustaan ​​Pentagonin yhden sivun keskipisteellä.

Kuinka monta kärkipistettä pentagonaalisella prismalla on?

Pentagonissa on 5 kärkeä ja koska pentagonaalisessa prismassa on kaksi pentagonia emäksinä, tällä ruumiilla on yhteensä 10 kärkeä.

Kuinka monta reunaa viisikulmaisella prismalla on?

Voit laskea geometristen kappaleiden reunojen lukumäärän, jolla on litteät kasvot, kuten prismat, käyttämällä Euler -lause Kuperille polyhedrosille. Leonhard Euler (1707-1783) on yksi suurimmista matemaatikoista ja fyysisiä historiassa.

Lause muodostaa suhteen kasvojen lukumäärän, jota kutsumme C: n, kärkipisteiden V ja kokonaisreunojen välillä seuraavasti:

C+V = A+2

Pentagonaalisen prisman kohdalla: c = 7 ja v = 10. Selvitys, reunojen lukumäärä:

Se voi palvella sinua: Bijjective Function: Mikä se on, miten se tehdään, esimerkkejä, harjoituksia

A = C+V-2

Arvojen korvaaminen:

A = 7 + 10 - 2 = 15

Pentagonaalisella prismalla on 15 reunaa.

Kuinka saada viisikulmaisen prisman tilavuus?

Pentagonaalisen prisman tilavuus mittaa sivujen ja emästen lukitseman tilan. Se on positiivinen määrä, joka lasketaan seuraavalla ominaisuudella:

Mikä tahansa taso, joka leikkaa prismaan kohtisuorassa reunoihinsa, luo risteyksen samalla tavalla kuin pohja, toisin sanoen samojen ulottuvuuksien pentagon.

Siksi viisikulmaisen prisman tilavuus on pohja -alueen ja prisman korkeus.

Olla -Lla_{B -} Pentagonaalinen pohjaalue ja h Prisman korkeus, sitten tilavuus V On:

V = a_{B -} X H

Tämä kaava on yleinen, ja se on voimassa mihin tahansa prismaan, joko tavallisessa tai epäsäännöllisessä, suorassa tai vinossa.

Prisman tilavuus tulee aina korkeaan yksiköinä kuutioon. Jos sivujen pituus ja prisman korkeus on annettu metreinä, tilavuus ilmaistaan ​​m³, että "kuutiomittarit" luetaan. Muita yksiköitä ovat cm³, km³, tuumaa³ ja enemmän.

- Säännöllinen viisikonaalinen prisman tilavuus

Pentagonal -prismissa säännölliset emäkset ovat säännöllisiä pentagoneja, mikä tarkoittaa, että sivu- ja sisäkulmat ovat samat. Kehon symmetrian vuoksi Pentagonin alue ja siksi tilavuus lasketaan helposti monin tavoin:

Sivun korkeuden ja mittauksen tunteminen

Olla -lla Pentagonaalisen pohjapuolen mitta. Tällöin pinta -ala on laskettu:

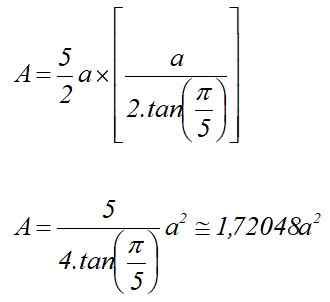
Siksi normaalin pentagonaalisen korkeuden H: n tilavuus on:

Voi palvella sinua: kuvitteelliset numerot: Ominaisuudet, sovellukset, esimerkit

V = 1.72048 a²⋅ H

Radion korkeuden ja mittauksen tunteminen

Kun Radio r Pentagonal -pohjasta tätä toista yhtälöä voidaan käyttää pohja -alueelle:

A = (5/2) r²⋅ Sen 72º

Tällä tavalla pentagonaalisen prisman tilavuus on antanut:

V = (5/2) r² ⋅ H ⋅ SEN 72º

Missä h Se on prisman korkeus

Apotem- ja kehän arvon pituuden,

Pentagonaalinen pohjapinta -ala voidaan laskea, jos sen kehä P tunnetaan, mikä on yksinkertaisesti sivujen summa, samoin kuin apoteemin mittaus_-Lla-

A = p. Lens_-Lla / 2

Kertomalla tämä lauseke korkeuden arvolla h, Meillä on prisman määrä:

V = P. Lens_-Lla .H / 2

- Epäsäännöllinen pentagonaalinen prisman tilavuus

Alussa annettu kaava on jopa pätevä, kun prisman perusta on epäsäännöllinen pentagon:

V = a_{B -} X H

Perusalueen laskemiseksi käytetään erilaisia ​​menetelmiä, esimerkiksi:

-Triangulaatiomenetelmä, joka koostuu Pentagonin jakamisesta kolmioihin ja kvadrilateriaaleihin, joiden vastaavat alueet lasketaan helposti. Pentagonin alue on näiden yksinkertaisempien lukujen alueiden summa.

-Gauss -determinantit -menetelmä, jolle sinun on tunnettava kuvan kärkipisteet.

Kun pinta -alan arvo on määritetty, se kerrotaan prisman korkeudella tilavuuden saamiseksi.

Viitteet

1. Alexander, D. 2013. Geometria. Viides. Painos. Cengage -oppiminen.
2. Matematiikan avoin viite. Monikulmioalue. Toipunut: MathPenref.com.
3. Maailmankaikkeuden kaavat. Euler -lause polyhedrosille. Toipunut: UniversOformulat.com.
4. Maailmankaikkeuden kaavat. Tavallisen Pentagonin alue. Toipunut: UniversOformulat.com.
5. Wikipedia. Prisma. Palautettu: on.Wikipedia.com.
6. Wikipedia. Pentagonaalinen prisma. Palautettu: on.Wikipedia.com.