Taajuuden todennäköisyyskonsepti, miten lasketaan ja esimerkkejä

Se Taajuuden todennäköisyys on Alaryhmä todennäköisyyden ja sen ilmiöiden tutkimuksessa. Sen tutkimusmenetelmä, joka koskee tapahtumia ja ominaisuuksia.

Esimerkiksi gummitan -kirjekuori sisältää 5 jokaisesta väristä: sininen, punainen, vihreä ja keltainen. Haluat määrittää todennäköisyyden, että jokaisen värin on poistuttava satunnaisen valinnan jälkeen.

Lähde: Pexels

On tylsiä kuvitella saada kumi, tallentaa se, palauttaa sen, ottaa kumi ja toistaa samat useita satoja tai useita tuhansia kertoja. Voit jopa tarkkailla käyttäytymistä useiden miljoonien iteraatioiden jälkeen.

Mutta päinvastoin on mielenkiintoista huomata, että muutaman toiston jälkeen odotettu 25%: n todennäköisyys ei ole täysin toteutunut, ainakaan ei kaikille väreille 100 iteraation jälkeen.

Taajuuden todennäköisyyslähestymistavassa arvojen allokointi tapahtuu vain monien iteraatioiden tutkimuksella. Tällä tavoin prosessi on suoritettava ja mieluiten rekisteröitävä tietokoneistetulla tai jäljiteltyllä tavalla.

Useat virrat hylkäävät taajuuden todennäköisyyden, väittäen empiirisyyden puute ja luotettavuus satunnaisissa kriteereissä.

[TOC]

Kuinka taajuustodennäköisyys lasketaan?

Kun ohjelmoi koe missä tahansa rajapinnassa, joka pystyy tarjoamaan puhtaasti satunnaisen iteraation, voit alkaa tutkia ilmiön taajuuden todennäköisyyttä arvotaulukon kautta.

Edellistä esimerkkiä arvostetaan taajuuslähestymistavasta:

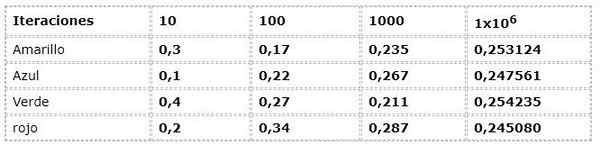
Numeeriset tiedot vastaavat lauseketta:

N (a) = iteraatioiden tapahtumien lukumäärä/ lukumäärä

Missä N (A) edustaa A -tapahtuman suhteellista taajuutta

”A” kuuluu mahdollisten tulosten tai näytetilaan ω

Se voi palvella sinua: Monilaitteet 8: mitä ovat ja selitys

Ω: punainen, vihreä, sininen, keltainen

Ensimmäisissä iteraatioissa on huomattava dispersio, kun taajuudet, joilla on jopa 30% eroista, havaitaan toistensa kanssa, mikä on erittäin korkea tosiasia kokeiluun, jolla teoreettisesti on tapahtumia, joilla on sama mahdollisuus (tasainen).

Mutta iteraatioiden kasvaessa arvot näyttävät yhä enemmän teoreettisen ja loogisen virran esittämille.

Suurten lukujen laki

Teoreettisen ja taajuuden lähestymistapojen välisenä odottamattomana sopimuksena syntyy suuren määrän laki. Jos todetaan, että huomattavan määrän iteraatioiden jälkeen taajuuskokeen arvot lähestyvät teoreettisia arvoja.

Esimerkissä voit huomata, kuinka arvot ovat arvioitu 0,250: een iteraatioiden kasvaessa. Tämä ilmiö on alkeellista monien todennäköisyysteosten päätelmissä.

Lähde: Pexels

Muut todennäköisyyslähestymistavat

On vielä 2 teoriaa tai lähestymistapaa todennäköisyyden käsitteeseen Taajuuden todennäköisyys.

Looginen teoria

Lähestymistaposi on suunnattu ilmiöiden deduktiiviseen logiikkaan. Edellisessä esimerkissä kunkin värin saamisen todennäköisyys on 25% suljettu. Toisin sanoen.

Subjektiivinen teoria

Se perustuu tietoihin ja aikaisempiin uskomuksiin, jotka jokaisella henkilöllä on ilmiöistä ja ominaisuuksista. Lausunnot kuten "Sataa aina pyhällä viikolla " He noudattavat samanlaisia ​​tapahtumia, joita on aiemmin tapahtunut.

Historia

Sen toteuttamispäivämäärän alku 1800 -luvulta, jolloin olen lainannut sitä useissa työssään Cambridge Englandissa. Mutta vasta 2000 -luvulla 2 tilastollista matematiikkaa kehitti ja muotoili Taajuuden todennäköisyys.

Voi palvella sinua: polynomiyhtälöt

Yksi heistä oli Hans Reichenbach, joka kehittää teoksiaan julkaisuissa, kuten "Todennäköisyysteoria", julkaistu vuonna 1949.

Toinen oli Richard von Mises, joka kehitti työnsä perusteellisemmin useiden julkaisujen kautta ja ehdotti todennäköisyyden pitämistä matemaattisena tieteenä. Tämä käsite oli uusi matematiikassa ja se merkitsisi kasvukauden alkua Taajuuden todennäköisyys.

Itse asiassa tämä tapahtuma tekee ainoan eron Vennin, Countin ja Helmin sukupolven tekemistä panoksista. Missä todennäköisyydestä tulee vastine, kuten geometria ja mekaniikka.

< La teoría de las probabilidades trata con Massiiviset ilmiöt ja toistuvat tapahtumat. Ongelmia, joissa joko sama tapahtuma toistetaan uudestaan ​​ja uudestaan, tai suuri joukko yhtenäisiä elementtejä on mukana samanaikaisesti> Richard von Mises

Massiiviset ilmiöt ja toistuvat tapahtumat

Kolme tyyppiä voidaan luokitella:

• Fysiikka: Luonnon obdoosikuviot satunnaisen tilan ulkopuolella. Esimerkiksi näytteen elementin molekyylien käyttäytyminen.
• Mahdollisuus:.
• Biologiset tilastot: Testikohteen valinnat niiden ominaisuuksien ja ominaisuuksien mukaisesti.

Teoriassa mittaavalla henkilöllä on rooli todennäköisyystiedoissa, koska hänen tietonsa ja kokemuksensa ilmaisevat tämän arvon tai ennusteen.

Siinä Taajuuden todennäköisyys Tapahtumia pidetään hoidettavina kokoelmina, joissa henkilöllä ei ole mitään roolia arviossa.

Ominaisuudet

Jokaisessa elementissä ilmenee ominaisuus, joka muuttuu tämän luonteen mukaan. Esimerkiksi fysikaalisen ilmiön tyypissä vesimolekyyleillä on erilaiset nopeudet.

Se voi palvella sinua: kolmiomaiset samankaltaisuuskriteerit

Pienen käynnistyksen yhteydessä tunnemme näytetilan ω, joka edustaa kokeen ominaisuuksia.

Ω: 1, 2, 3, 4, 5, 6

On muitakin määritteitä, kuten ω_P  tai olla pariton ω_Yllyttää

Ω_p : 2, 4, 6

Ω_Yllyttää : 1, 3, 5

Jotka voidaan määritellä ei -elementisiksi ominaisuuksiksi.

Esimerkki

• Haluat laskea kunkin mahdollisen summan taajuuden kahden noppan käynnistyksen yhteydessä.

Tätä varten ohjelmoidaan koe, jossa jokaisessa iteraatiossa lisätään kaksi satunnaista arvoa [1, 6].

Tiedot tallennetaan taulukossa ja suuren määrän suuntauksia tutkitaan.

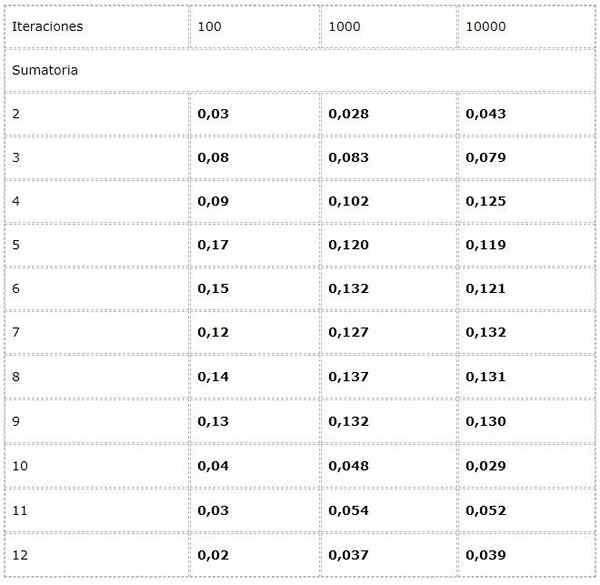
Havaitaan, että tulokset voivat vaihdella merkittävästi iteraatioiden välillä. Suurten määrien laki näkyy kuitenkin kahdessa viimeisessä sarakkeessa esitetyssä ilmeisessä lähentymisessä.

Viitteet

1. Tilastot ja todisteiden arviointi oikeuslääketieteellisille tutkijoille. Toinen painos. Colin G.G. Aitken. Matematiikan korkeakoulu. Edinburghin yliopisto, Iso -Britannia
2. Tietotekniikan matematiikka. Eric Lehman. Google Inc.
   F Thomson Leightonin matematiikan laitos ja tietotekniikka ja AI -laboratorio, Massachussetts Institute of Technology; Akamai Technologies
3. Aritmeettinen opettaja, osa 29. Matematiikan opettajien kansallinen neuvosto, 1981. Michiganin yliopisto.
4. Oppiminen ja opetusnumeroteoria: Tutkimus kognitiossa ja opetuksessa / toimittanut Stephen R. Campbell ja Rina Zazkis. Ablex Publishing 88 Post Road West, Westport CT 06881
5. Bernoulli, J. (1987). Ars injektointi- 4ème partitie. Rouen: Irem.