Adiabaattiset prosessityypit, esimerkit, harjoitukset ratkaistu

Eräs Adiabaattinen prosessi Se on se, jossa järjestelmän ja sen ympäristön välillä ei ole lämmönvaihtoa joko siksi, että se tapahtuu eristävässä väliaineessa, tai koska se kulkee hyvin nopeasti. Tämä tarkoittaa, että järjestelmän ympäristössä tämä on tutkittavan maailmankaikkeuden osa, lämpötilan muutoksia ei pidä kokea, vaan vain työskennellä.

Tämä on yksi termodynamiikan alkuaineprosesseista. Toisin kuin muut prosessit (isocoric, isobarinen ja isoterminen), mikään sen fyysisistä muuttujista ei pysy vakiona; toisin sanoen paineen, tilavuuden, lämpötilan ja entropian muutoksen suuruudet adiabaattisen prosessin kehittyessä.

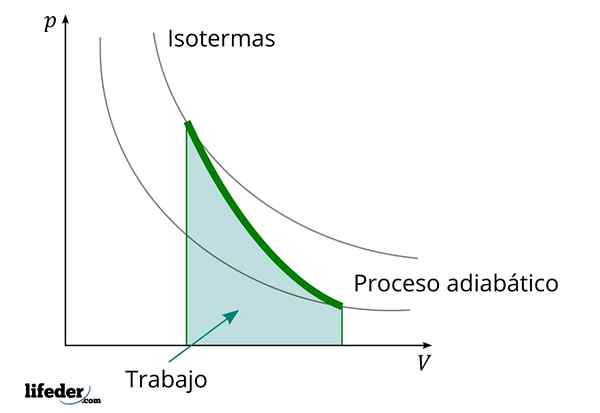
Adiabaattisen prosessin aikana, jossa tilavuus kasvaa, työn sisäinen energia vähenee

Toinen tärkeä ominaisuus adiabaattisille prosesseille on, että ne suorittavat tai kuluttavat työtä suhteessa järjestelmänsä sisäisen energian variaatioon; Tässä tapauksessa sen molekyyleistä kaasufaasissa. Tämä voidaan osoittaa ensimmäisen termodynamiikan lain ansiosta.

Tämän tyyppinen prosessi kattaa jokapäiväisessä elämässä ennen kaikkea geofysikaalisiin ilmiöihin ja jossain määrin mäntien toiminta dieselmoottoreissa. Lämmönsiirto estetään usein eristävää väliaineen avulla, mutta näiden prosessien nopeus sallii niiden todellisen kehityksen.

[TOC]

Palautuvat ja peruuttamattomat adiabaattiset prosessit

Palautuva

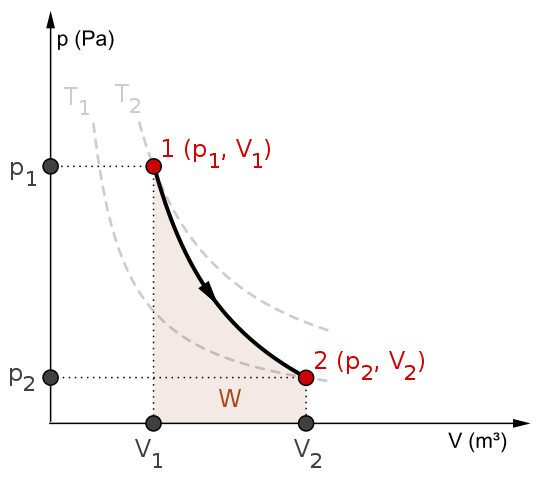P-V-kaavio ja työ W adiabaattiseen prosessiin. Lähde: Mikerun/CC BY-SA (https: // creativecommons.Org/lisenssit/by-SA/4.0)

Adiabaattiset prosessit voivat olla palautuvia tai peruuttamattomia. Ensimmäiset ovat kuitenkin vain teoreettisia välineinä jälkimmäisen tutkimiseksi. Siten palautuvat adiabaattiset prosessit sisältävät ihanteelliset kaasut, ja niistä puuttuu kitka ja muut mahdollisuudet, jotka aiheuttavat lämmönsiirtoa järjestelmän ja sen ympäristön välillä.

Harkitse esimerkiksi P-V-kaaviota palautuvaa adiabaattista prosessia ylhäältä. T₁ ja T₂ vastaa kahta isotermia, joihin paineet P ja volyymit V järjestelmä vaihtelee.

Valtioiden keskuudessa (P₁, V₁) Ja p₂, V₂) Suoritetaan palautuva adiabaattinen laajennus, koska siirrymme Volume V: stä₁ yhdelle v₂, isompi, nuolen suunnan jälkeen.

Näin toimiessa järjestelmä jäähtyy, mutta noudattamatta isotermien käyttäytymistä. Käyrän alla oleva alue vastaa työtä W, jonka arvo on positiivinen, koska se on laajennus.

Tässä prosessissa entropia pysyy vakiona, ja siksi sanotaan, että se on isontrooppinen. Tämän palautuvuuden matemaattinen käsittely tuottaa joukon yhtälöitä, joiden kanssa on mahdollista arvioida muita järjestelmiä.

Voi palvella sinua: elektrolyyttiset solut

Peruuttamaton

Peruuttamattomat adiabaattiset prosessit, toisin kuin palautuvat, eivät ole graafisia P-V-kaavioissa, joilla. Nämä prosessit sisältävät todellisia kaasuja, joten ihanteellisten kaasujen yhtälö ja niiden johdannaiset eivät ole suoraan sovellettavissa niihin.

Ne kulkevat nopeasti, estäen lämmönsiirron järjestelmän ja sen ympäristön välillä. Lisäksi niissä entropia kasvaa, kuten termodynamiikan toisessa laissa todetaan.

Esimerkkejä adiabaattisista prosesseista

Eristämiskyky, kuten termosten esittämät, on yksi keskeisistä tekijöistä prosessin kehittymiselle

Joitakin esimerkkejä adiabaattisista prosesseista mainitaan alla.

Laajennus ja ymmärrys

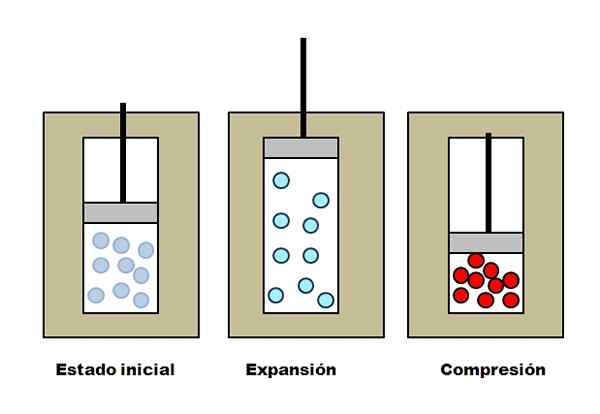Adiabaattinen laajennus ja ymmärrys. Lähde: Gabriel Bolívar.

Oletetaan, että kolme eristävää liiviä, jotka sisältävät osastoja täynnä kaasua. Alkuvaiheessa mäntä ei ole painetta kaasua. Sitten männän annetaan nousta, mikä lisää tilavuutta, jonka läpi kaasumolekyylit voivat liikkua, aiheuttaen sen sisäisen energian vähentymisen; Ja siksi lämpötilan lasku.

Päinvastoin tapahtuu adiabaattisen kompression kanssa: mäntä suorittaa kaasun työtä vähentäen sen tilavuutta, jonka sen molekyylit voivat käyttää. Sisäinen energia kasvaa tällä kertaa, mikä merkitsee myös lämpötilan nousua, jonka lämpö ei voi hajonnut ympäristöä kohti eristysliivin takia.

Magman nousu

Kanavat, joissa magma nousee tulivuoren sisällä.

Äänen leviäminen

Kaasut ovat häiriintyneet ja laajennetaan ääniaallon mukaan jäähdyttämättä tai kuumaa niitä ympäröivää ilmaa.

Foehn -vaikutus

Foehn -vaikutus on esimerkki adiabaattisista prosesseista geofysiikan alalla. Ilmamassat nousevat kohti vuoren yläosaa, jossa he kokevat vähemmän painetta, joten heidän molekyylinsä laajenevat ja viileät, mikä johtaa pilven muodostumiseen.

Ne kuitenkin tuskin laskeutuvat vuoren toiselle puolelle, paine kasvaa ja siksi molekyylit puristetaan ja nostavat niiden lämpötilaa aiheuttaen pilven katoamisen.

Voi palvella sinua: kloorobentseeni (C6H5CL)

Seuraavassa videossa tätä ilmiötä voidaan arvostaa:

Ratkaisut

Lopuksi pari harjoitusta ratkaistaan. On tärkeää, että seuraavat yhtälöt ovat käsillä:

ΔU = Q - W (termodynamiikan ensimmäinen laki)

Mutta ilman lämmönsiirtoa, Q = 0 y:

ΔU = - W (1)

Tämä on: Jos työ W on positiivinen, ΔU on negatiivinen ja päinvastoin. Toisaalta meillä on myös:

W = -nC_VΔt (2)

Se, kun olet soveltanut ihanteellista kaasun yhtälöä (pv = nRt), ja T: n korvaaminen ja ratkaiseminen₂ ja T₁ meillä tulee olemaan:

W = (c_V/R) (P₁V₁ - P₂V₂) (3)

On R: n arvo yhtä suuri kuin 0.082 l · atm/mol · k tai 8.314 j/mol · k

Adiabaattisissa prosesseissa on tärkeää tietää C -suhde_P/C_V tunnetaan nimellä γ:

γ = c_P/C_V    (4)

Joka mahdollistaa T-V- ja P-V-suhteiden luomisen:

T₁V₁^γ-1 = T₂V₂^γ-1   (5)

P₁V₁^γ = P₂V₂^γ    (6)

Ja myös C: n likimääräiset lämmitteet_P ja c_V Ne vaihtelevat riippuen siitä, ovatko kaasut monoatomia, diatomia jne.

Harjoitus 1

Kaasu suorittaa 600 J: n työtä eristetyn osaston kautta. Mikä on sen sisäisen energian muutos? Lämpötilojen väheneminen tai kasvaja? Ja ottaen huomioon, että se on monoatominen kaasu, laske myös y y.

Tiedot:

W = +600J

ΔU = ¿?

γ =?

W -työ on positiivista, koska kaasu toimii ympäristössä. Eristetyn osaston sisällä q = 0, ja siksi meillä on yhtälö (1):

ΔU = - W

Eli ΔU on yhtä suuri kuin:

ΔU = - (+600J)

= -600J

Mikä tarkoittaa, että kaasun sisäinen energia laski 600 J. Jos ΔU laskee, samoin lämpötila, niin kaasu jäähtyy työn tekemisen seurauksena.

Koska tämä kaasu on monoatominen,

C_V = 3/2 r

C_P = 5/2 r

Ja oleminen

γ = c_P/C_V

= (5/2 R)/(3/2 R)

= 5/3 tai 1.66

Harjoitus 2

Kontissa 7 moolia O₂ Ne puristettiin 15 litran ja 9 litran tilavuudesta. Tietäen, että alkulämpötila oli 300 K, laske: Kaasulle tehty työ.

Tiedot:

n = 7 moolia tai₂

T₁ = 300 K

V₁ = 15 l

V₂ = 9 l

W = ¿?

Se on peruuttamaton adiabaattinen ymmärrys. Meillä on kaksi yhtälöä ratkaistaksesi W:

W = -nC_VΔt (2)

W = (c_V/R) (P₁V₁ - P₂V₂) (3)

Paineet voivat laskea ne, mutta aikaa säästääksesi on parempi jatkaa yhtälöiden kanssa:

Voi palvella sinua: tislattua vettä

W = -nC_VΔt

= -nC_V (T₂-T₁-A

Tarvitsemme c_V ja T₂ W: n määrittämiseksi. Happea, joka on diatominen kaasu, on c_V yhtä suuri kuin 5/2 r:

C_V (JOMPIKUMPI₂) = 5/2 r

= 5/2 (8.314 J/mol · K)

= 20.785 j/mol · k

Meidän on laskettava t₂. Siirrymme yhtälöön (5):

T₁V₁^γ-1 = T₂V₂^γ-1

Mutta ennen sen käyttämistä sinun on määritettävä ensimmäinen c_P ja γ:

C_P (JOMPIKUMPI₂) = 7/2 r

= 7/2 (8.314 J/mol · K)

= 29.099 J/mol · K

Γ yhtä suuri kuin:

γ = c_P/C_V

= (29.099 J / mol · K) / 20.785 j/mol · k

= 1.4

Joten voimme puhdistaa tämän₂ Yhtälöstä (5):

T₁V₁^γ-1 = T₂V₂^γ-1

T₂ = (T₁V₁^γ-1) / (V₂^γ-1-A

= [(300k) (15L)^1.4-1] / (9L)^1.4-1

= 368.01 K

Ja lopuksi ratkaisemme W:

W = -nC_VΔt

= -(7 mol O₂) (kaksikymmentä.785 J/mol · K) (368.01 K - 300 K)

= -9895.11 J O -9.895 kJ

Harjoitus 3

Neonsäiliö laajenee adiabaattisesti ja aluksi huoneenlämpötilassa (t = 298k) 12 litrasta 14 litraan. Tietäen, että sen alkuperäinen paine oli 3 atm, mikä on kaasun tekemä työ?

Tiedot:

T₁ = 298 K

V₁ = 12 L

V₂ = 14 L

P₁ = 3 atm

W = ¿?

Yhtälö (3) antaa meille mahdollisuuden määrittää W paineiden arvoilla:

W = (c_V/R) (P₁V₁ - P₂V₂-A

Mutta meiltä puuttuu c_V Ja p₂.

Lopullinen paine voidaan laskea yhtälöllä (6):

P₁V₁^γ = P₂V₂^γ

On γ yhtä suuri kuin C_P/C_V. Koska neon on monoatominen kaasu, meillä on sen C -arvot_P ja c_V Ne ovat vastaavasti 5/2R ja 3/2R. Laskemme sitten γ:

γ = c_P/C_V

= (5/2R)/(3/2R)

= 5/3 tai 1.66

Tyhjentämme p₂ Yhtälöstä (6):

P₂ = (P₁V₁^γ) / V₂^γ

= [(3 atm) (12 l)^5/3] / (14 l)^5/3

= 1.40 atm

Ja työ on yhtä suuri kuin:

W = (c_V/R) (P₁V₁ - P₂V₂-A

= (3/2) [(3 atm) (12 l) - (1.40 atm) (14 l)] (101300 PA/1 atm) (0.001 m³/L) (KJ/1000 J)

= 2.49 kJ

Muutostekijöitä käytetään L · ATM A PA · M: n muuntamiseen³, joka vastaa 1 J. Neonkaasu laajenee, joten sen paine laskee ja tehdessään ympäristössä tämä on positiivinen. Lisäksi sen sisäinen energia ΔU laskee, samoin kuin sen lämpötila, jäähdytys laajennusprosessissa.

Viitteet

1. Walter J. Moore. (1963). Fysikaalinen kemia. Kemiallisessa kinetiikassa. Neljäs painos, Longmans.
2. Iranin. Levine. (2009). Fysikaalis -periaatteet. Kuudes painos. MC Graw Hill.
3. Wikipedia. (2020). Adiabaattinen prosessi. Haettu: vuonna.Wikipedia.org
4. Jones, Andrew Zimmerman. (18. elokuuta 2020). Themodynamiikka: Adiabaattinen prosessi. Toipunut: Admingco.com
5. Devoe Howard & Neils Tom. (9. elokuuta 2020). Adiabaattiset muutokset. Kemian librettexts. Palautettu: Chem.Librettexts.org