Ristituote

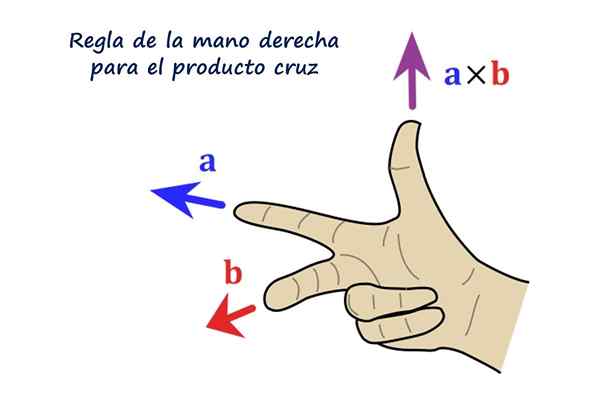
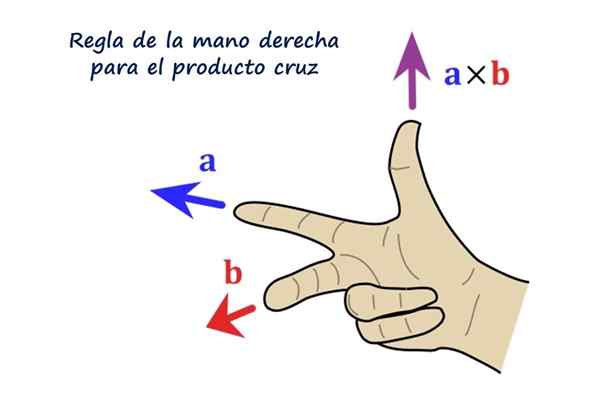Oikea sääntö vektorituotteelle. Lähde: f. Zapata.

Mikä on ristituote tai vektorituote?

Hän Ristituote, Kutsutaan myös vektorituote, se on eräänlainen tuote, joka suoritetaan kahden vektorin välillä ja tulokset toiseen vektoriin, kohtisuorassa kahden ensimmäisen määrittelemän tason suhteen.

Ristituote minkä tahansa kahden vektorin välillä -lla ja b -, Se johtaa toiseen vektoriin R -, Matemaattisesti kirjoitetaan seuraavasti:

-lla × b - = R -

Se lukee näin: “Cruz B yhtä suuri kuin r ".

Painetussa tekstissä vektorit on kirjoitettu rohkeilla sanoituksilla tai nuolella kirjaimella, jotta ne voidaan erottaa niiden suuruudesta tai moduulista. Tätä varten niitä käytetään, vuorottelevasti, moduulipalkit ja nykyiset kirjaimet, joten vektorin absoluuttinen arvo -lla Symboli on kirjoitettu näin:

│-lla│ = a

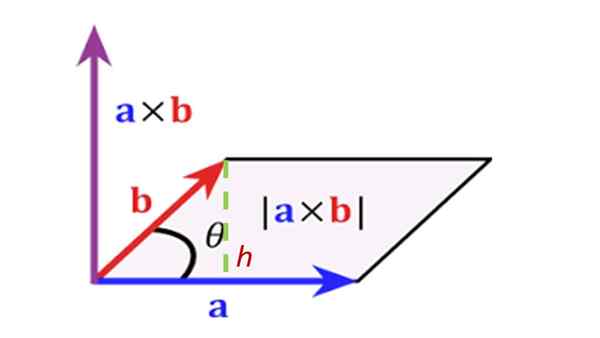
Vektorituotteen absoluuttinen arvo tai moduuli kahden vektorin välillä lasketaan kertomalla molempien vektorien moduuli kulman θ läpi:

R = a ∙ b ∙ sen θ

Vektorin suunta R - Se on kohtisuorassa vektorien vertaansa -lla ja b -. Käsitys R - Se on dekstrogyr -lla kohti b - Ja käytännössä se määritetään oikean käden sääntöjen avulla, joka koostuu oikean käden indeksin, keskipitkän ja peukalon sijoittamisesta seuraavasti:

• Etusormi sijoitetaan vektorin jälkeen -lla
• Keskisormen kanssa seuraa vektoria b -
• Peukalo, laajennettu, osoittaa vektorin suunnan ja suunnan R -.

Tätä järjestystä on noudatettava tarkalleen, koska vektorituote ei ole kommutatiivinen, eli -lla × b - ≠ b - × -lla Ja jos vektorit vaihdetaan, oikeaa tulosta ei saatu.

Voi palvella sinua: olemassaolo ja ainutlaatuisuus lause: esittely, esimerkit ja harjoitukset

Lukijaa kehotetaan sijoittamaan oikea käsi, kuten kuva osoittaa, vasemmalle osoittava indeksi edustaa vektoria -lla, Keskisormi seuraa b - Ja se osoittaa suoraan lukijalle, lopulta peukalo osoittaa osoittaen vektorin suunnan ja suuntaan -lla × b - = R -.

Cruz -tuotteiden ominaisuudet

-Kahden vektorin välinen risti- tai vektorituote johtaa aina toiseen vektoriin.

-Ristituote ei siis ole kommutatiivinen: siksi: -lla × b - ≠ b - × -lla.

-Ristituotteelle on totta, että: -lla × b - = - (b - × -lla-A. Tätä ominaisuutta kutsutaan anti-conminacy.

-Saatu vektorituotteen vektori kahden vektorin välillä on kohtisuorassa (normaali) mainituille vektoreille.

-Edellä mainitusta seuraa, että vektorien välinen vektorituote on NULL. Erityisesti -lla × A = 0.

-Ristituote noudattaa jakelulaki summan suhteen: -lla × (b -+c) = -lla × b - + -lla × c

-Jos m on skalaari, niin m (-lla × b -) = m -lla × b - = -lla × M b -

Ristituote yksikkövektoreiden välillä

Kolme yksikkövektoria, nimeltään Yllyttää, J - ja k -k -, Ne ovat kohtisuorassa toisiinsa nähden ja osoittavat tilaa koskevat kolme merkittävää suuntaa: korkea, leveä ja syvyys. Nämä osoitteet ovat kohtisuorassa toisiinsa nähden.

Yksikön vektorien välinen vektorituote määritetään helposti oikeanpuoleisen säännön kautta ja pitäen mielessä ristin tuotteen ominaisuudet:

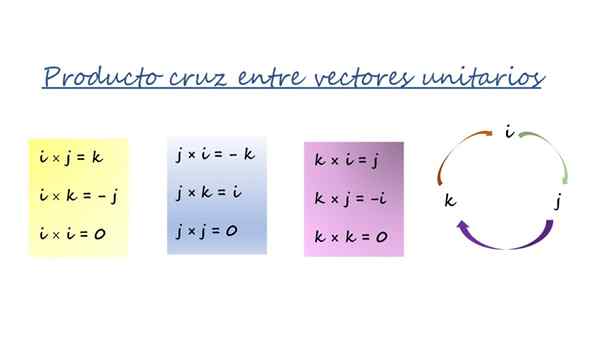Cartesian yksikkövektorien vektorituote. Lähde: f. Zapata.

Kuvan kolme värillistä laatikkoa on tiivistetty kierroksella nuolilla oikealla ja sitä käytetään tällä tavalla:

-Kun kerrotaan nuolen suuntaan, tulos on nuolen edessä oleva vektori ja sillä on positiivinen merkki. Esimerkiksi kertomalla vektorisesti J - ja k -k -, Kolmas vektori on Yllyttää, Ja kun järjestys seuraa nuolen merkitystä, merkki on +.

Voi palvella sinua: vektoritoiminnot

-Ja jos se moninkertaistuu vastakkaiseen suuntaan kuin nuoli, tulos on kolmas vektori nuolen edessä, mutta negatiivisella merkkillä.

Yksikkövektorit muodostavat tukikohdan, joten mikä tahansa muu vektori voidaan kirjoittaa niistä. Tämä helpottaa huomattavasti ristikkäisen tuotteen laskemista kahden mielivaltaisen vektorin välillä avaruudessa.

Kuinka analysoida kahden vektorin ristikkäin analyyttisesti

Kun vektorit -lla ja b - Heillä on mielivaltainen suunta avaruudessa, kun komponentteja on kutakin, on helpompaa laskea poikkituote analyyttisellä tavalla, ilmaista niitä yksikkövektorien suhteen Yllyttää, J - ja k -k --

• -lla = a_x Yllyttää + -lla_ja J - + -lla_{z -z} k -k -
• b - = b_x Yllyttää + b -_ja J - + b -_{z -z} k -k -

Nyt käytetään kertolaskuominaisuutta, joka pätee myös ristituotteeseen:

-lla × b - = (a_x Yllyttää + -lla_ja J - + -lla_{z -z} k -k -) × (b_x Yllyttää + b -_ja J - + b -_{z -z} k -k -) =

= (a_x Yllyttää × B_x Yllyttää) + (a_x Yllyttää × B_ja J -) + (a_x Yllyttää × B_{z -z} k -k -) + (a_JA J - × B_x Yllyttää) + (a_JA J - × B_ja J -) + (a_JA J - × B_{z -z} k -k -) + (a_{Z -z} k -k - × B_x Yllyttää) + (a_{Z -z} k -k - × B_ja J -) + (a_{Z -z} k -k - × B_{z -z} k -k --A

Ristituotteet yhtä suuret yksikkövektorien välillä peruutetaan, koska ne ovat rinnakkaisia ​​vektoreita, jotka vähentävät tämän lausekkeen 6 termille:

-lla × b - = (a_x Yllyttää × B_ja J -) + (a_x Yllyttää × B_{z -z} k -k -) + (a_JA J - × B_x Yllyttää) + (a_JA J - × B_{z -z} k -k -) + (a_{Z -z} k -k - × B_x Yllyttää) + (a_{Z -z} k -k - × B_ja J --A

Lopuksi, käyttämällä yllä olevaa kuvaa, kukin tuote johtaa:

-lla × b - = a_x b -_ja k -k - + -lla_x b -_{z -z} ( -J -) + a_JA b -_x ( -k -k -) + a_JA b -_{z -z} Yllyttää + -lla_{Z -z} b -_xJ - + -lla_{Z -z} b -_ja ( -Yllyttää) =

= (a_JA b -_{z -z} - a_{Z -z} b -_ja-A Yllyttää + (_{Z -z} b -_x - a_x b -_{z -z}-A J - + (_x b -_ja - a_JA b -_x-A k -k -

Cruz -tuote determinantin kautta

Yllä olevaa kaavaa ei tarvitse muistaa, mutta soveltaa edellisen hahmon kierrosta kätevästi tai yksinkertaisesti suorittaa alla esitetty determinantti, joka on täysin vastaava:

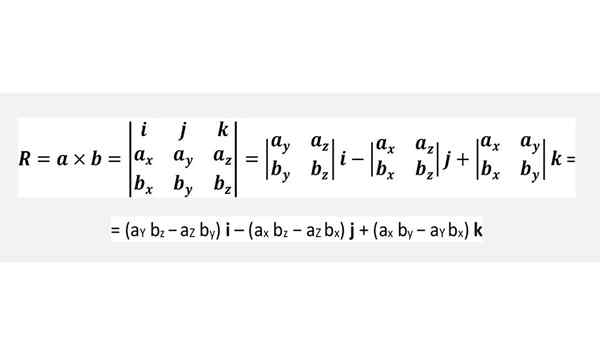
Esimerkki

Olettaen vektorit -lla ja b - ovat:

• -lla = 5 Yllyttää - J - + 4 k -k -
• b - = -Yllyttää + 0 -J - +7 k -k -

Ristituote niiden välillä lasketaan tunnistamalla ja korvaamalla vastaavat koordinaatit:

Voi palvella sinua: Hyperbolinen paraboloidi: Määritelmä, ominaisuudet ja esimerkit

-lla_x = 5; -lla_ja = −1; -lla_{z -z} = 4; b -_x = −1; b -_ja = 0: b_{z -z} = 7

-lla × b - = [(−1) ∙ 7 - 4 ∙ 0] Yllyttää + [(4 ∙ (−1) - 5 ∙ 7) J - + [5 ∙ 0 - (−1) ∙ (−1)] k -k - = [−7 - 0] Yllyttää + [(−4 - 35) J - + [0 - 1] k -k - =

= (−7) Yllyttää - 39 J - - k -k -

Determinant -menetelmä tarjoaa saman tuloksen.

Harjoittele

Laske determinantit, ristituote vektorien keskuudessa:

• tai = 2 Yllyttää +J - + 5 k -k -
• v = Yllyttää + 4J - +7 k -k -

Ja määritä edellisten vektorien rinnakkaisohjelman pinta -ala, kuten kuvassa esitetään:

Ratkaisu

Vektorien koordinaattien arvot korvataan determinantissa:

Määritetty rinnakkaisohjelma -alue on vektorituotteen moduuli niiden välillä, tuloksena: r = 17,3 alueyksiköt.