Merkittäviä tuotteita

Mitkä ovat merkittäviä tuotteita?

Merkittävät tuotteet ovat algebrallisia operaatioita, joissa ilmaistaan ​​polynomien kertolaskuja, joita ei tarvitse perinteisesti ratkaista, mutta tiettyjen sääntöjen avulla saman voidaan löytää.

Polynomit kerrotaan sen mukaan, onko siksi mahdollista, että heillä on paljon termejä ja muuttujia. Prosessin lyhytamiseksi käytetään merkittävien tuotteiden sääntöjä, jotka sallivat kertolaskut tarvitsematta mennä termille.

Merkittäviä tuotteita ja esimerkkejä

Jokainen merkittävä tuote on kaava, joka johtuu tekijästä, joka koostuu useiden termejen, kuten binomien tai trinomien polynomeista, joita kutsutaan tekijöiksi.

Tekijät ovat vallan perusta ja niillä on eksponentti. Kun tekijät lisääntyvät, eksponentit on lisättävä.

On olemassa useita merkittäviä tuotekaavoja, jotkut käytetään enemmän kuin toiset, polynomista riippuen, ja ovat seuraavat:

Neliömäinen

Se on binomiaalin kertominen itsessään, joka ilmaistaan ​​voiman muodossa, missä termit lisätään tai vähennetään:

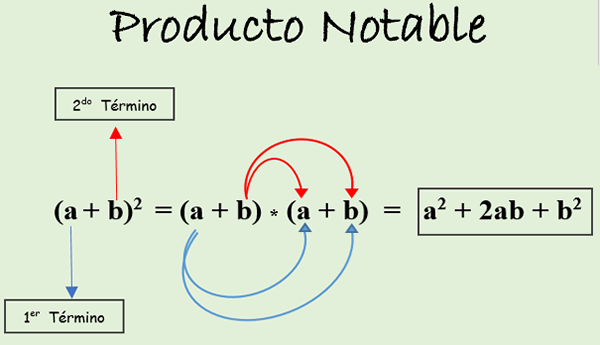
-lla. Neliömäinen binomiaalinen: Se on yhtä suuri kuin ensimmäisen termin neliö, plus kaksinkertainen termien tuote sekä toisen termin neliö. Se ilmaistaan ​​seuraavasti:

(A + B)² = (A + B) _* (A + B).

Seuraavassa kuvassa voit nähdä, kuinka tuote kehitetään edellä mainitun säännön mukaisesti. Tuloksena kutsutaan täydellisen neliön trinomialiksi.

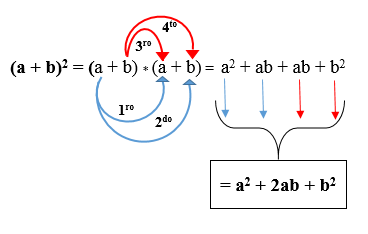
Esimerkki 1

(x + 5) ² = x² + 2 (x * 5) + 5²

(x + 5) ² = x² + 2 (5x) + 25

(x + 5) ² = x² + 10x + 25.

Esimerkki 2

(4a + 2b) = (4a)² + 2 (4 _* 2b) + (2b)²

(4a + 2b) = 8a² + 2 (8ab) + 4b²

(4a + 2b) = 8a² + 16 AB + 4B².

b -. Neliömäisen vähennysten binomi: Samaa summan binomiaalista sääntöä sovelletaan vain siihen, että tässä tapauksessa toinen termi on negatiivinen. Sen kaava on seuraava:

(A - b)² = [(a) + (- b)]²

Voi palvella sinua: Numeeriset analogiat: Tyypit, sovellukset ja harjoitukset

(A - b)² = a² +Toinen _* (-b) + (-b)²

(A - b)²   = a² - 2AB + B².

Esimerkki 1

(2x - 6)² = (2x)² - 2 (2x _* 6) + 6²

(2x - 6)²  = 4x² - 2 (12x) + 36

(2x - 6)² = 4x² - 24x + 36.

Konjugaatti binomials -tuote

Kaksi binomia on konjugoitu, kun kunkin toiset termit ovat erilaisia ​​merkkejä, ts. Ensimmäisen merkinnät ovat positiivisia ja toisen negatiivisen tai päinvastoin. Se ratkaistaan ​​nostamalla jokainen monomiaalinen neliö ja vähennetään. Sen kaava on seuraava:

(A + B) _* (A - b)

Seuraavassa kuvassa kehitetään kahden konjugoidun binomials -tuote, jossa havaitaan, että tulos on neliöiden ero.

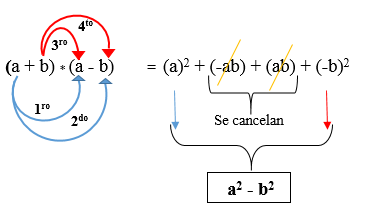
Esimerkki 1

(2a + 3b) (2a - 3b) = 4a² + (-6ab) + (6 AB) + (-9b²-A

(2a + 3b) (2a - 3b) = 4a² - 9B².

Kahden binomiaalin tuote, jolla on yhteinen termi

Se on yksi monimutkaisimmista ja vähän käytettyjä merkittäviä tuotteita, koska se on kahden binomin kertominen, joilla on yhteinen termi. Sääntö osoittaa seuraavan:

• Yhteisen termin neliö.
• Plus summa termit, jotka eivät ole yleisiä, ja kerro ne sitten yhteisella termillä.
• Plus niiden termien kertolaskujen summa, jotka eivät ole yleisiä.

Se on esitetty kaavassa: (x + a) _* (x + b) ja kehitetään kuvan osoittamalla tavalla. Tuloksena on epätavallinen neliömäinen trinomiaalinen.

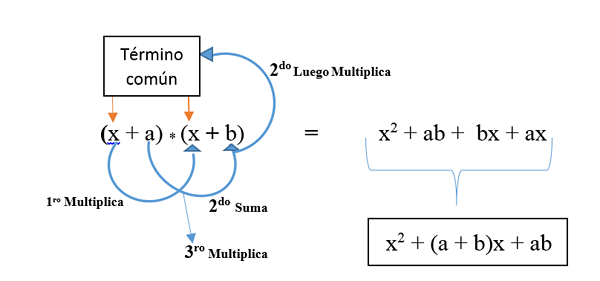Esimerkki 1

(x + 6) _* (x + 9) = x² + (6 + 9) _* X + (6 _* 9)

(x + 6) _* (x + 9) = x² + 15x + 54.

On mahdollista, että toinen termi (eri termi) on negatiivinen ja sen kaava on seuraava: (x + a) _* (x - b).

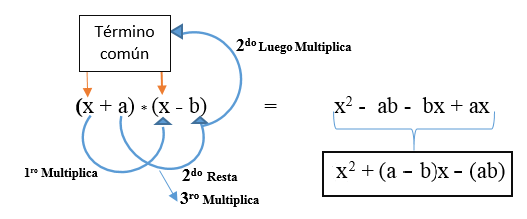
Esimerkki 2

(7x + 4) _* (7x - 2) = (7x _* 7x) + (4 - 2)_* 7x + (4 _* -2)

(7x + 4) _* (7x - 2) = 49x² + (2)_* 7x - 8

(7x + 4) _* (7x - 2) = 49x² + 14x - 8.

Voi myös olla niin, että molemmat eri termit ovat negatiivisia. Kaavasi on: (x - a) _* (x - b).

Voi palvella sinua: Lamy -lause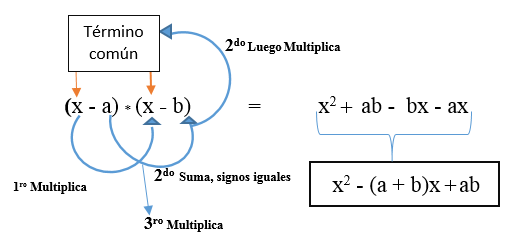

Esimerkki 3

(3b - 6) _* (3b - 5) = (3b _* 3b) + (-6 - 5)_* (3b) + (-6 _* -5)

(3b - 6) _* (3b - 5) = 9b² + (-yksitoista) _* (3b) + (30)

(3b - 6) _* (3b - 5) = 9b² - 33b + 30.

Neliömäinen polynomi

Tässä tapauksessa on enemmän kuin kaksi termiä ja sen kehittämiseksi jokainen leikataan ja lisää yhdessä kahdesti yhden termin kertolasku toisen kanssa; Sen kaava on: (A + B + C)² Ja operaation tulos on trinomiaalinen neliö.

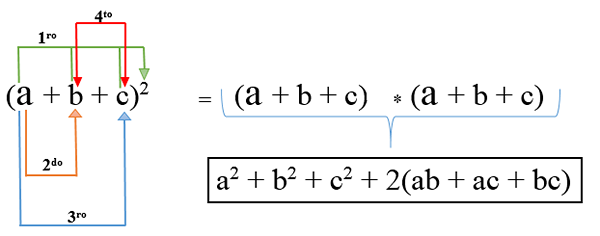
Esimerkki 1

(3x + 2y + 4z)² = (3x)² + (2 ja)² + (4Z)² + 2 (6xy + 12xz + 8yz)

(3x + 2y + 4z)² = 9x² + 4y² + 16Z² + 12xy + 24xz + 16yz.

Kuutiobinomi

Se on monimutkainen merkittävä tuote. Sen kehittämiseksi binomi kerrotaan neliöllä seuraavasti:

-lla. Summan kuutiolle binomialle:

• Ensimmäinen termi kuutio ja kolminkertainen ensimmäisen termin neliö toisella.
• Plus kolminkertainen ensimmäinen termi, toisella neliöllä.
• Plus toisen termin kuutio.

(A + B)³ = (A + B) _* (A + B)²

(A + B)³ = (A + B) _* (² + 2AB + B²-A

(A + B)³ = a³ + Toinen²B + AB² + ba² + 2AB² + b -³

(A + B)³ = a³ + Kolmas²B + 3AB² + b -³.

Esimerkki 1

(A + 3)³ = a³ + 3 (a)²_*(3) + 3 (a)_*(3)² + (3)³

(A + 3)³ = a³ + 3 (a)²_*(3) + 3 (a)_*(9) + 27

(A + 3)³ = a³ + 9 a² + 27a + 27.

b -. Vähennyksen kuutiolle binomialle:

• Ensimmäisen termin kuutio, paitsi ensimmäisen termin neliön kolminkertainen toisella.
• Plus kolminkertainen ensimmäinen termi, toisella neliöllä.
• Vähemmän toisen termin kuutio.

(A - b)³ = (a - b) _* (A - b)²

(A - b)³ = (a - b) _* (² - 2AB + B²-A

(A - b)³ = a³ - Toinen²B + AB² - ba² + 2AB² - b -³

(A - b)³ = -lla³ - Kolmas²B + 3AB² - b -³.

Esimerkki 2

(B - 5)³ = b³ + 3 (b)²_*(-5) + 3 (b)_*(-5)² + (-5)³

(B - 5)³ = b³ + 3 (b)²_*(-5) + 3 (b)_*(25) -125

Voi palvella sinua: Ryhmätiedot: Esimerkit ja liikunta ratkaistu

(B - 5)³ = b³ - 15b² +75b - 125.

Trinomiaalinen kuutio

Se kehittää sen kertomalla neliöllä. Se on erittäin laaja merkittävä tuote, koska kuutioon on nostettu 3 termiä, plus kunkin neliömäisen termin kolminkertainen, kerrottuna jokaisella termillä, plus kuusi kertaa kolmen termin tuote. Nähty paremmassa muodossa:

(A + B + C)³ = (A + B + C) _* (A + B + C)²

(A + B + C)³ = (A + B + C) _* (² + b -² + c² + 2AB + 2AC + 2BC)

(A + B + C)³ = A³ + b -³ + c³ + Kolmas²B + 3AB² + Kolmas²C + 3AC² + 3b²C + 3BC² + 6ABC.

Esimerkki 1

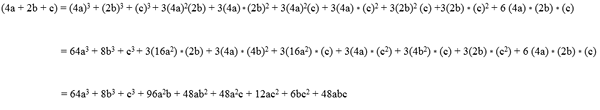
Ratkaistuja merkittäviä tuotteita

Harjoitus 1

Kehitä seuraava binomiaali kuutioon: (4x - 6)³.

Ratkaisu

Muistaminen, että kuutioon binomiaalinen on yhtä suuri kuin ensimmäinen kuutioon nostettu termi, lukuun ottamatta toisen termin neliön kolminkertaista; Plus kolminkertainen ensimmäinen termi, toisella neliöllä, paitsi toisen termin kuutio.

(4x - 6)³ = (4x)³ - 3 (4x)²(6) + 3 (4x) _* (6)² - (6)²

(4x - 6)³ = 64x³ - 3 (16x²) (6) + 3 (4x)_* (36) - 36

(4x - 6)³ = 64x³ - 288x² + 432x - 36.

Harjoitus 2

Kehitä seuraava binomiaalinen: (x + 3) (x + 8).

Ratkaisu

Sinulla on binomi, jossa on yhteinen termi, joka on X ja toinen termi on positiivinen. Sen kehittämiseksi vain yleistä termiä on nostettava, plus niiden termien summa, jotka eivät ole yleisiä (3 ja 8), ja kerrotaan ne sitten yhteisella termillä, plus termien kertolaskujen summa, jotka eivät ole yleisiä.

(x + 3) (x + 8) = x² + (3 + 8) x + (3_*8)

(x + 3) (x + 8) = x² + 11x + 24.

Viitteet

1. Enkeli, a. R -. (2007). Perusalgebra. Pearson -koulutus,.
2. Arthur Goodman, L. H. ( 1996). Algebra ja trigonometria analyyttisellä geometrialla. Pearson -koulutus.
3. S, s. (S.F.-A. Matematiikka plus 8. Yhdistynyt kuningaskunta: Sagar Ratna.
4. Jerome E. Kaufmann, K. Lens. (2011). Alkeis- ja keskitason algebra: Yhdistetty lähestymistapa. Florida: Cengage Learning.
5. Pérez, c. D -d. (2010). Pearson -koulutus.