Epälineaariset ohjelmointimenetelmät ja harjoitukset

Se Epälineaarinen ohjelmointi Useista riippumattomista muuttujista riippuu funktion optimointi, mikä puolestaan ​​on rajoitettuja rajoituksia.

Jos yksi tai useampi rajoitukset tai jos toiminto maksimoidaan tai minimoi (kutsutaan Objektiivitoiminto), ei ilmaista muuttujien lineaarisena yhdistelmänä, joten siellä on epälineaarinen ohjelmointiongelma.

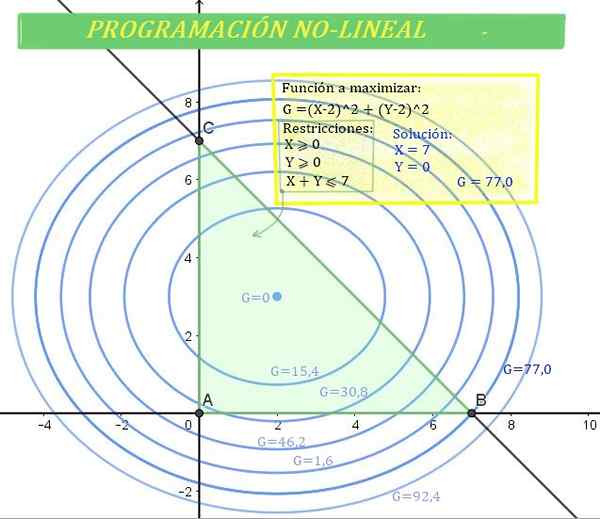
Kuvio 1. Epälineaarinen ohjelmointiongelma (NLP). jossa g on funktio (epälineaarinen), joka optimoida vihreällä alueella, määritettynä rajoituksilla. Lähde: f. Zapata.

Ja siksi lineaarisen ohjelmoinnin menettelyjä ja menetelmiä ei voida käyttää.

Esimerkiksi hyvin tunnettua menetelmää ei voida käyttää Simplex, joka pätee vain, kun objektiivifunktio ja rajoitukset ovat kaikki ongelman muuttujien lineaarinen yhdistelmä.

[TOC]

Lineaariset ohjelmointimenetelmät

Epälineaarisen ohjelmoinnin kannalta käytettävät tärkeimmät menetelmät ovat: 

1.- Graafiset menetelmät.

2.- Lagrange -kertoimet liuosalueen rajan tutkimiseksi.

3.- Gradientin laskenta objektiivifunktion päämäärien tutkimiseksi.

4.- Laskeutuvat vaiheet menetelmän löytää nollagradienttipisteet.

5.- Muokattu Lagrange-kertoimien menetelmä (Karush-Kuhn-Tuckerin kunnolla).

Esimerkki ratkaisusta graafisella menetelmällä

Esimerkki graafisen menetelmän ratkaisusta on se, mitä voidaan nähdä kuvasta 2:

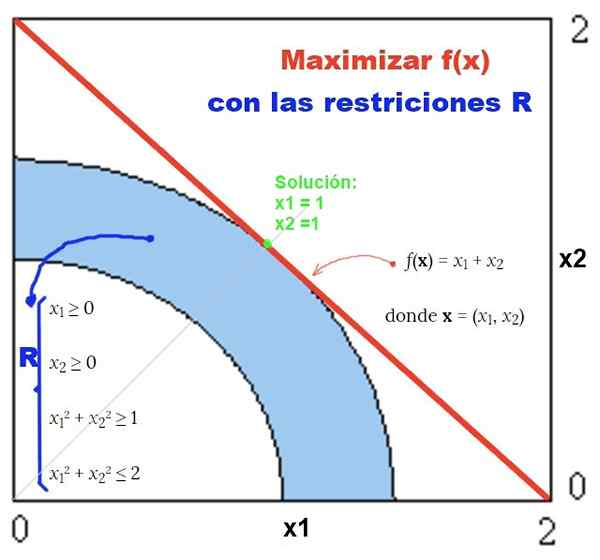Kuva 2. Esimerkki epälineaarisesta ongelmasta, jossa ei ole lineaalisia rajoituksia ja sen graafista ratkaisua. Lähde: f. Zapata.

Harjoitukset

- Harjoitus 1 (graafinen menetelmä)

Tietyn yrityksen voitto G riippuu tuotteen X myymästä määrästä ja tuotteen myymästä määrästä, ja lisäksi voitto määritetään seuraavalla kaavalla:

Voi palvella sinua: Konjugoidut binomial: miten se on ratkaistu, esimerkkejä, harjoituksia

G = 2 (x - 2)² + 3 (ja - 3)²

On tiedossa, että määrillä x ja y ovat seuraavat rajoitukset:

X ≥0; Y ≥0 ja x + ja ≤ 7

Määritä suurimman vahvistuksen tuottavien x: n ja y -arvot.

Kuva 3. Yrityksen voitto voidaan matemaattisesti mallintaa löytääkseen enimmäisvoitot epälineaarisella ohjelmoinnilla. Lähde: Pixabay.

Ratkaisu 

Tässä ongelmassa objektiivifunktio on epälineaarinen, kun taas rajoitukset määrittelevät eriarvoisuudet ovat. Se on ongelma Epälineaarinen ohjelmointi.

Tämän ongelman ratkaisemiseksi valitaan graafinen menetelmä.

Ensinnäkin ratkaisualue määritetään, mikä annetaan rajoituksilla.

Kuten x≥0; Y ≥0, ratkaisun on etsittävä XY -tason ensimmäisessä kvadrantissa, mutta koska lisäksi on täytettävä, että x + y ≤ 7, liuos on viivan x + y = 7 alemmassa puolipiljassa.

Liuosalue on ensimmäisen kvadrantin leikkaus linjan alemmalla puolisolulla, joka aiheuttaa kolmionmuotoisen alueen, jolla liuos sijaitsee. On sama kuin kuvassa 1 osoitetaan.

Toisaalta Gain G voidaan edustaa myös Cartesian tasolla, koska sen yhtälö on ellipsin kanssa keskustassa (2,3).

Ellipsi on esitetty kuvassa 1 useille G -arvoille. Korkeampi g, suurempi voitto.

On ratkaisuja, jotka kuuluvat alueelle, mutta eivät anna maksimiarvoa g, kun taas toiset, kuten g = 92.4, ovat vihreän vyöhykkeen ulkopuolella, toisin sanoen ratkaisuvyöhyke.

Sitten G: n maksimiarvo, niin että x e y kuuluu ratkaisualueelle vastaa: 

Voi palvella sinua: teoreettinen todennäköisyys: Kuinka saada se ulos, esimerkkejä, harjoituksia

G = 77 (maksimilehitys), joka tapahtuu x = 7 e y = 0. 

Mielenkiintoista on, että enimmäisvoitto tapahtuu, kun tuotemyynnin määrä on mitätön, kun taas tuotteen X määrä saavuttaa suurimman mahdollisen arvonsa.

- Harjoitus 2 (Analyyttinen menetelmä: Lagrange -kertoimet) 

Etsi ratkaisu (x, y), joka tekee funktiosta f (x, y) = x² + 2 ja² olla maksimaalinen alueella G (x, y) = x² + ja² - 1 = 0.

Ratkaisu

Se on selvästi epälineaarinen ohjelmointiongelma, koska sekä objektiivifunktio F (x, y) että rajoitus g (x, y) = 0, eivät ole muuttujien x ja y lineaarinen yhdistelmä.

Käytetään Lagrange -kerroinmenetelmää, joka vaatii ensin Lagrange L (x, y, λ) funktion määrittely:

L (x, y, λ) = f (x, y) - λ g (x, y) = x² + 2 ja² - λ (x² + ja² - 1) 

Missä λ on parametri, nimeltään Lagrange -kertoimen.

Objektiivifunktion F ääritarvojen määrittämiseksi rajoitusalueella G (x, y) = 0, näitä vaiheita noudatetaan:

-Etsi Lagrange L': n funktion osittaiset johdannaiset suhteessa x, y, λ.

-Nolla jokainen johdannainen.

Tässä näiden toimintojen järjestys:

1. ∂l/∂x = 2x - 2λx = 0
2. ∂l/∂y = 4y - 2λy = 0
3. ∂l/∂λ = -(x² + ja² - 1) = 0

Mahdolliset järjestelmäratkaisut

Tämän järjestelmän mahdollinen ratkaisu on λ = 1 ensimmäisen yhtälön tyydyttämiseksi, jolloin y = 0 vastaamaan toista.

Tämä ratkaisu tarkoittaa, että x = 1 tai x = -1 siten, että kolmas yhtälö on tyytyväinen. Tällä tavalla on saatu kaksi S1- ja S2 -ratkaisua:

S1: (x = 1, y = 0)

S2: (x = -1, y = 0).

Toinen vaihtoehto on, että λ = 2 toiselle yhtälölle täytettävästä arvosta riippumatta arvosta ja.

Se voi palvella sinua: Fermat -raja: mikä koostuu ja harjoitukset ratkaistu

Tässä tapauksessa ainoa tapa, jolla ensimmäinen yhtälö täyttyy, on, että x = 0. Kolmannen yhtälön huomioon ottaen on vain kaksi mahdollista ratkaisua, joita kutsumme S3: lle ja S4: lle:

S3: (x = 0, y = 1)

S4: (x = 0, y = -1)

Tiedät, mikä tai mitkä näistä ratkaisuista maksimoi objektiivifunktio, jatka korvaamaan f (x, y):

S1: F (1, 0) = 1² + 2.0 -² = 1

S2: F (-1, 0) = (-1)² + 2.0 -² = 1

S3: F (0, 1) = 0² + 2.1² = 2

S4: F (0, -1) = 0² + kaksikymmentäyksi)² = 2

Johtopäätöksenä on, että ratkaisut, jotka maksimoivat F, kun x ja y kuuluvat kehälle g (x, y) = 0 ovat S3 ja S4.

Arvoparit (x = 0, y = 1) y (x = 0, y = -1) maksimoivat F (x, y) liuosalueella G (x, y) = 0.

- Harjoitus 3 (nollagradientti)

Löydä ratkaisut (x, y) objektiivifunktiolle:

f (x, y) = x² + 2 ja²

Olla maksimaalinen alueella G (x, y) = x² + ja² - 1 ≤ 0.

Ratkaisu

Tämä harjoitus on samanlainen kuin harjoitus 2, mutta ratkaisualue (tai rajoitus) ulottuu ympärysmiilleen G (x, y) = 0, eli ympyrälle g (x, y) ≤ 0. Tähän sisältyy kehä ja sen sisäinen alue.

Rajaliuos määritettiin jo harjoituksessa 2, mutta on tarpeen tutkia sisäaluetta.

Tätä varten funktion f (x, y) gradientti on laskettava ja yhtä suuri kuin nolla, etsivät äärialueita liuosalueella. Tämä vastaa F: n osittaisten johdannaisten laskemista suhteessa X: ään ja vastaavasti ja tasoittaa nollaa:

∂f/∂x = 2 x = 0

∂f/∂y = 4 y = 0

Tällä yhtälöjärjestelmällä on ainoa ratkaisu (x = 0, y = 0), joka kuuluu ympyrälle g (x, y) ≤ 0.

Tämän arvon korvaaminen funktiossa f tulokset:

f (0, 0) = 0

Yhteenvetona voidaan todeta, että maksimiarvo, joka ottaa funktion liuosalueella.

 Viitteet

1. Avriel, m. 2003. Epälineaarinen ohjelmointi. Dover Publishing.
2. Bazaraa. 1979. Epälineaarinen ohjelmointi. John Wiley & Sons.
3. Bertsekas, D. 1999. Epälineaarinen ohjelma: 2. painos. Athena -tieteellinen.
4. Nocedal, J. 1999. Numeerinen optimointi. Springer-Verlag.
5. Wikipedia. Epälineaarinen ohjelmointi. Palautettu: on.Wikipedia.com