Summa assosiatiivinen omaisuus, kertolasku, esimerkit, harjoitukset

Se assosiatiivinen omaisuus summa edustaa operaation assosiatiivista luonnetta lisäävät erilaisia ​​matemaattisia sarjoja. Se yhdistää näiden sarjojen kolme (tai enemmän) elementtiä, nimeltään A, B ja C, niin että se on aina toteutunut:

A + (B + C) = (A + B) + C

Tällä tavoin on taata, että riippumatta siitä, kuinka ryhmittyä operaation suorittamiseen, tulos on sama.

Kuvio 1. Käytämme summan assosiatiivista ominaisuutta monta kertaa, kun teet aritmeettisia ja algebrallisia operaatioita. (Piirustus: Freepik -koostumus: F. Zapata)

Mutta on huomattava, että assosiatiivinen omaisuus ei ole synonyymi kommutatiiviselle omaisuudelle. Eli tiedämme, että lisäysjärjestys ei muuta summaa tai että tekijöiden järjestys ei muuta tuotetta. Joten summalle, jonka voit kirjoittaa näin: A + B = B + A.

Assosiatiivisessa ominaisuudessa se on kuitenkin erilainen, koska lisättävien elementtien järjestys ylläpidetään ja mitkä muutokset ovat ensin suoritetut operaatiot. Mikä tarkoittaa, että sillä ei ole merkitystä ensin (B+C) ja lisää tähän tulokseen, aloita lisääminen B: hen ja tulokseen lisää C C.

Monet tärkeät toiminnot, kuten summa ovat assosiatiivisia, mutta eivät kaikki. Esimerkiksi todellisten lukujen vähentämisessä tapahtuu, että:

A - (b - c) ≠ (a - b) - c

Kyllä a = 2, b = 3, c = 1, sitten: sitten:

2- (3 - 1) ≠ (2 - 3) - 1

0 ≠ -2

[TOC]

Yhdistymisen assosiatiivinen ominaisuus

Kuten summalle tehtiin, kertolaskujen assosiatiivinen ominaisuus osoittaa, että:

a ˟ (b ˟ c) = (a ˟ b) ˟ c

Voi palvella sinua: polynomien summa, kuten tehdään, esimerkkejä, harjoituksia

Real numerosarjan tapauksessa on helppo varmistaa, että se on aina. Esimerkiksi käyttämällä arvoja a = 2, b = 3, c = 1, sinun on:

2 _˟ (3 _˟ 1) = (2 _˟  3) _˟ 1 → 2 _˟ 3 = 6 _˟ 1

6 = 6

Todelliset numerot täyttävät sekä summan että kertolaskun yhdistävän ominaisuuden. Toisaalta toisessa sarjassa, kuten vektorien, summa on assosiatiivinen, mutta ristin tuote tai vektorituote ei ole.

Kertolaskujen assosiatiivisen ominaisuuden sovellukset

Etu siitä, että assosiatiivisen omaisuuden operaation on ryhmittynyt käteväimmällä tavalla toteutetaan. Tämä helpottaa suuresti ratkaisua.

Oletetaan esimerkiksi, että pienessä kirjastossa on 3 hyllyä, joissa kukin 5 viihdettä. Jokaisessa viihteessä on 8 kirjaa. Kuinka monta kirjaa on?

Voimme suorittaa operaation seuraavasti: Kokonaiskirjat = (3 x 5) x 8 = 15 x 8 = 120 kirjaa.

Tai niin: 3 x (5 x 8) = 3 x 40 = 120 kirjaa.

Kuva 2. Kertolaskennan assosiatiivisen ominaisuuden soveltaminen on laskea kirjojen lukumäärä jokaisessa hyllyllä. Kuva, jonka on luonut f. Zapata.

Esimerkit

-Luonnollisten, kokonaisten, rationaalisten, todellisten ja monimutkaisten lukujen sarjoissa summan ja kertolaskujen assosiatiivinen ominaisuus täyttyy.

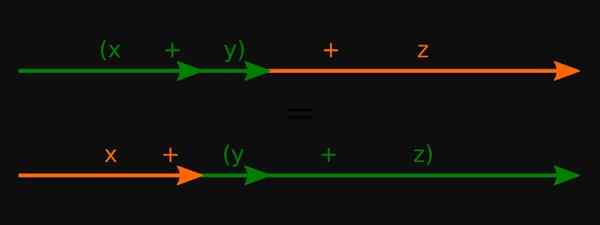Kuva 3. Reaalilukujen osalta summan assosiatiivinen ominaisuus täyttyy. Lähde: Wikimedia Commons.

-Polynomeihin niitä sovelletaan myös näihin operaatioihin.

-Vähennysoperaatioiden, jakamisen ja eksponentination tapauksissa assosiatiivista omaisuutta ei toteuteta reaalilukuina tai polynomeina.

Voi palvella sinua: Orthoedro: kaavat, alue, tilavuus, diagonaali, esimerkkejä

-Matriisien tapauksessa assosiatiivinen ominaisuus täyttyy summan ja kertolaskun suhteen, vaikka jälkimmäisessä tapauksessa kommutia ei täytetä. Tämä tarkoittaa, että matriisit A, B ja C on totta, että:

(A x b) x c = a x (b x c)

Mutta ... a x b ≠ b x a

Assosiatiivinen omaisuus vektoriin

Vektorit muodostavat erilaisen sarjan kuin reaalilukut tai kompleksiset numerot. Vektorisarjalle määritetyt toiminnot ovat jonkin verran erilaisia: on summa, vähennys ja kolmen tyyppiset tuotteet.

Vektorien summa kohtaa assosiatiivisen ominaisuuden, samoin kuin numerot, polynomit ja matriisit. Vektoreiden välillä tehdyt skalaarituotteet, vektorien ja ristin kiipeily, jälkimmäinen ei täytä, mutta skalaarituote, joka on toinen vektorien välinen toiminta, täyttää sen ottaen huomioon seuraavat:

-Vektorin skalaarin tuote johtaa vektoriin.

-Ja kiipeämällä kaksi vektoria, se on skalaari.

Siksi vektorit otetaan huomioon v, tai ja W -, Ja lisäksi skalaari λ, on mahdollista kirjoittaa:

-Vektorien summa: v +(tai + W - ) = (v + tai) + W -

-Skalaarituote: λ (v Olla tai ) = (λv) tai

Jälkimmäinen on mahdollista mitä v Olla tai Se on skalaari ja λv Se on vektori.

Kuitenkin:

v × (tai × W - ) ≠ (v × tai)×W -

Polynomitekijä ryhmittelemällä termejä

Tämä sovellus on erittäin mielenkiintoinen, koska kuten edellä todettiin, assosiatiivinen omaisuus auttaa ratkaisemaan tietyt ongelmat. Monomien summa on assosiatiivista ja tätä voidaan käyttää tekijään, kun ilmeinen yhteinen tekijä ei ilmesty ensi silmäyksellä.

Voi palvella sinua: Conpex Polygon: Määritelmä, elementit, ominaisuudet, esimerkit

Oletetaan esimerkiksi, että sitä pyydetään tekijä: x³ + 2x² + 3x +6. Tällä polynomilla puuttuu yleinen tekijä, mutta katsotaanpa mitä tapahtuu, jos se on ryhmitelty tällä tavalla:

x³ + 2x² + 3x +6 = (x³ + 2x²) + (3x +6)

Ensimmäisellä sululla on yleinen tekijä x²-

x³ + 2x² = x² (x+2)

Toisessa yhteisessä tekijässä on 3:

3x +6 = 3 (x + 2)

Niin:

x³ + 2x² + 3x +6 = x²(x+ 2)+ 3 (x+ 2)

Nyt on selvä yhteinen tekijä, joka on x+2-

x²(x+ 2)+ 3 (x+ 2) = (x+ 2) (x²+3)

Harjoitukset

- Harjoitus 1

Koulun rakennuksessa on 4 kerrosta ja jokaisessa on 12 luokkahuonetta, joissa on 30 työpöytää. Kuinka monta työpöytää koulussa on yhteensä?

Ratkaisu

Tämä ongelma ratkaistaan ​​soveltamalla kertolaskun yhdistävää ominaisuutta, katsotaan:

Työpyhien kokonaismäärä = 4 kerrosta x 12 luokkahuonetta /lattia x 30 työpöytä /luokkahuone = (4 x 12) x 30 työpöytä = 48 x 30 = 1440 työpöytää.

O, jos se on suositeltava: 4 x (12 x 30) = 4 x 360 = 1440 työpöytää

- Harjoitus 2

Polynomit:

A (x) = 5x³ + 2x² -7x + 1

B (x) = x⁴ +6x³ -5x

C (x) = -8x² +3x -7

Käytä summan assosiatiivista ominaisuutta löytääksesi (x) + b (x) + c (x).

Ratkaisu

Kaksi ensimmäistä voidaan ryhmitellä ja tulos lisää kolmannen:

A (x) + b (x) = [5x³ + 2x² -7x + 1] + [x⁴ +6x³ -5x] = x⁴ + 11x³+ 2x² -12x +1

Polynomi C (x) lisätään heti:

[x⁴ + 11x³+ 2x² -12x +1] + [-8x² +3x -7] = x⁴ + 11x³ - 6x² -9x -6

Lukija voi varmistaa, että tulos on identtinen, jos se on ratkaistu vaihtoehto A (x) + [b (x) + c (x)]]].

Viitteet

1. Jiménez, r. 2008. Algebra. Prentice Hall.
2. Matematiikka on hauskaa. Kommutatiiviset, assosiatiiviset ja piirit. Toipunut: Mathisfun.com.
3. Matematiikkavarasto. Määritelmä assosiatiivinen ominaisuus. Toipunut: Mathwarehouse.com.
4. Tiede. Lisäys- ja kertolaskujen assosiatiivinen ja kommutatiivinen ominaisuus (esimerkillä). Toipunut: tiedekunnasta.com.
5. Wikipedia. Assosiatiivinen omaisuus. Haettu: vuonna.Wikipedia.org.