Radikaalit

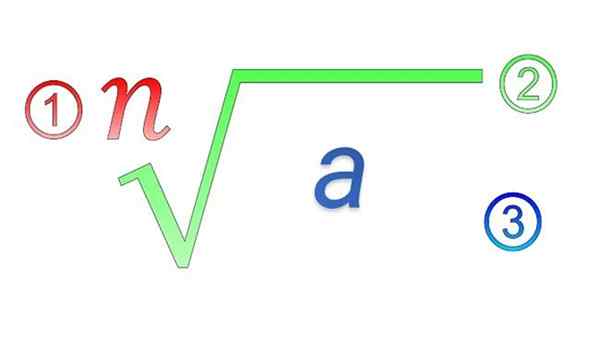
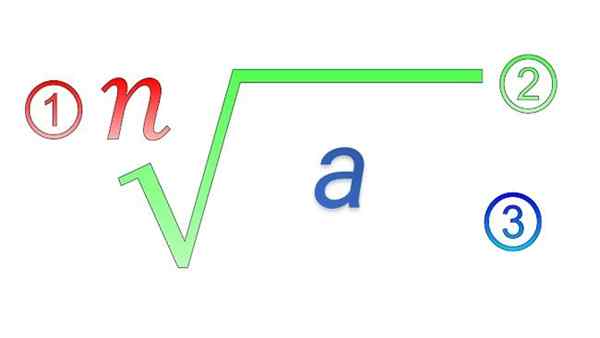Radikaalit elementit: 1) hakemisto; 2) radikaali symboli; 3) subradikaalinen määrä

Mitkä ovat radikaalien ominaisuudet?

Se radikaalit Ne ovat toimintoja, jotka mahdollistavat radikaalien ja voimien monimutkaisten ongelmien ratkaisemisen. Radikaali on tapa symboloida matemaattisesti määrän "a". Tämä juuri on toinen määrä, nimeltään "B", niin että sen nimi on tarkalleen "A", joten on pätevä kirjoittaa seuraava:

"N" -arvo on luonnollinen luku, joka tunnetaan nimellä juuri -indeksi "A" on Sädistävä tai subradical Määrä, ja "B" on "A" -jäänen n-. Sekä "A" että "B" kuuluvat todellisten lukujen joukkoon.

Jos hakemistoa ei ole kirjoitettu radikaalina, ymmärretään heti, että sen arvo on yhtä kuin 2 ja lukee A: n neliöjuuria.

Koska "N" kuuluu luonnollisten lukujen joukkoon, se voi olla pari tai pariton luku. Sitten seuraavat tapaukset erottuvat:

"N" par

• Jos A> 0 tai yhtä suuri kuin 0, A: n n-alcal juuri on positiivinen tai 0, ja sitä kutsutaan pääjuuri.
• Milloin < 0, no existe raíz n-ésima en el conjunto de los números reales, pero sí en los números complejos.

"N" outoon

• Kyllä A> 0, A-juuren n-Ede on positiivinen.
• Milloin< 0, la raíz n-ésima de “a” es negativa.

Joitakin esimerkkejä ovat seuraavat:

Kuvausominaisuudet

On mahdollista kirjoittaa määrä määrän määrää tehona, jolla on murto -eksponentti, ts.

Tässä tapauksessa juurihakemistosta tulee nimittäjä, kun taas subradikaalisen määrän eksponentista tulee osoittaja:

Voi palvella sinua: Homografinen toiminto: Kuinka kuvaaja, ratkaistut harjoitukset

Lauseke, joka on pätevä niin kauan kuin n ≠ 0, koska nimeäjän kanssa ei hyväksytä fraktioita.

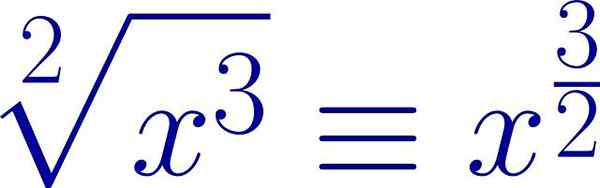Esimerkki radikaalista lausekkeesta, joka on kirjoitettu murto -eksponentin muodossa. Juuri -indeksi on eksponentin nimittäjä, kun taas lähetyksen voima on osoitus. Lähde: Wikimedia Commons.

Tällä tavoin voidaan käyttää samoja ominaisuuksia, joita sovelletaan voimiin, radikaalien tapauksessa.

Reaallukujoukkoon kuuluville arvoille nämä ominaisuudet ovat seuraavat:

1. Radikaali tuote, jolla on yhtä suuri indeksi

Saman indeksin kahden (tai useamman) radikaalin tuotteessa subradikaalit määrät kerrotaan, pitäen indeksi:

2. Saman hakemiston radikaali osuus

"A": n ja "B": n n-ENE: n, joka on B ≠ 0, välillä, on yhtä suuri kuin "A": n ja "B": n n-temeasy-juuret: "A" ja "B":

3. Juurijuuri

Määrän "A" M-EME: n N-Emeasy-juuren löytämiseksi subradikaali määrä kirjoitetaan juuren alla, jonka hakemisto on tuote "N": n ja "M": n välillä:

Menettely on helposti laajennettu peräkkäisiin sisäkkäisiin juuriin. Tuloksena oleva juurihakemisto on kaikkien indeksien, kuten tämä:

4. Juurien voima

N-THAT, nostettu Power M: lle, ilmaisee subradikaalin määrän mainitulle voimasta:

Erityiset tapaukset:

1) Kyllä n = m, Juurimerkki katoaa, jättäen pohjan nostettuksi voimaan 1:

Joka pätee ≥ 0. Yleensä, jos juurihakemisto on parillinen numero, sinulla on:

(Katso esimerkkejä myöhemmin)

2) Kyllä m> n, M/N -osuus on virheellinen ja juuria voidaan yksinkertaistaa, esimerkiksi etsimällä murto -osia, jotka vastaavat m/n siten, että osoittaja ja nimittäjä ovat serkkuja toistensa kanssa tai kirjoittamalla subradikaalista määrää ja soveltamalla joitain Tässä kuvatut ominaisuudet.

Voi palvella sinua: prismat ja pyramidit

(Katso esimerkkejä myöhemmin)

5. Radikaali monistus

Radikaali voidaan vahvistaa tekijällä Q -, Jos sekä juurihakemisto että subradikaalisen määrän teho, kerro mainitulla tekijällä, ja tämä operaatio ei tarkoita tuloksen muokkaamista. Siksi:

Edellyttäen, että ≥ 0, kun se on tasainen.

6. Tekijän käyttöönotto radikaalissa

Jos positiivinen “B” -kerroin kertoo radikaalia, se voi kulkea sen sisällä, jos se nousee samaan juurihakemistoon. Siinä tapauksessa:

7. Radikaalien summa ja vähennys

Radikaalit voivat lisätä ja vähentää, kunhan ne ovat sama indeksi ja niillä on sama subradikaali määrä.

Kun kaksi tai useampia radikaaleja on yhtä indeksi ja subradikaalinen määrä, sanotaan, että ne ovat Samankaltaiset radikaalit.

Esimerkiksi seuraavat radikaalit ovat samanlaisia:

Sen sijaan nämä radikaalit eivät ole samanlaisia, koska niillä ei ole samaa subradikaalista määrää:

Eivät myöskään nämä kaksi samanlaisia:

Koska radikaali indeksi ei ole sama.

Samanlaisia ​​radikaaleja voidaan vähentää yhdeksi, lisäämällä tai vähentämällä niitä seuraavia kertoimia.

Radikaalit ominaisuudet esimerkkejä

Esimerkki 1

Mikä on seuraavien juurten arvo?

32: n neliöjuuri löytyy suoraan laskimen avulla. Sen arvo on:

Suspensat osoittavat, että desimaalit ovat äärettömiä.

Jos et halua työskennellä desimaalilukujen kanssa, 32: n neliöjuuri voidaan myös laskea hajottamalla 32 sen ensisijaisissa tekijöissä:

32 = 2⁵

Tällä tavalla se saadaan:

Voi palvella sinua: 8: 8: Mitkä ovat helppoja selityksiä

Kirjoitettu murto -eksponentiksi:

Fraktio 5/2 on virheellinen, joten radikaalia voidaan yksinkertaistaa, käyttämällä voimien ominaisuuksia:

Nyt yllä oleva omaisuus 1:

Siksi:

Omalta osaltaan:

Siitä lähtien (−2)³ = −8.

Omaisuuden 4 mukaan:

Ja lopuksi, −8: n neliöjuuria ei ole reaalilukujen sarjassa, vaikkakin kompleksilukuja.

Esimerkki 2

Seuraava toimenpide:

Onko mahdollista vähentää tulosta?

Edellyttäen, että radikaalit ovat samanlaisia, on mahdollista vähentää niitä, mutta tällä on oltava sama indeksi ja sama subradikaali määrä. Edellisessä esimerkissä nähtiin, että:

Ensimmäisen lisäyksen kirjoittamiseen voidaan käyttää analogista menettelyä, jotta subradinen määrä on yhtä suuri:

Tämä radikaali on samanlainen kuin edellinen. Mitä tulee 81 neliöjuureen, tämä on 9, siksi:

Esimerkki 3

Mitä ominaisuuksia on tarpeen sovellettavaksi tämän toiminnan suorittamiseen?

Meidän on sovellettava ominaisuuksia 3 ja 5, jotka ovat vastaavasti juuren juuri ja radikaalin arvon käyttöönotto. Ensinnäkin omaisuus 5 sovelletaan ottamaan käyttöön “X”, joka on sisimmän juuren ulkopuolella:

Ja nyt lauseke on valmis soveltamaan omaisuutta 3 ja kerro kunkin radikaalin vastaavat indeksit:

Viitteet

1. Gonzales, D. 2011. Perusalgebra: teoria ja käytäntö. Toinen. Painos.
2. Haeussler, E. 2012. Ennakkoluulo. Ensimmäinen. Painos. Pearson.
3. Khan Acadaem. Eksponentit ja radikaalit. Toipunut: khanacademy.org.
4. Larson, r. 2012. Ennakkoluulo. Kahdeksas. Painos. Cengage -oppiminen.
5. Stewart, J. 2007. Matematiikka laskentaa varten. Viides. Painos. Cengage -oppiminen.