Yhdistelmä suhteellisuus selitys, kolme yhdistelmäsääntöä, harjoituksia

Se Komposiitti tai useita suhteellisuus Tietojen ja tuntemattomien välillä voidaan havaita suhde enemmän kuin kahden suuruuden välinen suhde, jossa suoraa ja käänteistä suhteellisuutta voidaan havaita. Se on edistyneempi versio yksinkertaisesta suhteellisuudesta, vaikka molemmissa menettelyissä käytetyt tekniikat ovat samanlaisia.

Esimerkiksi, jos 7 ihmistä tarvitaan lataamaan 10 tonnia tavaroita 3 tunnissa, yhdistettyjä suhteellisuutta voidaan käyttää laskemaan kuinka monta ihmistä tarvitaan 15 tonnin lataamiseen 4 tunnissa.

Lähde: Pixabay.com

Tähän kysymykseen vastaamiseksi on kätevää tehdä arvotaulukko arvioitavaksi ja yhdistääksesi suuruudet ja tuntemattomat.

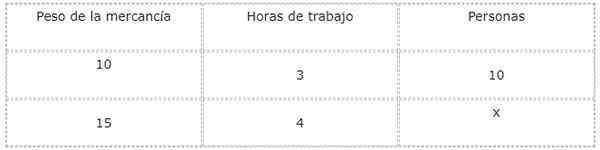
Analysoidaan kunkin suuruuden ja nykyisen tuntemattoman välisten suhteiden tyypit, mikä vastaa tässä tapauksessa ihmisten lukumäärää, jotka työskentelevät.

Kun tavaroiden paino kasvaa, myös ladattavien ihmisten lukumäärä kasvaa. Tämän vuoksi painon ja työntekijöiden välinen suhde on suora.

Toisaalta lisäämällä työntekijöiden lukumäärää, työajat vähenevät. Tämän vuoksi ihmisten ja työajan välinen suhde on käänteinen.

[TOC]

Kuinka laskea yhdisteiden suhteellisuudet

Edellisen esimerkkien ratkaisemiseksi käytetään enimmäkseen kolmea yhdisteen sääntömenetelmää. Tämä koostuu suuruuden ja tuntemattomien välisten suhteiden muodostamisesta ja tuotetta sitten fraktioiden välissä.

Alkuperäisen esimerkin suhteen arvotaulua vastaavat fraktiot järjestetään seuraavasti:

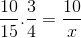
Mutta ennen kuin käänteistä suhdetta vastaavat fraktiot on käännettävä ennen tuntemattoman ratkaisemista ja puhdistamista. Että tässä tapauksessa vastaa aikimuuttujaa. Tällä tavoin ratkaiseva operaatio on:

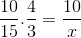
Jonka ainoa ero on muuttuvan ajanjaksoa 4/3 vastaavan osuuden sijoitus. X: n arvoa käytetään ja selkeä.

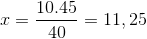
Siksi yli yksitoista ihmistä tarvitaan 15 tonnin tavaroiden lataamiseen 4 tunnissa tai vähemmän.

Selitys

Suhteellisuus on vakio suhde muutoksista, jotka ovat symmetrisiä jokaiselle kyseiselle suuruudelle. On suoraan ja käänteisesti suhteellisia suhteita, mikä määrittelee yksinkertaisen tai yhdistetyn suhteellisuuden parametrit.

Ohjaa kolme sääntöä

Se koostuu muuttujien välisestä suhteesta, joka sisältää saman käyttäytymisen muokattuna. Se on hyvin usein laskelmassa sadan eri suuruusprosentteja, joissa sen perusrakennetta arvostetaan.

Esimerkiksi voit laskea 15% 63: sta. Ensi silmäyksellä mainittua prosenttia ei voida nähdä yksinkertaisella tavalla. Mutta kolmen säännön täytäntöönpano voit tehdä seuraavan suhteen: jos 100% on 63, niin 15%, kuinka paljon se on?

Voi palvella sinua: tekijälause: Selitys, esimerkit, harjoitukset

100%-63

15%-X

Ja vastaava toiminta on:

(viisitoista% . 63) / 100% = 9,45

Jos prosenttimerkkejä yksinkertaistetaan ja 9,45 -luku, joka edustaa 15% 63: sta.

Kolme käänteistä sääntöä

Kuten nimestä voi päätellä, muuttujien välinen suhde on päinvastoin. Käänteinen suhde on luotava ennen laskelmaan jatkamista. Hänen menettelynsä on homologinen kolmen suoran säännön suhteen, lukuun ottamatta laskettavissa olevaan murto -osaan.

Esimerkiksi 3 maalaria tarvitsee 5 tuntia seinän loppuun saattamiseksi. Kuinka monta tuntia 4 maalaria päättyy?

Tässä tapauksessa suhde on käänteinen, koska lisäämällä maalareiden lukumäärää työajan tulisi vähentää. Suhde on vakiintunut;

3 maalaria - 5 tuntia

4 maalaria- x tuntia

Kun suhde on käänteinen, toimintajärjestys käännetään. Tämä on oikea tapa;

(3 maalaria) . (5 tuntia) / 4 maalarit = 3,75 tuntia

Termi maalarit yksinkertaistetaan ja tulos on 3,75 tuntia.

Kunto

Jotta yhdisteen tai monisuhdellisuuden läsnä ollessa on tarpeen löytää molemmat tyypit suuruuksien ja muuttujien välillä.

- Suora: Muuttuja on sama käyttäytyminen kuin tuntematon. Toisin sanoen lisäämällä tai vähentämällä sitä, toinen muuttuu tasa -arvoisesti.

- Käänteinen: Muuttuja esittelee antonymin käyttäytymisen tuntemattoman käyttäytymiseen. Osuus, joka määrittelee tämän muuttujan arvotaulukossa.

Tulosten todentaminen

On hyvin yleistä sekoittaa suuruusjärjestys työskennellessäsi yhdisteiden suhteellisuuksien kanssa, toisin kuin mitä tapahtuu tavanomaisissa osuuslaskelmissa, joiden luonne on enimmäkseen suoraa ja purkaa yksinkertaisen kolmen säännön avulla.

Siksi on tärkeää tutkia tulosten looginen järjestys, joka varmistaa kolmen yhdistetyssäännän heittämien lukujen koherenssi.

Alkuperäisessä esimerkissä tämän virheen tekeminen merkitsisi 20: n saamista seurauksena. Eli 20 ihmistä ladata 15 tonnia tavaroita 4 tunnissa.

Ensi silmäyksellä se ei tunnu hullulta tulokselta, mutta lähes 200%: n lisääntyminen henkilöstössä (7 - 20 henkilöstä) on utelias, kun tavaroiden lisääntyminen on 50%, ja jopa suuremmalla ajanjaksolla suorittaaksemme ajanjaksoa. tehdä työtä.

Se voi palvella sinua: Yleinen Parabola -yhtälö (esimerkit ja harjoitukset)

Tällä tavoin tulosten looginen todentaminen edustaa tärkeätä askelta toteuttamalla kolme yhdistelmäsääntöä.

Puhdistus

Vaikka lujamuoto on luonteeltaan matemaattisen muodostumisen suhteen, se on tärkeä askel suhteellisuustapauksissa. Virheellinen välys on riittävä mitä voidaan mitätöidä mikä tahansa tulos, joka saadaan kolmen yksinkertaisen tai yhdisteen järjestyksessä.

Historia

Kolmen sääntö tuli tunnetuksi lännessä arabien kautta, useiden kirjoittajien julkaisuilla. Heidän joukossaan al-Jwarizmi ja al-Biruni.

Al-Birunilla oli monikulttuurisen tiedonsa ansiosta pääsy laajoihin tietoihin tästä käytännöstä hänen Intian matkoissa, jotka olivat vastuussa laajimmasta dokumentaatiosta kolmesta kolmesta säännöstä.

Se herättää tutkimuksessaan, että Intia oli ensimmäinen paikka, jossa kolmen säännön käytöstä tehtiin yhteistä. Kirjailija varmistaa, että se tehtiin sujuvasti hänen suorassa, käänteisessä ja jopa koostuneissa versioissa.

Tarkka päivämäärä, jolloin kolmesta säännöstä tuli osa Intian matemaattista tietoa, ei ole vielä tiedossa. Bakhshalin käsikirjoitus löydettiin kuitenkin tähän käytäntöön suunnattu vanhin asiakirja vuonna 1881. Se on tällä hetkellä Oxfordissa.

Monet matematiikan historioitsijat varmistavat, että tämä käsikirjoitus on peräisin nykyisen aikakauden alusta.

Ratkaisut

Harjoitus 1

Lentoyhtiön on siirrettävä 1535 ihmistä. On tiedossa, että kolmella tasolla viimeisen matkustajan siirtäminen määränpäähän vie 12 päivää. 450 muuta ihmistä on saavuttanut lentoyhtiön ja 2 konetta on määrätty tekemään yhteistyötä tämän tehtävän kanssa. Kuinka monta päivää lentoyhtiö vie viimeiseen matkustajaan määränpäähänsä?

Ihmisten lukumäärän ja työpäivien välinen suhde on suora, koska mitä enemmän ihmisiä tarvitaan tämän työn suorittamiseen enemmän päiviä.

Toisaalta lentokoneiden ja päivien välinen suhde on käänteisesti verrannollinen. Lisäämällä lentokoneiden määrää tarvittavat päivät vähenevät siirtymiseen kaikille matkustajille.

Tätä tapausta viittaavat arvotaulukon taulukon.

Kuten alkuperäisessä esimerkissä on yksityiskohtainen, numerointi ja nimittäjä on sijoitettava käänteistä muuttujaa vastaavaan osuuteen tuntemattoman suhteen. Operaation jättäminen seuraavasti:

Voi palvella sinua: lähestymistapojen laskeminen erottelujen avulla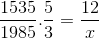

X = 71460/7675 = 9,31 päivää

Siirtymään vuoden 1985 ihmisiin, jotka käyttävät 5 tasoa, on tarpeen yli 9 päivää.

Harjoitus 2

25 -tonisen maissin sato viedään rahtikuorma -autoihin. On tiedossa, että edellisenä vuonna kesti 8 tuntia 150 työntekijän palkkalistoon. Jos palkanlaskenta kasvaa tänä vuonna 35%, kuinka kauan kuorma -autojen täyttäminen 40 -toniskorjuulla kestää?

Ennen arvotaulukon edustamista tämän vuoden työntekijöiden lukumäärä on määritettävä. Tämä kasvoi 35% 150 työntekijän alkuperäisestä luvusta. Tätä varten käytetään suoraa kolme sääntöä.

100% - 150

35% - x

X = (35 . 100)/100 = 52,5. Tämä on ylimääräisten työntekijöiden lukumäärä edellisen vuoden suhteen, ja se saa 203 työntekijän kokonaismäärän, mikä on tyytymätöntä saadun määrän pyöristämiseen.

Vastaava tietotaulukko on määritelty

Tässä tapauksessa paino edustaa suoraa suhdemuuttujaa tuntemattoman ajan kanssa. Toisaalta työntekijöiden muuttuja hallitsee käänteistä suhdetta ajan kanssa. Suurempi määrä työntekijöitä, päivä on lyhyempi.

Kun nämä näkökohdat otetaan huomioon ja sijoittavat työntekijöitä vastaavaa osaa, se lasketaan.

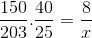
X = 40600/6000 = 6,76 tuntia

Päivä kestää vähän alle 7 tuntia.

Ehdotetut harjoitukset

- Määritä 73% 2875: stä.

- Laske tuntien määrä, jonka Teresa nukkuu, jos tiedetään, että vain 7% päivän kokonaismäärästä. Määritä kuinka monta tuntia nukkuu viikossa.

- 2000 julkinen sanomalehti 5 tunnin välein, käyttämällä vain 2 tulostuskonetta. Kuinka monta kopiota tuottaa 1 tunnissa, jos käytät 7 konetta? Kuinka kauan tuottaa 10.000 kappaletta 4 konetta käyttämällä?

Viitteet

1. Encyclopedia Alvarez-INICIACION. -Lla. Álvarez, Antonio Álvarez Pérez. EDAF, 2001.
2. Täydellinen alkuaine ja erinomainen ensisijainen ohje käsikirja: Hakijoiden käyttö opettajille ja erityisesti normaalien maakuntien koulujen oppilaille, osa 1. Joaquín Avendaño. Tulostaminen d. Dionisio Hidalgo, 1844.
3. Real -toimintojen arviointi. P. P. Petrushev, Vasil Atanasov Popov. Cambridge University Press, 3. maaliskuuta. 2011.
4. Alkuperäiset aritmeettiset opettamiseen Keski -Amerikan kouluissa ja kouluissa. Darío González. Kärki. Areenales, 1926.
5. Matematiikan tutkimus: matematiikan tutkimuksesta ja vaikeuksista. Augustus de Morgan. Baldwin ja Cradock, 1830.