Mikä on tehtävän ponnistus ja miten se saadaan?

Hän Tuottopyrkimys Se määritellään välttämättömäksi ponnisteluksi, jotta esine alkaa muodonmuutoksen pysyvästi, ts. Muovisen muodonmuutoksen kokemukset rikkomatta tai murtumista.

Koska tämä raja voi olla hiukan epätarkka joillekin materiaaleille ja käytettyjen laitteiden tarkkuus on painokerroin, tekniikassa on määritetty, että metallien, kuten rakennesterästen, siirtotoimet ovat yksi, joka tuottaa 0.2% pysyvä muodonmuutos esineessä.

Kuvio 1. Rakenteilla käytetyillä materiaaleilla on testata, kuinka paljon vaivaa ne kykenevät vastustamaan. Lähde: Pixabay.

Tuottopyrkimyksen arvon tunteminen on tärkeää tietää, onko materiaali sopiva käytölle, jonka haluat antaa sen kanssa valmistetuille osille. Kun pala on muodonmuutos joustavan rajan ulkopuolella, se ei ehkä pysty suorittamaan oikein toimintoa, johon se oli tarkoitettu, ja se on vaihdettava.

Tämän arvon saamiseksi testit suoritetaan yleensä materiaalilla (näytteillä tai näytteillä) tehdyillä näytteillä, joille altistetaan erilaisia ​​ponnisteluja tai kuormia, kun taas heidän kokeneensa pidennys tai venytys. Nämä testit tunnetaan nimellä Vetokokeet.

Vetokokeen suorittamiseksi voima käynnistetään tyhjästä ja lisää arvoa vähitellen, kunnes näyte on rikki.

[TOC]

Ponnistelut käyrät

Pitoskokeella saadut dataparit kuvaavat kuormitusta pystysuoraan akseliin ja vaakasuoran akselin muodonmuutokset. Tulos on alla esitetty kaavio (kuva 2), jota kutsutaan materiaalin ponnistelujen muodostumiskäyräksi.

Siitä määritetään monia tärkeitä mekaanisia ominaisuuksia. Jokaisella materiaalilla on oma ponnistelu-EFFOR-käyrä. Esimerkiksi yksi tutkituimmista on rakenneteräs, jota kutsutaan myös makeaksi tai vähähiiliseksi teräsksi. Se on materiaali, jota käytetään laajasti rakentamisessa.

Se voi palvella sinua: valo: historia, luonto, käyttäytyminen, eteneminen

Pyrkimyksenkäyrällä on erottuvia alueita, joilla materiaalilla on jonkin verran käyttäytymistä käytetyn kuorman mukaan. Sen tarkka muoto voi vaihdella huomattavasti, mutta silti niillä on joitain yleisiä ominaisuuksia, jotka on kuvattu alla.

Sillä seuraava kuva 2, joka vastaa hyvin yleisesti rakenteellista terästä.

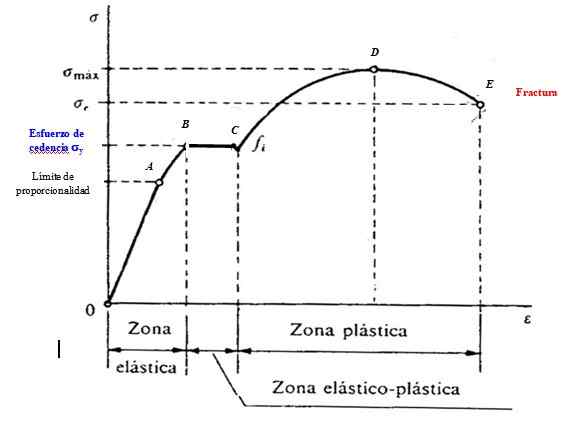Kuva 2. Teräspyrkimyskäyrä. Lähde: Modifioitu HANS TOPO1993 [CC BY-SA 3.0 (https: // creativecommons.Org/lisenssit/by-SA/3.0)]

Joustava alue

Alue, joka siirtyy tai A: lle, on joustava alue, jolla Hooken laki on pätevä, jossa ponnistus ja muodonmuutos ovat verrannollisia. Tällä alueella materiaali on täysin talteen otettu ponnistelujen levittämisen jälkeen. Kohta A tunnetaan suhteellisuusrajaksi.

Joissakin materiaaleissa käyrä, joka menee O A: sta A A: sta, ei ole linja, mutta silti niitä ei ole olemassa joustavaksi. Tärkeää on, että he palauttavat alkuperäisen muodonsa, kun kuorma lakkaa.

Elast-muovinen vyöhyke

Sitten meillä on A - B -alue, jolla muodonmuutos kasvaa nopeammin ponnisteluilla ja lakkaa olemasta molemmat suhteellisia. Käyrän kaltevuus vähenee ja B muuttuu vaakasuoraan.

Kohdasta B materiaali ei enää palauta alkuperäistä muotoa, ja katsotaan, että ponnistelujen arvo tuolloin on Cencia -ponnistelu.

Aluetta, jota B: stä C: hen kutsutaan materiaalin sato- tai hiipimiseksi. Siellä muodonmuutos jatkuu, että kuorma ei kasva. Se voi jopa vähentyä, joten sanotaan, että tässä tilassa oleva materiaali on Täydellinen muovi.

Muovinen alue ja murtuma

Alueella, joka siirtyy C: stä D: hen, muodonmuutoksella on kovettuminen, jossa materiaalilla on muutoksia rakenteessaan molekyyli- ja atomitasolla, mikä pyrkii enemmän välttämättömien muodonmuutosten saavuttamiseen.

Voi palvella sinua: Moody kaavio: Yhtälöt, mitä se on, sovellukset

Siksi käyrä kokee kasvun, joka päättyy saavutettaessa enimmäistyötä σ_Max.

D: stä E: hen on edelleen mahdollista muodonmuutosta, mutta vähemmän kuormituksella. Näytteessä (näyte) muodostuu eräänlainen oheneminen nimeltään tiukka, joka lopulta johtaa siihen pisteeseen, että E havaitsi murtuman. Kohdassa D materiaalia voidaan kuitenkin pitää rikki.

Kuinka saada siirtopyrkimys?

Joustava raja L_ja materiaalista on suurin vaivaa, joka voi kestää menettämättä joustavuutta. Se lasketaan osamäärällä maksimivoiman F suuruuden välillä_m ja näytteen ristikkäinen alue.

Lens_ja = F_m /

Kansainvälisen järjestelmän elastiset rajayksiköt ovat N/M² tai pa (Pascal), koska se on vaivaa. Joustava raja ja suhteellisuusraja pisteessä A ovat hyvin läheisiä arvoja.

Mutta kuten alussa todettiin, niitä ei ehkä ole helppo määrittää. Pyrkimysmuodostuskäyrän kautta saatu tuotto on käytännöllinen lähestymistapa tekniikan elastiseen rajaan.

Cedencian ponnistelut ponnistelujen muodostumiskäyrästä

Tämän saamiseksi viiva vedetään yhdensuuntaisen linjan kanssa, joka vastaa elastista aluetta (joka noudattaa Hooken lakia), mutta siirretty noin 0.2% vaaka -asteikolla tai 0.002 PLG / tiedot.

Tämä viiva ulottuu käyrän leikkaamiseen pisteessä, jonka pystysuuntainen koordinaatti on tuottoponnistuksen haluttu arvo, nimeltään σ_ja, Kuten kuvasta 3 voidaan nähdä. Tämä käyrä kuuluu toiseen taipuisaiseen materiaaliin: alumiiniin.

Voi palvella sinua: Kineettinen energia: Ominaisuudet, tyypit, esimerkit, harjoitukset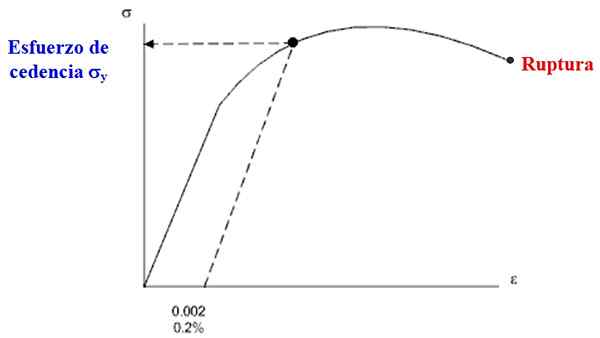Kuva 3. Pyrkimyskäyrä - alumiinin muodonmuutos, josta siirtopyrkimykset määritetään käytännössä. Lähde: Itse tehty.

Kahdella pallokella olevalla materiaalilla, kuten teräs ja alumiini, on erilaiset ponnistelukäyrät. Esimerkiksi alumiini ei esiinny terästä suunnilleen vaakasuoraa osaa, joka voidaan nähdä edellisessä osassa.

Muut hauraita materiaaleja, kuten lasia, eivät käy yllä kuvattujen vaiheiden läpi. Repeämä tapahtuu kauan ennen huomattavia muodonmuutoksia.

Tärkeät yksityiskohdat, jotka otetaan huomioon

- Periaatteessa tarkasteltuihin ponnisteluihin ei oteta huomioon muutosta, jota epäilemättä tuotetaan näytteen poikkileikkauksen alueella. Tämä indusoi pienen virheen, joka korjataan piirtämällä Todelliset ponnistelut, Ne, jotka ottavat huomioon alueen vähentämisen, kun näytteen muodonmuutos kasvaa.

- Tarkasteltavat lämpötilat ovat normaaleja. Jotkut pallokeittimet alhaisissa lämpötiloissa lakkaavat olemasta, kun taas toiset herkkyydet käyttäytyvät siunauslaitteina korkeammissa lämpötiloissa.

Viitteet

1. Olut, f. 2010. Materiaalimekaniikka. McGraw Hill. Viides. Painos. 47-57.
2. Reuna -insinöörit. Tuottolujuus. Toipunut.com.
3. Ryömimispyrkimykset. Palautettu: Instron.com.AR
4. Valera Negrete, J. 2005. Yleiset fysiikan muistiinpanot. Yksinäinen. 101-103.
5. Wikipedia. Hiipiä. Toipunut: Wikipedia.com