Mikä on rhombuksen ja suorakulmion välinen suhde?

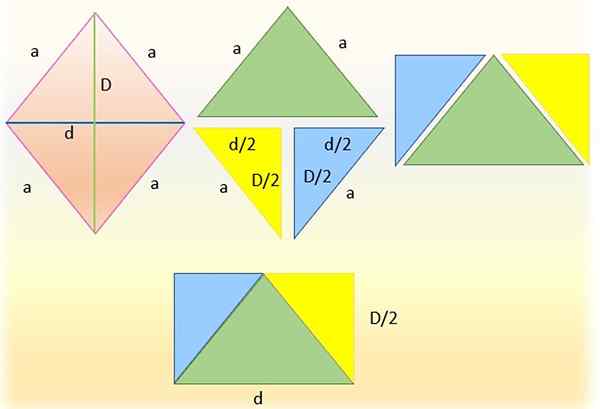
Rhombus hajottaa suorakulmion saamiseksi. Lähde: f. Zapata

Rhombus -alue (ja jotkut muut geometriset kuviot) on mahdollista laskea kolmion tai siihen liittyvän kvadrilateraalisen, kuten rinnakkaisgrammin tai suorakulmion pinta -alalta.

Suorakulmion ja rinnakkaisohjelman pinta -ala on sama: se on laskettu kuvan pohjan ja sen korkeuden välisen tuotteena kyseisen pohjan suhteen. Kolmion alue puolestaan ​​on puoliksi tuote sen pohjan ja sen korkeuden välillä.

Nämä kaavat on helppo muistaa, vaikka luonnollisesti geometria tarjoaa yksinomaisen kaavan rhombus -alueelle, tietäen sen pää- ja vähäisten diagonaalien mitta, joka on merkitty D ja D, vastaavasti:

Tämä ekspressio on mahdollista päätellä yllä olevassa kuvassa esitetyn sekvenssin kautta.

Tätä varten vasemmalla oleva rhombus leikataan yhdellä sen diagonaalista, joka tehtiin kuviossa, joka leikataan pienellä diagonaalilla, jolloin saatiin kaksi kolmiota. Yläkolmio (vihreänä) on vasemmalle ja alempi on jaettu vuorostaan ​​kahteen kolmioon, leikkaamalla puoleen tärkeimmistä diagonaaleista, saaden kolmiot suorakulmiot identtisen sinisen ja keltaisen.

Sitten näiden kolmioiden hypoteenit ovat samaan aikaan vihreän kolmion sivujen kanssa, koska ne mittaavat saman, eli ". Ja lopulta saadaan suorakulmio, jonka pohja on alempi D -diagonaali ja jonka korkeus on puolet suurimmasta diagonaalista, ts. “D/2”.

Suorakulmioalue muodostuu siten samaan aikaan täsmälleen rhombuksen alueelle, joten voidaan vahvistaa, että:

Voi palvella sinua: Trinomial

-Lla _timantti = (pohja × korkeus) _suorakulmio = D × (d/2)

Tulos, joka, kuten voidaan nähdä, tapahtuu täsmälleen ennen annetun Rhombus -alueen kaavan kanssa.

Rombo- ja rinnakkaisohjelma -alue

Rhombus. Esimerkiksi seuraavassa kuvassa vasemmalla on rhombus ja oikealla oleva rinnakkainen.

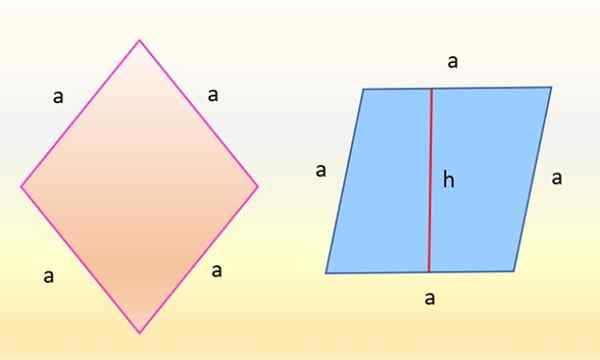Vasemmalla puolella oleva Rhombus -alue on sama kuin oikealla oleva rinnakkainen. Lähde: f. Zapata

Osoittautuu, että luvut ovat identtisiä, koska se, mikä on muuttunut, on vain suuntaus. Vasemmalla puolella oleva Rhombus, vaaleanpunainen, jonka sivuilla on sama mitta: A, se on käännetty siten, että yksi sen sivuista on täysin vaakasuora. Sitten rhombus muodostaa sinisen rinnakkaisgrammin oikealla puolella.

Ja tämän rinnakkaisohjelman pinta -ala on myös tuote "A": n ja sen korkeuden välissä suhteessa kuvaan "H", siksi: siksi:

-Lla _suunnikas = × H

Koska se on sama luku, alue on identtinen ja seuraa sitä:

-Lla _timantti = × H

Siten, tietäminen ja h suuntarammion, sen pinta -ala on laskettu ja se vastaa rhombuksen aluetta.

Rombo -alue, joka on kirjoitettu suorakulmioon

Toinen suhde Rhombuksen ja suorakulmion välillä ilmestyy, kun ensimmäinen on rekisteröity toisen sisällä. Jos näin tapahtuu, Rhombus -kärjet ovat samanlaisia ​​suorakulmion sivujen keskipisteen kanssa, joka näytetään alla:

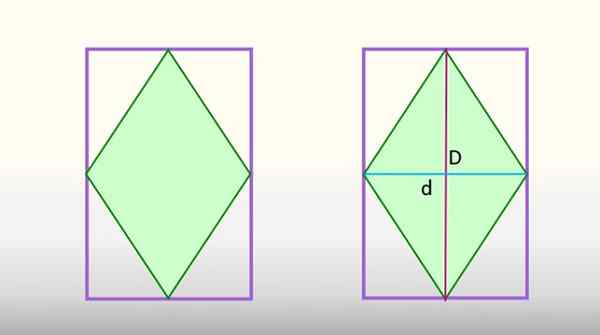Suorakulmioon kirjoitettu rhombus -alue vastaa puolta suorakulmion alueesta. Lähde: f. Zapata

Tämä määräys tekee rhombuksen pää- ja vähäiset diagonaalit, kuva on jaettu 8 identtiseen kolmioon, joista 4 vastaa Rhombusta, vihreänä ja muut 4 ovat osa suorakulmiota. Jos nämä viimeiset 4 kolmiota liittyvät yhteen, ne muodostavat puolet suorakaiteen ja 4 rhombus -kolmiosta, toisesta.

Se voi palvella sinua: Iskosceles -kolmio

Siksi Rhombus -alue vastaa puolta suorakulmion alueesta, jolla se on rekisteröity, ja toteaa:

-Lla_timantti = A_suorakulmio / 2

Tämä varmennetaan helposti laskemalla yhden kolmioiden pinta -ala ja kertomalla 4: llä, koska ne ovat identtisiä. Minkä tahansa kolmion pinta -ala on puolet tuotteesta pohjan ja sen korkeuden välillä:

-Lla _kolmio = pohja × korkeus /2

Edellisestä kuvasta havaitaan, että yhden kolmion pohja on D/2 ja korkeus on D/2, joka korvaa edellisessä kaavassa: antaa:

-Lla _kolmio = (d /2) × (d /2) /2 = (d × d) /8

Kertomalla tämä tulos 4: llä, jolla on rhombus -alue:

-Lla _timantti = 4 (d × d) /8 = (d × d) /2

Suorakulmion puoli puolestaan ​​on:

-Lla _suorakulmio / 2 = pohja × korkeus / 2

Koska suorakulmion pohja on D ja sen korkeus on D, se pysyy:

-Lla_suorakulmio / 2 = d × d/ 2

Joka on juuri rekisteröidyn rhombuksen alue. Silloin päättyy:

Suorakulmiossa rekisteröidyn rhombuksen pinta -ala vastaa puolta tämän alueesta.

Ratkaisut

Harjoitus 1

Paljon.6 cm ja alempi diagonaali 9.8 cm?

Ratkaisu

Korvaamalla d = 14.6 cm ja d = 9.8 cm Rhombus -alueen kaavassa:

Haettu alue on:

-Lla _timantti = 14.6 cm × 9.8 cm = 143.1 cm²

Harjoitus 2

Edellisen osan kuvassa suorakulmiossa rekisteröidyn rhombuksen tärkein diagonaali mitat ovat d = 30 cm ja suorakulmion alue on 210 cm: n arvoinen². Sitä pyydetään laskemaan:

a) Pienen diagonaalin pituus

Se voi palvella sinua: Line- ja Semi -River -segmentti

b) Rhombus -alue, kahdella tavalla: ensimmäinen suorakulmion alueen läpi ja toinen käyttämällä rhombuksen alueen kaavaa. Tarkista, että tulos on sama.

Liittää jhk

Suorakulmioalue on tuote sen pohjan ja sen korkeuden välillä. Suurin diagonaali on sen korkeus, kun taas pienin diagonaali D olisi pohja. Aluekaavan käyttäminen ja lausunnon arvojen korvaaminen, sinulla on:

-Lla _suorakulmio = pohja × korkeus = d × 30 cm = 210 cm²

Sitten pohja on arvoinen:

D = 210 cm² / 30 cm = 7 cm

Ratkaisu b

Kuten edellä nähdään, Rhombus -alue on puolet suorakulmion alueesta, ja tämä tiedetään:

-Lla _timantti = 210 cm² /2 = 105 cm²

Tulos tarkistetaan välittömästi korvaamalla kaava:

Diagonaalit tunnetaan jo: D = 30 cm, d = 7 cm, sitten:

-Lla _timantti = 30 cm × 7 cm /2 = 105 cm²

On todistettu, että odotetusti Rhombus -alue on sama molemmissa tapauksissa.