Syy muutokseen

Mikä on muutoksen syy?

Se Syy muutokseen Se on matemaattinen suuruus, joka määrittelee muuttujan tai fyysisen suuruuden muutoksen toisen suhteen. Esimerkiksi nopeus on syy sijainnin muuttamiseen ajankohtana.

Muutos suuruudessa x, Se on merkitty kreikkalaisten sanoitusten Δ (se lukee ”delta”) ja on kirjoitettu Δx. Se lasketaan lopullisen ja alkuperäisen arvon välisellä erolla: Δx = x_lopullinen- x_alkukirjain.

Jos suuruus x liittyy toiseen suuruuteen ja, Tämä kokee myös muutoksen, nimeltään Δy = y_lopullinen- ja_alkukirjain, Syy Y: n muuttamiseen X: n suhteen on määritelty osamääräksi:

Mikä on aiemmin ilmoitettuna Delta -merkinnän käyttäminen, pysyy näin:

Tämä osamäärä tunnetaan nimellä Osamäärä - ja kunnioittaen x jompikumpi Keskimääräinen tai keskimääräinen muutossuhde.

Tällä tavalla voit määritellä suuruudet, kuten väestön kasvuindeksi, nopeus, jolla esine, työttömyysaste, vesivirta putken läpi ja monet muut. Kaikki nämä määrät ovat käytännössä muutoksen syitä.

Miksi on tärkeää laskea muutoksen syy?

Lukuisat mielenkiintoiset suuruudet eivät pysy muuttumattomia, vaan kokevat muutoksia, ja usein nämä muutokset seuraavat toisiaan ajoissa. Siten merkitys laskettavan syyn muuttamiseen ajan myötä.

Esimerkiksi on yksinkertainen tapaus, joka liikkuu suoraa linjaa pitkin, joka voi olla vaakasuora akseli tai akseli x. Mobiili (auto, polkupyörä, henkilö, joka kävelee tai juoksee ...) muuttaa jatkuvasti asemaansa ajan kuluessa t.

Sitten syy objektin Δx sijainnin muuttamiseen aikavälillä Δt, tunnetaan nimellä keskimääräinen nopeus:

Toinen matkapuhelin, joka kulkee saman suoran linjan läpi, voi tehdä sen erilaisella nopeudella, riippumatta siitä, ja tällä tavalla se erotetaan ensimmäisestä mobiililaitteesta (koska se on hitaampi tai nopeampi).

Esimerkiksi 100 metrin tasaisella käytävällä on keskimääräinen valuuttakurssi asemaansa paljon suurempi kuin maratonilainen tai henkilö, joka kävelee hiljaa kadulla.

Nopeus on tyypillinen esimerkki muutossuhteesta, mutta joitain mielenkiintoisia suuruuksia, jotka myös kokevat muutoksia ajassa.

Tietäen muutoksen syyt, voit tietää paljon tapaa, jolla nämä suuruudet kehittyvät ajan myötä.

Yksiköt muutoksen syystä

Suhde on kahden suuruuden välinen suhde, tuloksena olevat yksiköt ovat myös niiden mittaamiseen käytettyjen yksiköiden osuus. Esimerkiksi nopeus on ajan pituus, koska se on syy sijainnin muuttamiseen ajan suhteen.

Tällä tavoin nopeusyksiköt voivat olla metrejä/sekunti, kilometriä tunnissa, mailia/tunti ja monet muut yhdistelmät.

Kuinka muutos syy lasketaan?

Keskimääräinen syy tai valuuttakurssi kahden suuruuden välillä lasketaan helposti, kun suoritetaan osamäärä kunkin vastaavien variaatioiden välillä, kaavan mukaan:

Muutokset suuruudessa voidaan antaa varastotaulukoiden kautta tai määrittää kaaviolla, jonka vastaavat arvot ja ja x (Katso lopussa ratkaistu harjoitus).

Toisaalta:

Ja oikean ilmaisun ilmaisu on juuri viivan kaltevuus, jonka päätelty on, että keskimääräinen muutoksen syy on Secant -viivan kaltevuus Y: n kaavioon X riippuen X: stä.

Merkit muutoksen syystä

Annetun määritelmän mukaan muutoksen syy voi olla positiivinen tai negatiivinen riippuen siitä, kuinka kyseiset suuruudet vaihtelevat, koska ne voivat kasvaa tai vähentää, mukaan.

Jos muutoksen syy on positiivinen, se tarkoittaa, että muutokset ja ja sisään x Ne olivat sama merkki, toisin sanoen, ja lisääntynyt ja x Hän teki myös. Tai niin paljon ja kuten x He vähenivät.

Kuitenkin, kun muutos syy on negatiivinen, se tarkoittaa kuitenkin, että yksi suuruuksista kasvoi ja toinen laski.

Välitön muutos syy

Usein se on paljon mielenkiintoisempaa. Tässä tapauksessa on välttämätöntä, että ΔX -variaatio on erittäin pieni, taipumus 0: een (mutta ilman 0, koska jakautumista 0 välillä ei ole määritelty).

Tätä kutsutaan "rajan ottamiseen", ja siinä tapauksessa hetkellisen muutoksen suhdetta kutsutaan "johdannaiseksi" ja kunnioittaen x ja se on merkitty dy/dx; Niin:

Suhde tai hetkellinen muutosnopeus on myös yhtä suuri kuin viivan kaltevuus, mutta tässä tapauksessa se on tangentin viivan kaltevuus kuvaajaan ja vastaan x.

Yksinkertaiset esimerkit

Ihmisen kasvu

Heidän syntymisensä jälkeen lapset kasvavat tahdissa, jotka määritetään useiden tekijöiden perusteella, joista genetiikka ja ruoka erottuvat. Korkein kasvuvauhti esiintyy ensimmäisen elämän vuoden aikana; Myöhemmin, lapsuudessa ja sitten murrosiässä, lapset yleensä kokevat "venyvyyttä", ts. Syy korkeuden muutokseen ajan suhteen ja vähennä sitten sitten.

Puberteettin jälkeen pojat kasvavat edelleen, mutta nopeus laskee, kunnes ne peruutetaan, kun he saavuttavat lopullisen aikuistensa.

Kahvikahvi viileä

On tunnettu tosiasia, että kahvi tai kuuma keitto jäähdytetään vähitellen huoneenlämpötilassa. Jäähdytysnopeus kuitenkin hidastaa kahvin lämpötilan tai keittoa huoneenlämpötilassa.

Yksi tapa mallintaa tämä ilmiö on läpi Newtonin jäähdytyslaki, Sen mukaan nopeus, johon lämpö siirretään. Suhteellisuusvakio k on ominainen aineelle:

T_jompikumpi edustaa ympäristölämpötilaa.

Ratkaisut

Harjoitus 1

Laske keskimääräinen muutossuhde ja kunnioittaen x, Seuraavat arvot:

ja₁ = 3; ja₂ = 10; x₁ = 2; x₂ = 5

Ratkaisu

Kaavan mukaan:

Lauseessa annetut arvot korvataan ja operaatio ratkaistaan:

Harjoitus 2

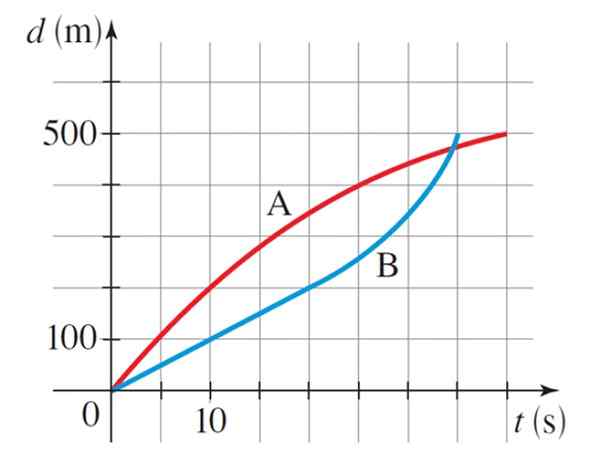
Kaavio näyttää vastaavat etäisyyskäyrät kahden olympiakisanopeuden A ja B ajan 500 metrin modaalisuudessa. Kuka voitti kilpailun? Mikä oli kunkin luistelijan keskimääräinen nopeus?

Ratkaisu

Kraafia tarkkailemalla seuraa, että luistelija B (sininen käyrä) voitti kilpailun, koska se kiertää 500 metriä 35 sekunnissa, kun taas luistelija A (punainen käyrä) teki niin 40 sekunnissa.

Vastaavat keskimääräiset nopeudet olivat:

Viitteet

1. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Osa 1. Kinematiikka. Toimittanut Douglas Figueroa (USB).
2. Glencoe -tiede. Muutos- ja kaltevuus (2021). Toipunut: Glencoe.com.
3. Larson, r. (2012). Ennakkoluulo. Kahdeksas. Painos. Cengage -oppiminen.
4. Larson, r. (1986). Laskenta analyyttisellä geometrialla, toinen. Painos. McGraw-Hill.
5. Stewart, J. (2011). Korkeakoulun algebra, käsitteet ja kontekstit. Brooks/Cole.