Trigonometriset syyt esimerkkejä, harjoituksia ja sovelluksia

Se trigonometriset syyt Ne ovat osia tai syitä, jotka voidaan tehdä oikean kolmion sivujen arvolla. Nämä puolet ovat: kaksi luokkaa, jotka muodostavat 90º toistensa kanssa, ja hypotenuse, joka muodostaa akuutin kulman θ yhdellä luokalla.

6 ajakot voidaan muodostaa. Heidän nimensä ja vastaavat lyhenteet ovat:

• Rinta (Sen)
• Coseno (cos)
• tangentti (TG tai Tan)
• Kotangentti (CTG tai COTAN)
• Secante (Sec) ja
• Harmonia (harmonia)

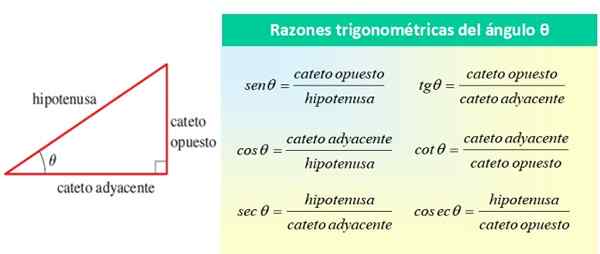
Ne kaikki viittasivat kulmaan θ, kuten seuraavassa kuvassa esitetään:

Kuvio 1. Akuutin kulman θ trigonometriset syyt. Lähde: f. Zapata.

Kulman θ perus- trigonometriset syyt ovat sin θ, cos θ ja tan θ, kun taas loput syyt voidaan ilmaista näiden kolmen suhteen. Edellisestä kuvasta näet sen:

• Sec θ = 1/ cos θ
• haittaa θ = 1/ sin θ
• pinnasänky θ = 1/tg θ

Kolmion sivujen koko ei vaikuta syiden arvoon, koska kaksi kolmiota, joiden kulmat mittaavat samat, ovat samanlaisia ​​kolmioita ja vastaavilla osuuksilla sivujen välillä on sama arvo.

[TOC]

Esimerkki

Lasketaan esimerkiksi kulman θ trigonometriset syyt seuraavissa kolmioissa:

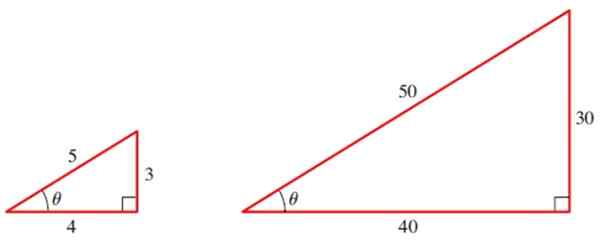Kuva 2. Kahdella samanlaisella kolmiolla on samat trigonometriset syyt heidän kulmistaan. Lähde: Stewart, J.Precculment: Laskentamatematiikka.

Pienelle kolmiolle meillä on kolme kulman perussyistä θ:

sin θ = 3/5

cos θ = 4/5

tg θ = ¾

Ja nyt lasketaan kolme θ: n perussyistä ison kolmion kanssa:

sin θ = 30/50 = 3/5

cos θ = 40/50 = 4/5

Tg θ = 30/40 = ¾

Tärkeä huomioitava yksityiskohta on seuraava: Sekä sin θ että cos θ ovat vähemmän kuin 1, koska luokat mittaavat aina vähemmän kuin hypotenuse. Todellakin:

sin θ = 3/5 = 0.6

cos θ = 4/5 = 0.8

Ratkaisut

Seuraavissa harjoituksissa pyydetään ratkaisemaan oikea kolmio, mikä tarkoittaa sen kolmen sivun pituuden ja sen sisäkulmien mittauksen löytämistä, joista yksi mittaa aina 90º.

Voi palvella sinua: Ensimmäisen aseman yhtälöt: kaava, kuinka ratkaista ne, esimerkki, harjoitukset

Pythagoras -lause koskee suorakaiteen kolmioita ja on erittäin hyödyllinen, kun kaksi sivua tunnetaan ja puuttuva on määritettävä. Lause sanoo:

Hypotenuusa² = vastapäätä Catetoa² + viereinen Cateto²

Voimme tarkistaa Pythagoras -lauseen kuvan 2 pienellä kolmiolla, jonka jalat ovat 3 ja 4. Luokkien ottamisjärjestyksellä ei ole merkitystä. Lauseen soveltaminen:

Hypotenuusa² = 3² + 4² = 9 + 16 = 25

Siksi hypotenuse on:

Hypotenuse = √25 = 5

- Harjoitus 1

Laske seuraavien kolmioissa esitettyjen kulmien trigonometriset syyt:

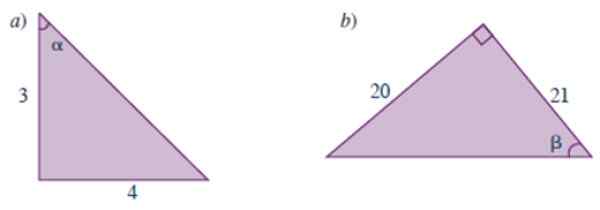Kuva 3.- Vuoden kolmiot ratkaistiin 1. Lähde: Carena, M. 2019. Preuniversity -matematiikan käsikirja.

Liittää jhk

Tämä kolmio on sama kuvassa 3, mutta he kysyvät meiltä toisen akuutin kulman trigonometriset syyt, merkitty α. Lausunto ei tarjoa hypotenusan arvoa soveltamalla Pythagoras -lausetta, jonka tiedämme, että sen arvo on 5.

Syyt voidaan laskea suoraan määritelmästä ja varovainen valittaessa jalkaa, joka on kulman α vastapäätä sen laskemiseksi sen α: n laskemiseksi. Katsotaan:

• synti α = 4/5
• cos α = 3/5
• TG α = 4/3
• pinnasänky α = ¾
• SEC α = 1/(3/5) = 5/3
• haittaa α = 1/(4/5) = 5/4

Ja kuten näemme, trigonometristen syiden arvot on vaihdettu. Itse asiassa α ja θ ovat täydentäviä kulmia, mikä tarkoittaa, että ne lisäävät 90º. Tässä tapauksessa on toteutettu, että sen α = cos θ ja niin edelleen muista syistä.

Ratkaisu b

Lasketaan kolmion hypotenuse Pythagoras -lauseen läpi:

Hypotenuusa² = 20² + kaksikymmentäyksi² = 841

√841 = 29

Sitten kulman β 6 trigonometristä syytä ovat:

• SEN β = 20/29
• cos β = 21/29
• TG β = 20/21
• Pinnasänky β = 21/20
• SEC β = 1/(21/29) = 29/21
• haittaa β = 1/(20/29) = 20/29

Voi palvella sinua: yhdistetyt toiminnot

- Harjoitus 2

a) Löydä X: n arvo kuvasta.

b) Laske esitetyn 3 kolmion kehä.

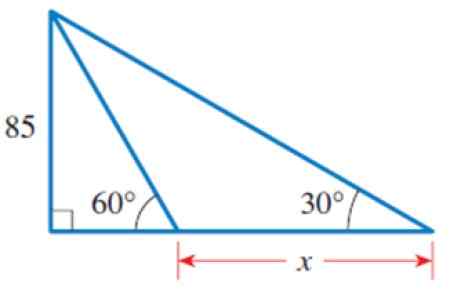Kuva 4. Vuoden kolmiot ratkaistiin 2. Lähde: Stewart, J. Precculment: Laskentamatematiikka.

Liittää jhk

Kuvassa voimme tunnistaa useita kolmioita, erityisesti vasemman suorakulmion kolmio, jonka luokka on yhtä suuri kuin 85 ja akuutti kulma 60º.

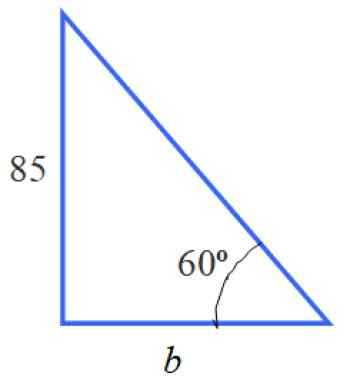Kuva 5. Vasemmalla oleva kolmio.

Tämän kolmion tietojen avulla voimme laskea sivun B. Se ei ole toimenpide, jota lausunto kysyy, mutta sen arvon tietäminen on edellinen vaihe.

Asianmukaisen syyn määrittämiseksi on TG 60 º = 85 /B, koska B on 60 °: n vieressä oleva jalka ja 85 on päinvastainen kuin mainittu kulma. Siksi:

B = 85 / Tg 60º = 85 / √3

Kun tunnet B: n, käytämme suurta ja ulkoista suorakulmiokolmiota, jolla on yhteinen puoli edellisen kolmion kanssa: se, joka mittaa 85. Tämä on Cateto, joka vastustaa 30º kulmaa.

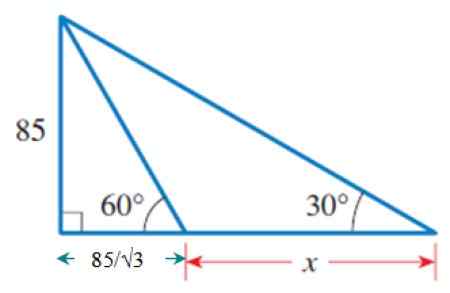Kuva 6. Ulompi kolmio, josta osa pohjasta on jo tiedossa.

Sieltä:

Cateto, joka on 30º = (85/√3) + x

Nyt voimme nostaa seuraavan:

85 / [(85 / √3) + x] = tg 30º

Mikä on neliömäissä, kerrotaan 30º TG:

85 = [(85/√3) + x]. TG 30º

Kertolaskun jakautuvan ominaisuuden soveltaminen:

85 = TG 30º. (85/√3) + x. TG 30º

Siksi:

x.TG 30º = 85 - TG 30º. (85/√3) = 85 [1 - TG 30º . (1/√3)] = 85 . (2/3) = 170/3

TG -arvon korvaaminen 30º = √3 / 3:

x = (170/3) ÷ (√3 / 3) = 98.viisitoista

Ratkaisu b

Pienen kolmion kehä

Olla h₁ Tämän kolmion hypotenuse, joka voidaan laskea Pythagoras -lauseella tai trigonometrisen syyn kautta, esimerkiksi COS 60º:

cos 60 º = 85 / √3 / h₁→ H₁ = (85/√3) ÷ cos 60º = 98.1

Löydäksesi P, tämän kolmion kehä, lisäämme vain 3 sivua:

Voi palvella sinua: Kuvailevat tilastot: historia, ominaisuudet, esimerkit, käsitteet

P = 85 + (85/√3) + 98.1 = 232.2

Ulkoisen kolmion kehä

Olla h₂ Ulkoisen kolmion hypotenusiin:

SEN 30º = 85 ÷ H₂  

h₂ = 85 ÷ sin 30º = 170

Tälle kolmiolle kehä on:

P = 85 + [(85/√3) + 98.15] + 170 = 402.22

Ei -suoritetun kolmion kehä

Tästä kolmiosta tunnemme jo kaikki sen sivut:

P = x + h₁ + h₂ = 98.15 + 98.15 + 170 = 366.3

Trigonometristen syiden sovellukset

Trigonometriset syyt ovat lukuisia käytännön sovelluksia, esimerkiksi korkeus voidaan laskea.

Oletetaan, että vesitorni on 325 metrin päässä rakennuksesta. Ikkunassa sijaitseva tarkkailija Huomaa, että tornin yläpään korkeuskulma on 39 º, kun taas tornin pohja näkyy 25º. Ihmeet:

a) mikä on tornin korkeus?

b) kuinka paljon ikkuna on?

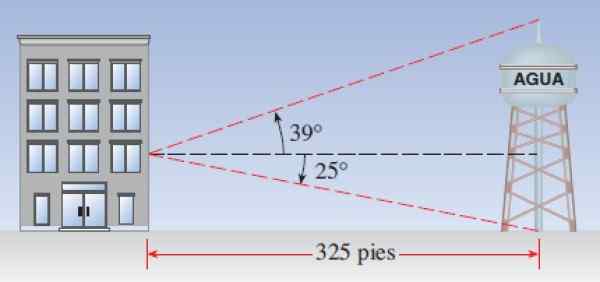Kuva 7. Kaavio Vista Torren korkeuden laskemiseksi rakennuksesta. Lähde: Stewart, J. Precculment: Laskentamatematiikka.

Liittää jhk

Yläkolmion 39 vastapäätä olevasta katetosta saamme osan vastauksesta:

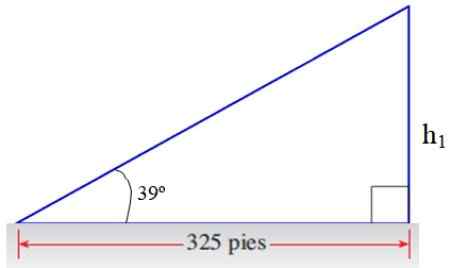Kuva 8. Kolmio levitysharjoitteluun. Lähde: f. Zapata.

h₁/325 = TG 39º → H₁ = 325 . TG 39º jalkaa = 263.2 jalkaa

Samalla tavalla saamme loput tornin korkeudesta, nimeltään h₂ Alemmasta kolmiosta:

h₂/325 = TG 25º → H₂ = 325 . TG 25º jalkaa = 151.6 jalkaa

Tornin kokonaiskorkeus on h₁ + h₂ = 263.2 + 151.6 jalkaa = 414.7 jalkaa.

Ratkaisu b

Ikkuna on tarkasti korkeudessa h₂ Maa:

h₂ = 151.6 jalkaa.

Viitteet

1. Carena, m. 2019. Preuniversity -matematiikan käsikirja. Rannikon kansallinen yliopisto.
2. Hoffman, J. Matematiikan aiheiden valinta. Osa 3.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Stewart, J. 2006. Precculment: Laskentamatematiikka. Viides. Painos. Cengage -oppiminen.
5. Zill, D. 1984. Algebra ja trigonometria. McGraw Hill.