Tavallisen ja epäsäännöllisen Pentagonin alue, miten se otetaan, harjoitukset

Laskea Pentagonin alue Ensin meidän on selvitettävä, onko tämä säännöllinen vai ei. Pentagon on monikulmio, viiden sivun suljettu litteä kuva. Kun monikulmio on säännöllinen, se tarkoittaa, että sen sivujen pituus on sama ja myös sen sisäkulmat.

Tällöin on kaava tavallisen monikulmion tarkan alueen laskemiseksi, tietäen joitain sen pääominaisuuksista, jotka päätämme myöhemmin.

Kaksi Pentagonia

Jos monikulmio ei ole säännöllinen, ts. Siinä on erikokoisia ja epätasa -arvoisia sisäkulmia, ei ole yhtä kaavaa.

Matemaatikot ovat kuitenkin löytäneet laskentastrategioita, kuten hahmon jakaminen muihin, joilla on alhaisin sivu, kuten kolmiot, neliöt ja suorakulmiot, joiden mitat ovat tiedossa tai helposti laskettuna.

Toinen menettely monikulmioiden alueiden laskemiseksi, sen kärkipisteiden koordinaattien tuntemiseksi, on menetelmä, jota kutsutaan Gauss -determinantit, että kuvaamme myöhemmin.

[TOC]

Kuinka laskea tavallisen Pentagonin pinta -ala?

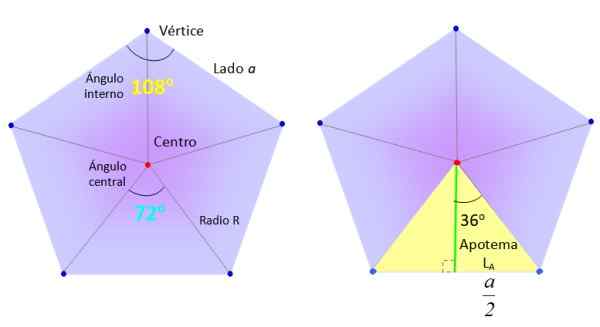
Aiomme ottaa tavallisen viisikunnan sivulta A, ja jaamme sen viiteen yhtä suureen kolmioon, kuten kuvassa esitetään, piirtäen segmenttejä keskustasta (punaisesta) kärjistä (sininen).

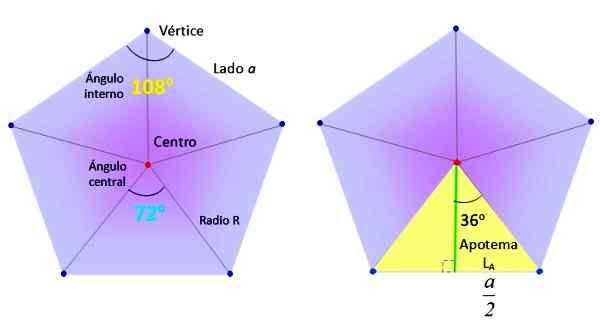Tarvittavat elementit tavallisen Pentagonin alueen löytämiseksi. Lähde: f. Zapata.

Kolmiot puolestaan, kuten ylemmän kuvan oikealla puolella oleva keltainen keltainen, jaetaan kahteen yhtä suureen suorakulmioon, nimeltään vihreän segmentin ansiosta apoteemi.

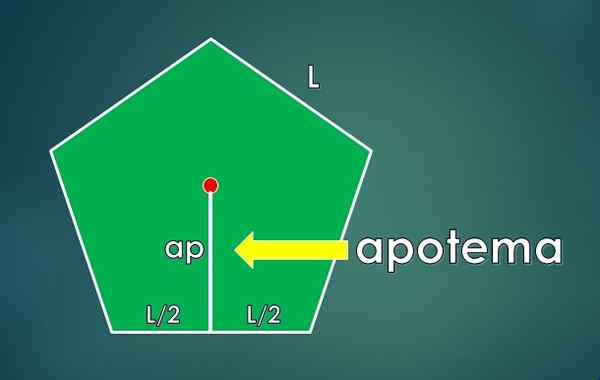
ApoTeme määritellään kohtisuoraan segmentiksi, joka yhdistyy monikulmion keskustaan ​​toisen puolen keskustaan. Sen pituus on L_-Lla.

Pohja A/2: n ja korkeuden L: n suorakulmion kolmion alue_-Lla On:

[(A/2) x l_-Lla-

Pentagonissa on 10 tällaista kolmiota, joten sen alue on:

Voi palvella sinua: vektoritoiminnot

A = 10 (a/2) x l_-Lla

Mutta kehä P Pentagonista on tarkalleen p =10a, Siksi alue annetaan kehän osittain tuote ja apoteemin pituus:

A = p x l_-Lla /2

Säännöllinen Pentagonin alue tuntemalla sivu a

Ilmaisee apoteemin l: n pituuden_-Lla Sivusta A riippuen tietäen, että osoitettu kulma on puolet keskikulmasta, eli 36º, vastaa:

36º = π/5

Alkuaineen trigonometria, akuutin kulman 36º tangentti:

Tan (π/5) = (a/2) ÷ l_-Lla

Siten:

Lens_-Lla=  (A/2) ÷ rusketus (π/5)

Korvaaminen edellisessä osassa vähennettynä alueella ja tietäen, että p = 5a:

A = p x l_-Lla /2

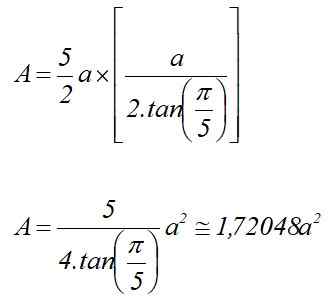
Säännöllinen Pentagonin alue tietää radionsa

Hän radio Tavallisen monikulmio on segmentti, joka siirtyy keskustasta yhteen sen kärjessä. Se tapahtuu samanaikaisesti rajoitetun kehän säteen kanssa, kuten seuraavassa kuvassa esitetään:

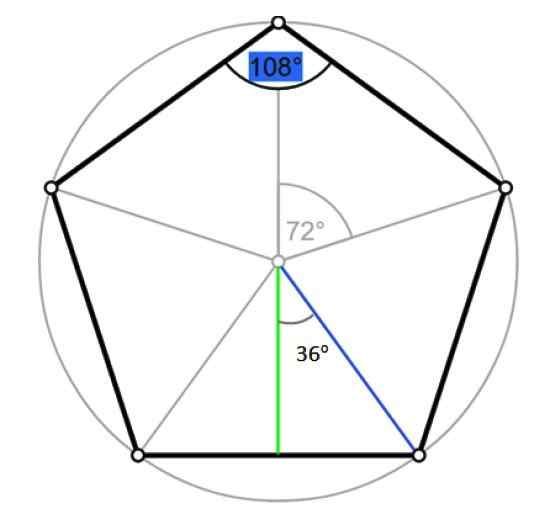Pentagonin kulmat ja apoteemit. Lähde: Wikimedia Commons/F. Zapata.

Olkoon r mainitun radion mitta, joka osuu samaan aikaan edellisessä kuviossa rajattu oikean kolmion hypotenusia sinisellä. Trigonometrialla:

cos 36º = cos (π/5) = l_-Lla ÷ r

JA

sin 36º = sin (π/5) = (a/2) ÷ r

Siksi:

A = p x l_-Lla /2 = 5R. synti (π/5) x r. cos (π/5) = 5r² [sin (π/5) x cos (π/5)]]

Kaksoiskulman kaavan käyttäminen:

sin (2θ) = 2 sen θ . cos θ

Meidän täytyy:

[sin (π/5) x cos (π/5)] = (1/2) sin 72º,

Ja niin korvaamalla tämä arvo saadaan seuraavan kaavan tavalliselle Pentagonin alueelle:

A = (5/2) r².Sen 72º

Kuinka laskea epäsäännöllisen pentagonin pinta -ala?

Kuten olemme aiemmin sanoneet, epäsäännölliselle monikulmiolle ei ole yhtä kaavaa, mutta on olemassa kaksi menetelmää, jotka yleensä toimivat erittäin hyvin, ensimmäistä kutsutaan triangulaatioksi ja toinen on Gauss -determinanttien menetelmä.

Voi palvella sinua: olemassaolo ja ainutlaatuisuus lause: esittely, esimerkit ja harjoitukset

Triangulaatio

Se koostuu kuvan jakamisesta kolmioihin, joiden pinta -ala on helpompi laskea tai voidaan testata myös muiden lukujen kanssa, joiden pinta -ala on tiedossa, kuten neliöt, suorakulmiot ja trapetsidit.

Gauss -determinantit

Toinen tapa löytää epäsäännöllinen Pentagonin alue tai muu epäsäännöllinen monikulmio on kuvan asettaminen Cartesian koordinaattijärjestelmään, jotta voidaan löytää kärkipisteiden koordinaatit.

Tunnet nämä koordinaatit, Gauss -determinanttien menetelmää käytetään alueen laskemiseen, joka annetaan seuraavalla kaavalla:

Missä A on monikulmion alue ja (x_n , ja_n ) ovat kärkipisteiden koordinaatit. N -sivujen monikulmiossa on 5 kärkeä, Pentagonille se olisi n = 5:

Kaavan mukana olevat palkit ovat moduuliarvoja tai absoluuttista arvoa.

Tämä tarkoittaa, että vaikka operaation tulos on negatiivinen, meidän on ilmaista se positiivisella merkiksi, ja jos se on jo positiivinen, se on jätettävä kyseisen merkin mukana. Tämä johtuu siitä, että alue on aina positiivinen määrä.

Menettelyä kutsutaan Gauss -determinantteiksi sen luoja, saksalainen matemaatikko Carl F. Gauss (1777-1855). Osoitetut toiminnot vastaavat 2 x 2 -matriisin määrittäjää, esimerkiksi ensimmäinen determinantti on:

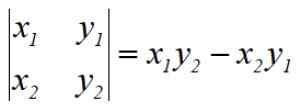
Pentagonin alueen löytämiseksi meidän on ratkaistava 5 determinanttitapaa, lisää tulos algebrallisesti, jaa se 2: lla ja ilmaista alueen aina aina positiivisella merkinnällä.

Ratkaisut

Harjoitus 1

Löydä tavallinen Pentagonin alue, jonka apoteemi on 4 cm: n arvoinen ja jonka puolella on 5.9 cm.

Ratkaisu

Koska se on tavallinen Pentagon, ja meillä on sivu- ja apoteemin mitta, käytämme aiemmin vähennettyä kaavaa:

Voi palvella sinua: Scaleno -kolmio

A = p x l_-Lla /2

Kehä P on yhtä suuri kuin 5A = 5 x 5.9 cm = 29.5 cm.

A = 29.5 cm x 4 cm / 2 = 59 cm²

Harjoitus 2

Etsi esitetty epäsäännöllinen pentagonin alue. Seuraavat mitat tunnetaan:

DC ≈

AE = AB = 5

BC = 12

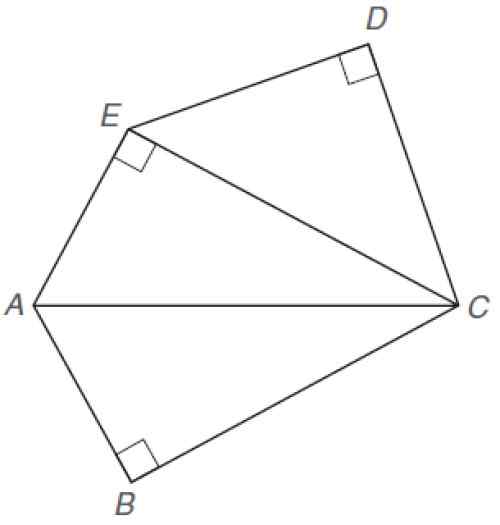Epäsäännöllinen pentagon. Lähde: Alexander, D. 2013. Geometria. Viides. Painos. Cengage -oppiminen.

Ratkaisu

Pentagonin alue on kolmioiden alueiden summa, jotka ovat suorakulmioita. Lausunnossa sanotaan, että DC ≈, siksi, kun sovelletaan Pythagoras -lause EDC -kolmioon, sillä on:

EY² = 2 Ed². Sitten EC = √2.Ed.

AEC: n ja ABC

Ea² + EY² = AB² + BC²

Kuten EA ja AB mittaavat saman, saadaan, että:

EC = BC = √2.Ed

Koska BC = 12, sitten ED = 12 / √2 = 8.485.

Näillä arvoilla lasketaan kunkin kolmion pinta -ala ja lisäämme ne lopussa.

EDC -kolmioalue 

Ed X DC /2 = 8.485² / 2 = 36

AEC -kolmion alue 

EA X EC / 2 = EA X √2.ED / 2 = 5 x √2. 8.485/2 = 30

ABC -kolmion alue 

AB X BC / 2

Sitten etsitty alue on:

5 x 12/2 = 30

Se on sama kuin kolmion AEC, koska molemmilla on samat toimenpiteet.

Epäsäännöllinen Pentagonin alue

Lopuksi pyydetty alue on kolmen kolmion alueiden summa:

A = 36 + 30 + 30 yksikköä = 96 yksikköä.

Viitteet

1. Alexander, D. 2013. Geometria. Viides. Painos. Cengage -oppiminen.
2. Matematiikan avoin viite. Monikulmioalue. Toipunut: MathPenref.com.
3. Maailmankaikkeuden kaavat. Epäsäännöllisen pentagonin alue. Toipunut: UniversOformulat.com.
4. Maailmankaikkeuden kaavat. Tavallisen Pentagonin alue. Toipunut: UniversOformulat.com.
5. Wikipedia. Pentagon. Palautettu: on.Wikipedia.com.