Fyysinen

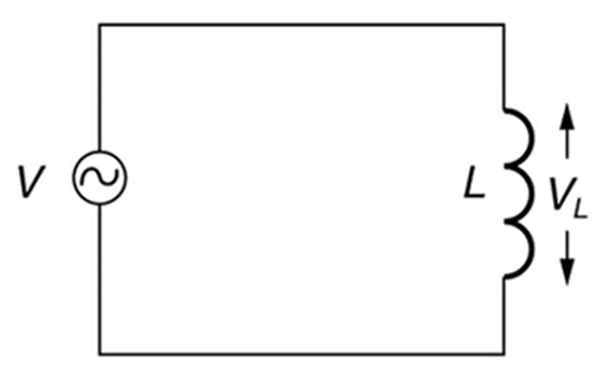
Induktiivinen reaktanssi

Induktiivinen reaktanssi
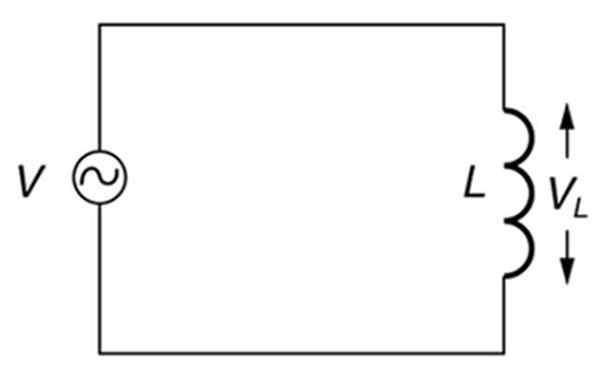Puhtaasti induktiivinen vaihtoehtoinen piiri. Lähde: Avaa stax. Korkeakoulufysiikka.

Mikä on induktiivinen reaktanssi?

Se Induktiivinen reaktanssi Se viittaa kelan esittämään vastustukseen virran kulkemiseen vaihtoehtoisessa piirissä. Toisin sanoen, indusoijan kyky vähentää virtaa vaihtoehtoisessa piirissä. Merkitty nimellä xLens, Sen arvo riippuu jännitteen induktanssista ja kulmataajuudesta:

XLens= Ω ∙ L

Missä ω on radiaanien/s ja l induktanssin kulmataajuus, mitattuna Henrios (H): ssä kansainvälisessä yksikköjärjestelmässä, jos.

Suuret induktanssit tuottavat suurta induktiivista reaktiivisuutta, koska niiden muutosvastus on suurempi. Ja reaktanssi kasvaa myös taajuuden kanssa, joten tietty induktanssi L tuottaa suuremman reaktanssin, mitä suurempi jännitetaajuus.

Induktiivinen reaktanssiyksikkö on ohmio, jonka symboloi ω. Se on sama sähkövastuksen yksikkö, mutta toisin kuin tämä, xLens Se ei ole vakio, koska se riippuu käytetyn vaihtoehtoisen jännitteen taajuudesta.

Siksi piirissä, jonka ainoat elementit ovat vaihtoehtoinen lähde ja induktanssi (induktiivinen piiri), kuten yllä esitetty kuva, induktiivinen reaktanssi riippuu lähteen taajuudesta.

X: n analogia kuitenkinLens Sähkökestävyydellä se voidaan laajentaa induktiiviseen piiriin, mikä mahdollistaa Ohmin lain soveltamisen. Jos x on määriteltyLens jänniteamplitudien välisenä suhteessa VLens Induktorissa ja nykyisessä ILens Se ylittää sen:

XLens = VLens / YoLens

Voit kirjoittaa ohmin lain puhtaasti induktiivisille piireille seuraavasti:

VLens = XLens∙ ILens

Induktiiviset reaktanssikaavat

Induktiivisen reaktanssin laskemiseksi käytetään alussa annettua kaavaa, jossa L edustaa induktanssia (Henrios) ja ω on kulmataajuus (radiaanit/sekunti):

Voi palvella sinua: Millikan -kokeilu: Menettely, selitys, merkitys

XLens= Ω ∙ L

On yleistä, että taajuus ilmaistaan ​​Hertz tai Hertziossa (Hz). Tässä tapauksessa se merkitsee F ja liittyy kaavan kautta kulmataajuuteen:

Ω = 2π ∙ f

Tässä tapauksessa reaktanssi lasketaan seuraavasti:

XLens= 2πf ∙ l

Missä tahansa näistä kaavoista induktiivinen reaktanssi johtaa ohmeihin, kuten aiemmin selitettiin.

Induktanssin vaikutus induktiiviseen piiriin

Koska induktanssi vastustaa virran muutoksia tai variaatioita, induktiiviselle reaktanssille on ominaista virran aallon viivästyminen jänniteaallon suhteen.

Seuraavassa kaaviossa, joka näyttää jännitteen VLens (Sininen) ja nykyinen ILens (punainen) induktorissa, molemmat sinoidisesti, havaitaan, että molemmat aallot ovat vanhentuneita 90º. Alkaen t = 0, jännitearvo on enimmäismäärä, mutta virta on nolla tuolloin.

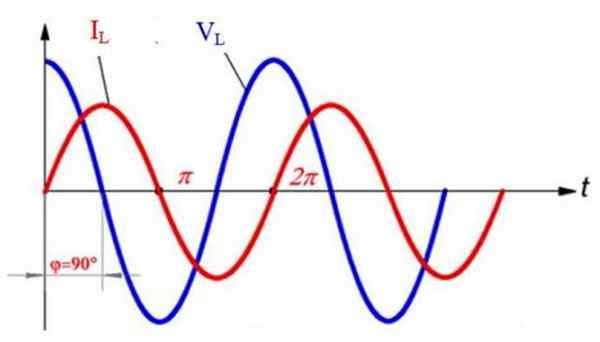Vaihtoehtoinen virta ja jännite induktiivisessa piirissä. Valmistaja: f. Zapata.

Myöhemmin havaitaan, että virta saavuttaa maksimiarvonsa t = π /2, mutta siihen mennessä jännite peruutetaan ja sijoittaa sen napaisuuden, ts. Se tulee negatiiviseksi. Samanaikaisesti virta vähentää sen arvoa, kun taas jännite muuttuu yhä negatiivisemmaksi.

Myöhemmin, kun T = π, jännite saavuttaa suurimman suuruuden, vaikka käänteisen napaisuuden ja sitten virta peruutetaan. Kaikesta tästä seuraa, että aina kun VLens Se saavuttaa huipun, virta peruutetaan, ja joka kerta kun virta saavuttaa suurimman suuruuden, jännite on 0.

Virta saavuttaa huipunsa aina jännitteen jälkeen, ja tämä johtuu siitä, että kuten alussa todettiin, induktanssi vastustaa tai vähenee.

Voi palvella sinua: Mekaaninen etu: Kaava, yhtälöt, laskenta ja esimerkit

Kuinka laskea induktiivinen reaktanssi

Induktiivinen reaktanssin laskeminen on hyvin yksinkertaista: on tarpeen tietää induktanssin arvo ja käytetyn vaihtoehtoisen jännitteen taajuus. Sitten nämä tiedot korvataan yhdessä edellisessä osassa annetuista kaavoista ja vastaava toiminta suoritetaan.

Seuraavat esimerkit ja ratkaisut harjoitukset osoittavat, kuinka se tehdään eri tilanteissa.

Esimerkit

Esimerkki 1

Oletetaan, että L = 5 mh: n induktori, johon käytetään vaihtoehtoista taajuusjännitettä 60.0 Hz. Induktiivinen reaktanssi tässä tapauksessa lasketaan:

XLens= 2πf ∙ l

Mutta ennen arvojen korvaamista induktanssista tulee tulla Henrios, kertomalla 1 × 10 -kerroksella−3. Siksi:

L = 5 × 10−3 H

Niin:

XLens= 2πf ∙ l = xLens= 2π × 60 Hz × 5 × 10−3 H = 1. 88 ohmia

Esimerkki 2

Nyt sama induktanssi on kytketty toiseen vaihtoehtoiseen taajuusjännitteeseen: 10.0 kHz. Tässä tapauksessa induktanssi on suurempi reaktanssi:

XLens= 2πf ∙ l = xLens= 2π × 10.0 × 103 Hz × 5 × 10−3 H = 314.2 ohmia

Esimerkki 3

Esimerkkien 1 ja 2 induktanssiin käytetyn jännitteen arvo on 120 V RMS. Vastaava RMS -virta määritetään ohmin V -lain kauttaLens = XLens∙ ILens-

YllyttääLens = VLens / XLens

Taajuudelle 60.0 Hz, virta on:

YllyttääLens = 120 V / 1. 88 ohm = 63.8 a

Ja taajuudelle 10.0 kHz:

YllyttääLens = 120 V / 314.2 ohmia = 0.38 a

Koska jälkimmäisessä tapauksessa reaktanssi on paljon suurempi, virran odotetaan olevan pienempi. Tämä ominaisuus tekee induktorista korkeataajuussuodattimen, ominaisuus, jota käytetään äänilaitteiden korkeataajuusäänien vähentämiseen tai laitteiden suojaamiseen äkillisiltä nykyisiltä UPS: ltä, muun muassa.

Voi palvella sinua: Steiner Lause: Selitys, sovellukset, harjoitukset

Ratkaisut

Harjoitus 1

Määritä induktiivinen reaktanssi piirissä, joka koostuu 2: n induktanssista.5 mh, sarjassa, jossa on vaihtoehtoinen jännitelähde, jonka taajuus on 75 R.p.m.

Ratkaisu

Täydellinen vallankumous tai sykli on yhtä suuri kuin 2π radians, ja minuutissa on 60 sekuntia, joten taajuus on 75 r.p.M vastaa:

75 r.p.M = 75 × 2π radians / 60 sekuntia = 7.85 radiaania/s

Ja tällä arvolla reaktanssi on:

XLens= Ω ∙ L = (7.85 radiaania/s) × 2.5 × 10−3 H = 0.02 Ω

Harjoitus 2

Sarjainduktanssia käytetään tietokoneen lähteen kanssa korkeiden taajuuksien kohinan suodattamiseksi.

a) Mikä tulisi olla vähimmäisinduktanssiarvo, joka on tarpeen 2 kΩ: n reaktanssin tuottamiseksi, jos suodattavan signaalin taajuus on 15 kHz?

b) Löydä tämän induktorin reaktanssi 60 Hz: n taajuudella.

Liittää jhk

XLens = 2 kΩ = 2000 Ω

F = 15 kHz = 15000 Hz

Siksi yhtälön x puhdistaminenLens= 2πf ∙ l, sinulla on:

L = xLens / 2π ∙ F = 2000 ω / 2π × 15000 Hz = 0.0212 H = 21.2 mh

Ratkaisu b

Käyttämällä x uudelleenLens= 2πf ∙ L, mutta f = 60 Hz: lla, tulokset:

XLens= 2π × 60 Hz × 0.0212 h = 8 ohmia.

Viitteet

  1. Bauer, W. (2011). Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill. 
  2. Giancoli, D. (2006). Fysiikka: sovellusten periaatteet. Kuudes. Ed Prentice Hall.
  3.  Katz, D. (2013). Fysiikka tutkijoille ja insinööreille. Perusteet ja yhteydet. Cengage -oppiminen.
  4. Avaa stax. Korkeakoulufysiikka. Haettu osoitteesta: OpenStax.org.
  5. Sears, z. (2016). Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Nide 2. Pearson