Bravais Networks -konsepti, ominaisuudet, esimerkit, harjoitukset

Se Bravais -verkot Ne ovat sarja neljätoista kolmen dimensionaalista yksikkösolua, joissa kideen atomit. Nämä solut koostuvat kolmiulotteisesta pisteistä, jotka muodostavat perusrakenteen, joka toistetaan määräajoin kolmessa alueellisessa suunnassa.

Tämän määrityksen alkuperän peruskaiteisiin rakenteisiin tulee vuodesta 1850, jolloin Auguste Bravais osoitti, että mahdollinen on vain 14 mahdollista kolmen dimensionaalista yksikkösolua.

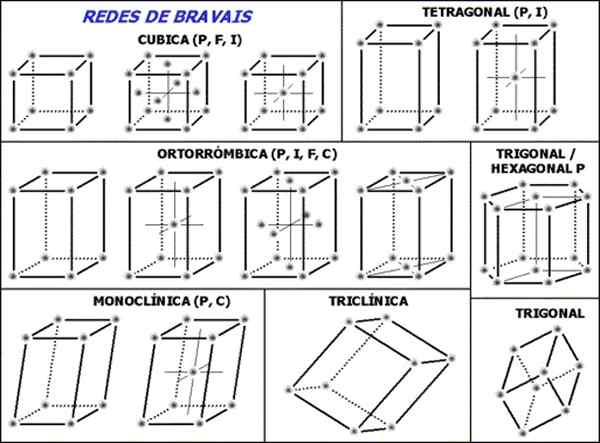
Kuvio 1. Bravais -verkot ovat 14 välttämätöntä ja tarpeeksi yksikkösolua kaikkien kiteisten rakenteiden kuvaamiseksi. (Wikimedia Commons)

14 Bravais -verkkojen joukko on jaettu seitsemään ryhmään tai rakenteisiin solujen geometrian mukaan, nämä seitsemän ryhmää ovat:

1- kuutio

2- tetragonaalinen

3- Ortorrominen

4- Trigonal-heksagonaali

5- monokliininen

6- trikliininen

7- Trigonaalinen

Jokainen näistä rakenteista määrittelee yhtenäisen solun, tämä on pienin osa, joka säilyttää lasin atomien geometrisen järjestelyn.

[TOC]

Bravais -verkkojen ominaisuudet

Bravaisin neljätoista verkkoa, kuten edellä todettiin, on jaettu seitsemään ryhmään. Mutta jokaisella näistä ryhmistä on yksikkösolut ominaisparametreilla, jotka ovat:

1- Verkkoparametri (a, b, c)

2- Atomien lukumäärä solua kohti

3- Verkkoparametrin ja atomiradion välinen suhde

4- Koordinointinumero

5- Pakkauskerroin

6- interstitiaaliset tilat

7- Vektoreiden a-, b-, c-käännöksillä kiteinen rakenne toistetaan.

Kuutioverkot

Se koostuu yksinkertaisesta tai kuutiomestarisesta verkosta, kuutioverkosta, joka on keskittynyt kasvoihin tai kuutioverkkoon F ja kuutioverkko, joka on keskittynyt kuutiorunkoon tai verkkoon.

Kaikissa kuutioverkoissa on kolme Verkkoparametrit Vastaa x, y -osoitteita, z sama arvo:

A = b = c

Kuutioverkko P

On kätevää korostaa, että atomit edustavat palloja, joiden keskukset ovat kuutiosolun pikulmioissa.

Voi palvella sinua: keinotekoiset satelliitit

Kuutioverkon tapauksessa P Atomien lukumäärä solua kohti Se on 1, koska jokaisessa kärjessä vain atomin kahdeksas osa on yksikkösolun sisällä, sitten 8*⅛ = 1.

Hän Koordinointinumero Osoittaa atomien lukumäärän, jotka ovat lähellä olevia naapureita kiteisessä verkossa. Kuutioverkon P: n tapauksessa koordinointinumero on 6.

Kuutioverkko I

Tämän tyyppisessä verkossa kuution kärkipisteiden atomien lisäksi kuution keskellä on atomi. Niin atomin luku solua kohti Yhtenäinen kuutioverkossa P on 2 atomia.

Kuva 2. Kehonkeskeinen kuutioverkko.

Kuutioverkko f

Se on kuutioverkko, että kärjessä olevien atomien lisäksi on atomi kunkin kuution pinnan keskellä. Hän Atomien lukumäärä solua kohti Se on 4, koska jokaisella kuudesta kasvojen atomista on puolet solun sisällä on 6*½ = 3 plus 8*⅛ = 1 kärjessä.

Kuva 3. Kuutioverkko, joka on keskittynyt kasvoihin.

Kuusikulmainen verkko

Tässä tapauksessa yksikkösolu on suora kuusikulmainen prisma. Kuusikulmainen verkolla on kolme Verkkoparametrit vastaava seuraavan suhteen täyttäminen:

A = b ≠ c

On kulma vektorin A ja B välillä 120º, kuten kuvassa esitetään. Kun taas vektorien A ja C välillä sekä B: n ja C: n välillä ovat suorat kulmat.

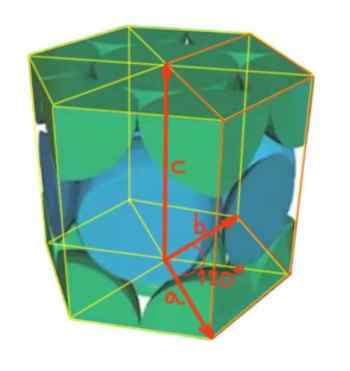Kuva 4. Kuusikulmainen verkko.

Hän Atomien lukumäärä solua kohti Se lasketaan seuraavasti:

- Jokaisessa kuusikulmaisen prisman 2 emäksessä on 6 atomia kuudessa kärkipisteessä. Jokainen näistä atomeista on ⅙ yhtenäistä solua.

- Kunkin kahden kuusikulmaisen emäksen keskellä on yksi atomi, joka vie 1/2 yhtenäistä solua.

- Kuuksikulmaisen prisman kuuden sivupinnan kohdalla on 3 atomia, joista kukin vie yksikkökennon ⅔, ja 3 atomia, jotka miehittävät jokaisen yksikön solun tilavuuden ⅓.

Se voi palvella sinua: Kuule voima: pinta- ja massavoimat

(6 x ⅙) x 2 + ½ x 2 + ⅔ x 3 + ⅓ x 3 = 6 

Verkkoparametrien A ja B välinen suhde atomisäteen R kanssa olettaen, että kaikki atomit ovat yhtä radioita ja ovat kosketuksissa: ovat: 

a/r = b/r = 2

Esimerkit

Metallit ovat tärkeimpiä esimerkkejä kiteisistä rakenteista ja myös yksinkertaisimpia, koska ne koostuvat yleensä yhden tyyppisestä atomista. Mutta on myös muita ei -metallisia yhdisteitä, jotka muodostavat myös kiteisiä rakenteita, kuten timantti, kvartsi ja monet muut.

- Rauta

Raudassa on yksinkertainen kuutioyksikkökenno, jossa on verkkoparametri tai reuna A = 0,297 nm. 1 mm: ssä on 3,48 x 10^6 yksikkösoluja.

- Kupari

Siinä on kuutiometriä kiteinen rakenne, joka on keskittynyt kasvoihin, jotka on muodostettu vain kupariatomeilla.

- Jalokiviä

Arvokkaat jalokivet ovat kiteisiä rakenteita pohjimmiltaan sama yhdiste, mutta pienillä epäpuhtauksien osalla, jotka ovat usein vastuussa niiden väristä.

Timantti

Se koostuu vain hiilestä eikä sisällä epäpuhtauksia, minkä vuoksi siitä puuttuu väri. Timantilla on Kuutiomainen rakenne (isometrinen hexoctahedral) ja on vaikeimmin tunnettu materiaali.

Kvartsi

Se koostuu piidioksidista, se on yleensä väritön tai valkoinen. Sen kiteinen rakenne on trigonaalinen-trapezoédrica.

Rubiini 

Se koostuu alumiinioksidista, jolla on kromien epäpuhtauksia, jotka antavat sille ominaisen punaisen värin. Muodostaa yhden Kuusikulmainen kiteinen verkko.

Safiiri 

Se on myös alumiinioksidikide, mutta titaanin ja raudan epäpuhtauksilla, jotka ovat vastuussa niiden sinisestä väristä erilaisissa sävyissä. Kuten rubiinilla kuusikulmainen rakenne.

Jade

Arvokas kivi yleensä vihreä, on Monokliininen rakenne Ja se koostuu rauta-magnesium-calcio-silikaatista.

Topaasi 

Se on väritön a Ortorrominen rakenne alumiini-hydroksidisilikaattifluoridi.

Ratkaisut

Harjoitus 1

Löydä verkkoparametrin ja kuutioverkon atomin säteen välinen suhde F.

Se voi palvella sinua: Big Bang -teoria: Ominaisuudet, vaiheet, todisteet, ongelmat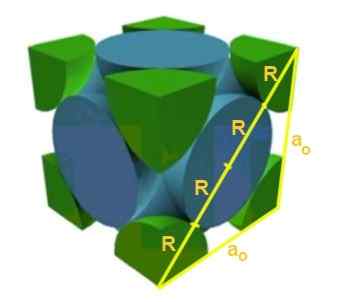

Ratkaisu: Ensinnäkin oletetaan, että atomit on esitetty palloina kaikki säde r "kosketuksessa" toisiinsa, kuten kuvassa on esitetty. Suorakulmio kolmio on muodostettu, jossa on täytettävä, että:

(4 r)^2 = a^2 + a^2 = 2 a^2

Joten sinulla on, että Edge-Radio-suhde on:

A/r = 4/√2

Harjoitus 2

Löydä verkon parametrin ja atomissäteen välinen suhde kuutioverkkoon I (Body Centered).

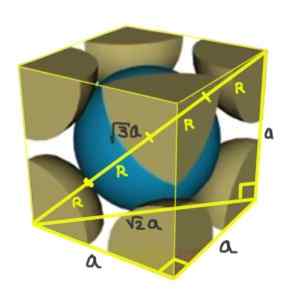
Ratkaisu: Atomien oletetaan edustettavana kaikina sädepaikoina "kosketuksessa" toisiinsa, kuten kuvassa esitetään.

Kaksi suorakulmiota muodostetaan yksi hypotenusa √2a: sta ja toisesta hypotenusista √3a, joka voidaan osoittaa käyttämällä Pythagoran lausetta. Sieltä sinun on suhde verkkoparametrin ja kuutioverkon I atomisäteen välillä (kehossa keskitetty) on:

A/r = 4/√3

Harjoitus 3

Löydä pakkauskerroin F kuutiorakenteen F yksikkösolusta (kuutio keskittynyt kasvoihin), joissa atomeilla on radio r ja ne ovat "kosketuksessa".

Ratkaisu: Pakkauskerroin F määritetään suhteeksi yksikkösolun atomien ja solun tilavuuden välillä: solun tilavuuden välillä:

F = vatomit / Vsolu

Kuten edellä on osoitettu, atomien lukumäärä kasvoihin keskittyneen kuutioverkon yksikkökenno on 4, joten pakkauskerroin on:

F = 4 [4πr^3/3] /[a^3] =…

… 4 [4πr^3/3]/[4r/√2]^3 = (√2) π/6 = 0,74

Viitteet

1. Kristallirakenteet akateeminen resurssikeskus. [PDF]. Haettu 24. toukokuuta 2018: Verkko.iit.Edu
2. Kiteet. Haettu 26. toukokuuta 2018, osoitteesta: Adthco.com
3. Lehdistökirjat. 10.6 Latice -rakennetta kiteisissä kiinteissä aineissa. Haettu 26. toukokuuta 2018, osoitteesta: OpenTextbc.Ac
4. Ming. (30. kesäkuuta 2015). Tyyppikristallirakenteet. Haettu 26. toukokuuta 2018, osoitteesta: Crystalvisions-Film.com
5. Helmestine, Anne Marie, PH.D -d. (31. tammikuuta 2018). Tyyppisiä 
6. Kittel Charles (2013) Solid State Fysiikka, tiivistetty ainefysiikka (8. painos). Viiva.
7. Khi. (2007). Kiteiset rakenteet. Haettu 26. toukokuuta 2018, Folk.Ntnu.Ei
8. Wikipedia. Bravais Latices. Haettu: vuonna.Wikipedia.com.