Kupera polygonin määritelmä, elementit, ominaisuudet, esimerkit

Eräs kuperan monikulmio Se on geometrinen hahmo, joka sisältyy karakterisoituun tasoon, koska siinä on kaikki diagonaalit ja sen kulmat mittaavat alle 180º. Sen ominaisuuksien joukossa ovat seuraavat:

1) Se koostuu n peräkkäisistä segmenteistä, joissa viimeinen segmentti liittyy ensimmäiseen. 2) Mikään segmentistä ei ole ristetty siten, että se rajaa tasoa sisätiloissa ja toinen ulkopinta. 3) Jokainen sisäalueen kulmasta on tiukasti alhaisempi kuin tasainen kulma.

Kuvio 1. Polygonit 1, 2 ja 6 ovat kupera. (Valmistaja Ricardo Pérez).

Yksinkertainen tapa määrittää, onko monikulmio kupera vai ei ole harkita yhden sivun läpi kulkevaa linjaa, joka määrittää kaksi puolipolunia. Jos jokaisella toisaalta kulkevalla rivillä, monikulmion toiset puolet ovat samassa puolipisteessä, se on sitten kupera monikulmio.

[TOC]

Monikulmion elementit

Jokainen monikulmio koostuu seuraavista elementeistä:

- Puolet

- Kärjet

Sivut ovat kumpikin peräkkäisiä segmenttejä, jotka muodostavat monikulmion. Monikulmiossa mikään segmentistä, jotka tekevät siitä.

Verkit ovat kahden peräkkäisen segmentin ammattiliittopisteet. Monikulmiossa kärkipisteiden lukumäärä on aina yhtä suuri kuin sivujen lukumäärä.

Jos monikulmion ristin kaksi puolta tai segmenttiä, sinulla on ristin monikulmio. Risteyspistettä ei pidetä kärkipisteenä. Ristipolygon on ei-kupera monikulmio. Kaatuneet monikulmiot ovat ristissä monikulmioita, joten ne eivät ole kupera.

Se voi palvella sinua: analyyttinen geometria

Kun monikulmiossa on kaikki saman pituiset sivut, siellä on sitten tavallinen monikulmio. Kaikki tavalliset monikulmiot ovat kuperoja. 

Kupera ja ei-kupera monikulmio

Kuvio 1 esittää useita monikulmioita, jotkut niistä ovat kuperoja ja toiset eivät. Analysoidaan heidät:

Numero 1 on kolmipuolinen monikulmio (kolmio) ja kaikki sisäkulmat ovat alle 180º, joten se on kupera monikulmio. Kaikki kolmiot ovat kuperat monikulmiot.

Numero 2 on neljän puolen monikulmion (nelikulmainen), jossa ketään sivuista ei ole sieppattu ja myös jokainen sisäkulmasta on alle 180º. Se on silloin neljä -puolinen kupera monikulmio (kupera kvadrilateraalinen).

Toisaalta numero 3 on neljän puolen monikulmio, mutta yksi sen sisäkulmista on suurempi kuin 180º, joten se ei täytä kupera -olosuhteita. Toisin sanoen se on ei-kupera-sivuinen monikulmio, jota kutsutaan koveraksi kvadrilateraaliseksi.

Numero 4 on neljänsegmentin (sivut) monikulmio, joista kaksi sieppataan. Neljä sisäkulmaa ovat alle 180º, mutta kun molemmat puolet ylittävät, ne ovat ei-kuivia ristipohja (risti-nelikulmainen).

Toinen tapaus on numero 5. Tämä on viisipuolinen monikulmio, mutta koska yksi sen sisäkulmista on suurempi kuin 180º, silloin on kovera monikulmio.

Lopuksi, numerolla 6, jolla on myös viisi puolta, on kaikki sen sisäkulmat alle 180º, joten se on viisipuolinen kupera monikulmio (kupera pentagon).

Voi palvella sinua: näytteenottovirhe: kaavat ja yhtälöt, laskenta, esimerkit

Kupera monikulmioominaisuudet

1- murrettu monikulmio tai yksinkertainen monikulmio jakaa sen sisältävän tason kahteen alueeseen. Sisustusalue ja ulkoinen alue, joka on monikulmio kahden alueen välinen raja.

Mutta jos monikulmio on lisäksi kupera, niin on olemassa yksinkertaisesti sukulainen sisäalue, mikä tarkoittaa, että minkä tahansa sisäalueen kahden pisteen ottaminen, se voi aina yhdistää kokonaisuudessaan oleva segmentti sisäalueelle.

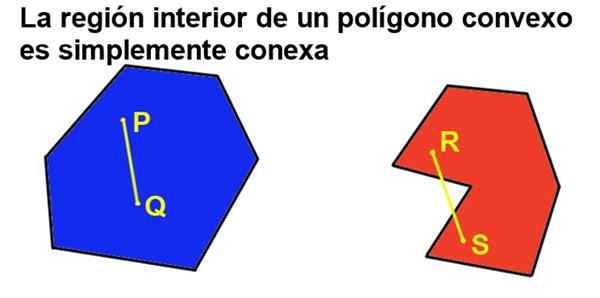Kuva 2. Kukkas monikulmio on yksinkertaisesti sukulainen, kun taas kovera ei ole. (Valmistaja Ricardo Pérez).

2- KAIKKI KUVAN POLOGONIN SÄÄKUMA ON PITKÄT TILINEN KULMA (180º).

3- Kaikki kuperan monikulmion sisäpisteet kuuluvat aina yhteen puoliksi määriteltyyn linjaan, joka kulkee kahden peräkkäisen kärjen läpi.

4- Kukkassa monikulmiossa kaikki diagonaalit sisältävät kokonaan sisäpohjaisen monikulmion alueella.

5- Kumperan monikulmion sisäpisteet kuuluvat kokonaisuudessaan kuperaan kulma-sektoriin, joka on määritelty jokaisella sisäkulmalla.

6- Jokainen monikulmio, jossa kaikki sen kärkipisteet ovat kehällä, on kupera monikulmio, jota kutsutaan sykliseksi monikulmioksi.

7- Jokainen syklinen monikulmio on kupera, mutta jokainen kupera monikulmio ei ole syklinen.

8- Jokainen murtamaton monikulmio (yksinkertainen monikulmio), jolla on kaikki sen tasa-arvoiset sivut, on kupera ja tunnetaan tavallisena monikulmion nimellä.

Diagonaalit ja kulmat kuperissa monikulmioissa

9- N-sivujen kuperan monikulmion diagonaalien kokonaismäärä annetaan seuraavalla kaavalla:

Se voi palvella sinua: Polybal -grafiikka

N = ½ n (n - 3)

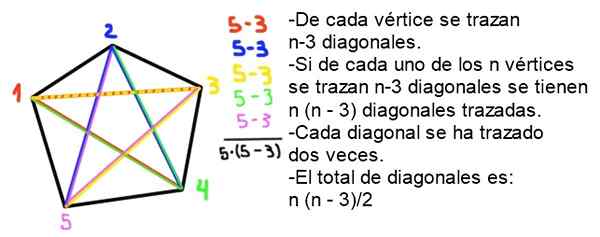
Esittely: Kunkin kärkipisteen n -sivujen kuperassa monikulmiossa piirretään, koska itse kärki ja kaksi viereistä sivua suljetaan pois. Koska siellä on n kärkiä, niitä piirretään yhteensä n - 2) diagonaaleja, mutta jokainen diagonaali piirrettiin kahdesti, joten diagonaalien lukumäärä (ilman toistoa) on N (n -2)/2.

10- N-puolien kuperan monikulmion sisäkulmien summa annetaan seuraavalla suhteella:

S = (n - 2) 180º

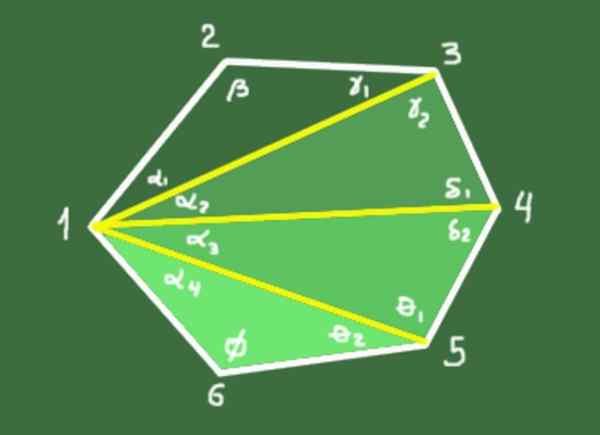
Esittely: N-3-diagonaalit vedetään kärkipisteestä, joka määrittelee N-2-kolmion. Kunkin kolmion sisäkulmien summa on 180º. N-2-kolmiokulmien kokonaismäärä on (N-2)*180º, joka vastaa monikulmion sisäkulmien summaa.

Esimerkit

Esimerkki 1

Syklinen kuusikulmio, se on kuusipuolinen monikulmio ja kuusi kärkipistettä, mutta kaikki kärkipisteet ovat samassa kehässä. Kaikki syklinen monikulmio on kupera.

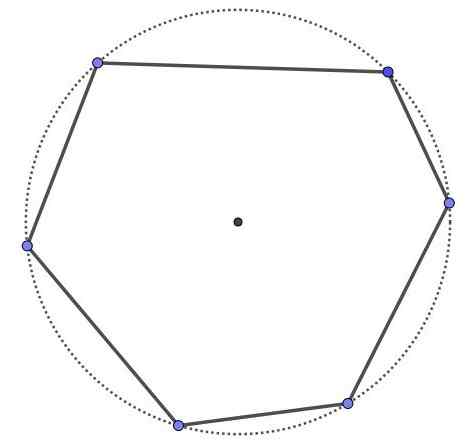Syklinen kuusikulmio.

Esimerkki 2

Määritä tavallisen engonin sisäkulmien arvo.

Ratkaisu: Engon on 9 -puolinen monikulmio, mutta se säätelee myös kaikkia sivujaan ja kulmia ovat samat.

Kaikista 9 -puolison monikulmion sisäkulmien summa on:

S = (9 - 2) 180º = 7 * 180º = 1260º 

Mutta on olemassa 9 sisäistä kulmaa, jotka ovat yhtä suuret α, joten seuraava tasa -arvo on täytettävä:

S = 9 α = 1260º

Mistä seuraa, että tavallisen engonin kunkin sisäisen kulman α -mitta on:

α = 1260º/9 = 140º