Oikeanpuoleinen sääntö

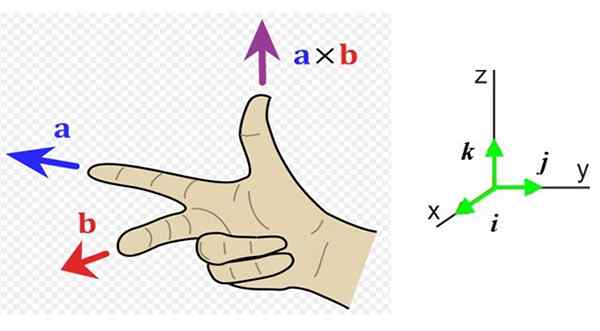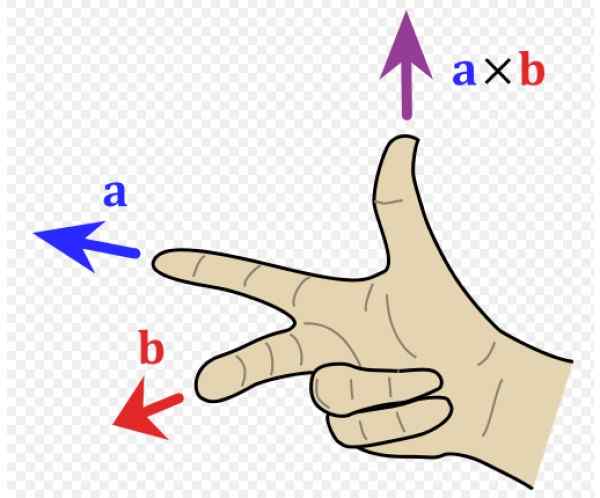
Kuvio 1. Oikeanpuoleinen sääntö. Lähde: Wikimedia Commons. ACDX [CC BY-S (http: // creativecommons.Org/lisenssit/by-SA/3.0/]].

Mikä on oikean käden sääntö?

Se oikeanpuoleinen sääntö Se on muistomerkitys vektorituotteesta tai ristituotteesta johtuvan vektorin suunnan ja suunnan määrittämiseksi. Sitä käytetään laajasti fysiikassa, koska vektorituotteen tulosta on tärkeitä vektorialueita. Näin on esimerkiksi vääntömomentti, magneettinen voima, kulmavirta ja magneettinen momentti.

Olla kaksi yleistä vektoria -lla ja b - Kenen ristituote on -lla x b -. Tällaisen vektorin moduuli on:

-lla x b = -lla.b -.synti α

Missä α on vähimmäiskulma -lla ja b -, Kun taas a ja b edustavat moduulejaan. Vektoreiden erottamiseksi moduuleistaan ​​käytetään rohkeita kirjaimia.

Nyt meidän on tiedettävä tämän vektorin suunta ja merkitys, joten on kätevää saada referenssijärjestelmä, jolla on tilaa kolme suuntaa (kuva 1 oikea). Yksikkövektorit Yllyttää, J - ja k -k - He osoittavat lukijalle (sivulta) oikealle ja ylöspäin.

Kuvan 1 jäljellä olevassa esimerkissä vektori -lla on menossa vasemmalle (osoite ja oikean käden negatiivinen ja etusormi) ja vektori b - menee lukijalle (osoite x oikean käden positiivinen, keskisormi).

Tuloksena oleva vektori -lla x b - on peukalon suunta ylöspäin z -z positiivinen.

Oikean käden toinen sääntö

Tätä sääntöä käytetään paljon, kun on suuria määriä, joiden suunta ja merkitys pyörivät, kuten magneettikenttä B - tuotettu ohuella ja suoraviivaisella johdolla, joka kuljettaa virtaa.

Tässä tapauksessa magneettikenttäviivat ovat samankeskisiä kehäjä johdin kanssa, ja käännöksen suunta saadaan tällä säännöllä seuraavasti: oikea peukalo osoittaa virran suunnan ja loput neljä sormea ​​ovat kaareva kentän suunta. Kuvaamme käsitettä kuvassa 2.

Voi palvella sinua: Joustavat iskut: ulottuvuudessa, erityistapauksissa, harjoituksissa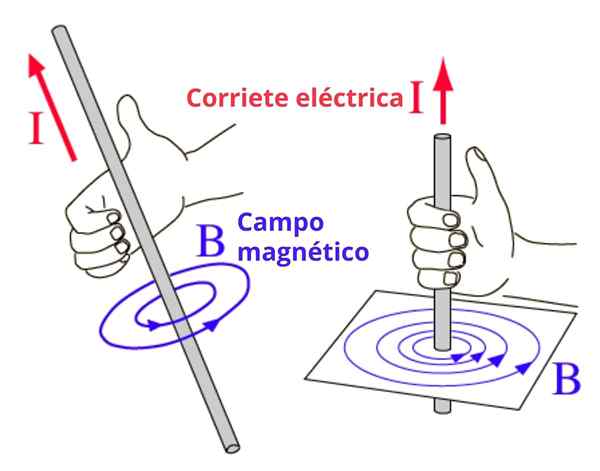Kuva 2. Oikeanpuoleinen sääntö magneettikentän verenkierron merkityksen määrittämiseksi

Oikean käden vaihtoehtoinen sääntö

Seuraava kuva näyttää oikeanpuoleisen säännön vaihtoehtoisen muodon. Valaistuessa esiintyvät vektorit ovat:

• Nopeus v täsmällisestä kuormasta.
• Magneettikenttä B - jonka sisällä kuorma liikkuu.
• F_{B -} Magneettikentän käyttämä voima kuormaan.

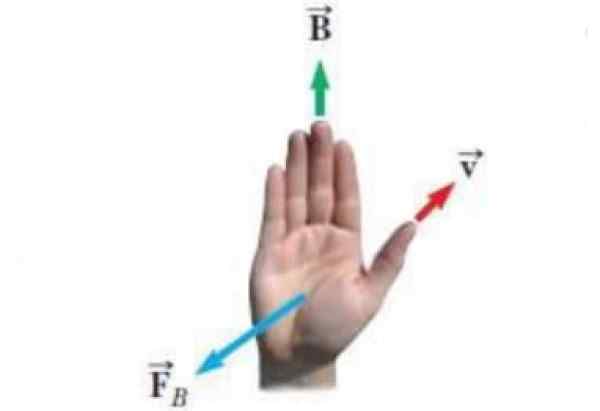Kuva 3. Oikean käden vaihtoehtoinen sääntö. Lähde: Wikimedia Commons. Asiantuntija [CC BY-SA (https: // creativecommons.Org/lisenssit/by-SA/4.0)]

Magneettisen voiman yhtälö on F_{B -} = qv x B - ja oikean käden sääntö tietää suunta ja tunne F_{B -} Se sovelletaan näin: V: n V: n mukaan jäljellä olevat neljä sormea ​​sijoitetaan kentän B mukaan. Niin F_{B -} Se on vektori, joka tulee kämmenestä, kohtisuorassa siihen, ikään kuin se työntäisi kuormaa.

Ota huomioon, että F_{B -} osoittaisi vastakkaiseen suuntaan, jos kuorma, joka olisi negatiivinen, koska vektorituote ei ole kommutatiivinen. Itse asiassa:

-lla x B = - b x -lla

Sovellukset

Oikeanpuoleista sääntöä voidaan soveltaa erilaisiin fyysisiin voimakkuuksiin, he katsotaan joihinkin:

Kulmanopeus ja kiihtyvyys

Molemmat kulmanopeus Ω Kuten kulmakiihtyvyys α He ovat vektoreita. Jos esine pyörii kiinteän akselin ympäri, se on mahdollista kulmanopeutta Ω.

Puolestaan ​​kulmakiihtyvyys α on sama osoite kuin Ω, Mutta sen merkitys riippuu siitä, onko Ω lisää tai vähentää sen suuruutta ajan myötä. Ensimmäisessä tapauksessa molemmilla on sama suunta ja merkitys, mutta toisessa heillä on vastakkaiset aistit.

Voi palvella sinua: Watt Law: Mikä on, esimerkkejä, sovelluksia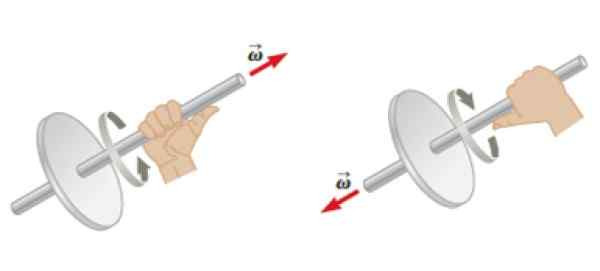Kuva 4. Kulmanopeuden suunnan ja suunnan määrittämiseksi sovellettu oikeanpuoleinen sääntö, joka on sovellettu kierto -objektiin. Lähde: Serway, R. Fyysinen.

Kulmainen vauhti

Kulmavektori Lens_JOMPIKUMPI hiukkasista, joka pyörii tietyn akselin ympäri tai määritellään sen välittömässä sijaintivektorin vektorituotena r -  ja lineaarisen liikkeen määrä p-

Lens = r - x p

Oikea -käsi -sääntöä sovelletaan tällä tavalla: etusormi asetetaan samaan suuntaan ja suuntaan r -, Keskisormi p, Sekä vaakasuorassa tasossa, kuten kuvassa. Peukalo ulottuu automaattisesti pystysuoraan ylöspäin osoittaen kulman vauhdin suunnan ja suunnan Lens_JOMPIKUMPI.

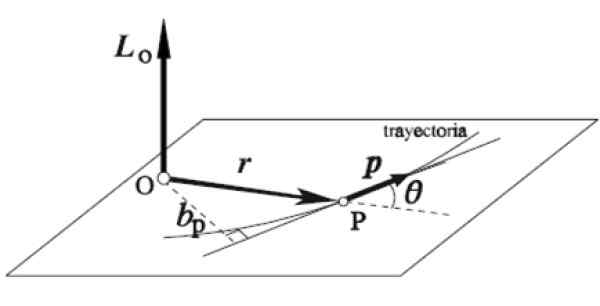Kuva 5. Kulmavektori. Lähde: Wikimedia Commons.

Harjoitukset

Harjoitus 1

Kuvion 6 kehrä menee nopeasti kulmanopeudella Ω ja sen symmetria -akseli rikkoutui hitaammin pystysuoran akselin ympärille z -z. Tätä liikettä kutsutaan prepressio. Kuvaile voimat, jotka vaikuttavat spiniin ja niiden tuottamiin vaikutuksiin.

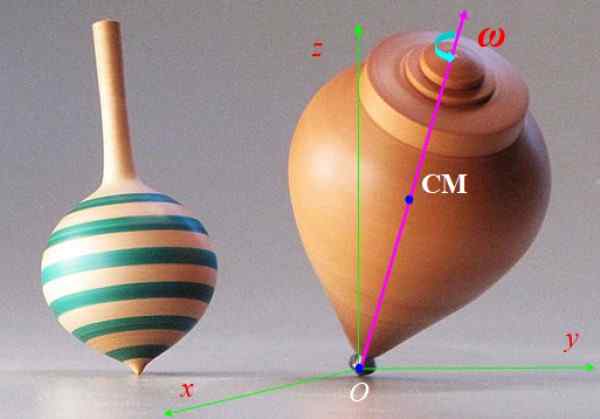Kuva 6. Kehruu. Lähde: Wikimedia Commons.

Ratkaisu

Spiniin vaikuttavat voimat ovat normaaleja N, levitetään tukipisteeseen maalla tai enemmän painoa mg, levitetään massa -cm: n keskelle, jossa on g Vakavuus kiihtyvyysvektori, suunnattu pystysuunnassa (katso kuva 7).

Molemmat voimat ovat tasapainossa, joten spin ei liiku. Paino kuitenkin tuottaa vääntömomentin tai vääntömomentin τ Net noin pisteestä tai, antanut:

τ_JOMPIKUMPI = r -_JOMPIKUMPI x F, kanssa F = Mg.

Kuten r - ja mg He ovat aina lentokoneessa, kun spin kääntyy, oikean käden säännön mukaan vääntömomentti τ_JOMPIKUMPI Se sijaitsee aina lentokoneessa Xy, kohtisuorassa molemmat a r - kuten g.

Ota huomioon, että N ei tuota vääntömomenttia O: lle, koska sen vektori r - Suhteessa tai on nolla. Tuo vääntömomentti aiheuttaa muutoksen kulmavirrassa, joka aiheuttaa spinin precession Z -akselin ympärillä.

Voi palvella sinua: Termodynaaminen tasapaino: Luokat ja sovellukset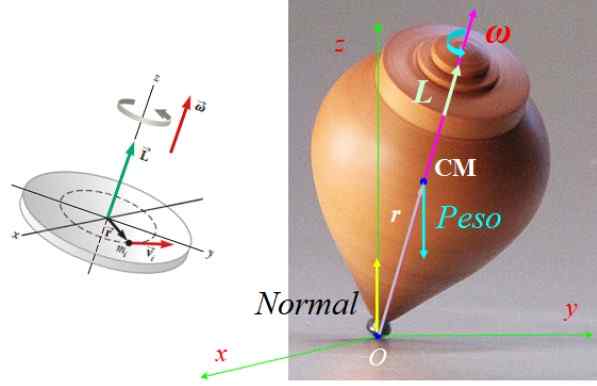Kuva 7. Spin ja sen kulmavirtavektori toimivia voimia. Vasemman kuvan lähde: Serway, R. Fysiikka tieteen ja tekniikan fysiikka.

Harjoitus 2

Osoita kulman momenttivektorin suunta ja suunta Lens kuvion 6 Trumpesta.

Ratkaisu

Kaikissa spin -pisteissä on massa m_Yllyttää, nopeus v_Yllyttää ja sijaintivektori r -_Yllyttää, Kun se kiertää Z -akselin ympäri. Kulmainen vauhti Lens_Yllyttää mainitun hiukkasen on:

Lens_Yllyttää = r -_Yllyttää x p_Yllyttää = r -_Yllyttää x m_Yllyttääv_Yllyttää

Kun otetaan huomioon r -_Yllyttää ja v_Yllyttää Ne ovat kohtisuorassa, Lens On:

Lens_Yllyttää = m_Yllyttäär -_Yllyttääv_Yllyttää

Lineaarinen nopeus v liittyy kulmanopeuteen Ω kautta:

v_Yllyttää = r_YllyttääΩ

Siksi:

Lens_Yllyttää = m_Yllyttäär -_Yllyttää (R_YllyttääΩ) = m_Yllyttäär -_Yllyttää²Ω

TROMPO L: n kokonainen kulmavirta on kunkin hiukkasen kulmanmomentin summa:

L = (∑m_Yllyttäär -_Yllyttää² ) Ω

∑ m_Yllyttäär -_Yllyttää²  Se on spinin hitaus I -hetki, sitten:

Lens= IΩ

Siksi Lens ja Ω Heillä on sama suunta ja merkitys, kuten kuvassa 7 esitetään.