Simpson Rule Formula, esittely, esimerkit, harjoitukset

Se Simpson -hallinto Se on menetelmä suunnilleen määriteltyjen integraalien laskemiseksi. Se perustuu integraatiovälin jakamiseen ala-intervalospariin, joka on tasapuolisesti etäisyydellä.

Kahden peräkkäisen alaluokan ääriarvot määrittelevät kolme pistettä, joka säätää parabolia, jonka yhtälö on toisen asteen polynomi. 

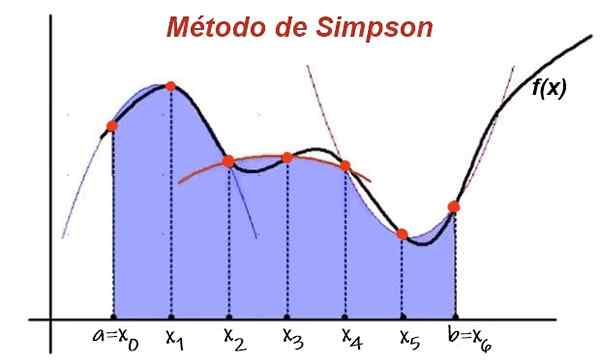
Kuvio 1. Simpson -menetelmässä integraatioväli on jaettu yhtä suuren leveyden väliajoihin. Funktiota lähentää vertausta jokaisessa kahdessa alakohdassa ja olennaiset lähestymistavat vertausten alla olevan alueen summan perusteella. Lähde: UPV.On.

Sitten funktion käyrän alla olevaa aluetta kahdessa peräkkäisessä väliajoin lähtee interpoloinnin polynomialueella. Lisäämällä panoksen kaikista peräkkäisistä alakohtaisista vertausalueesta, integraalin likimääräinen arvo.

Toisaalta, koska vertauksen integraali voidaan laskea algebrallisesti tarkalleen, niin on mahdollista löytää analyyttinen kaava määritellyn integraalin likimääräiselle arvolle. Tunnetaan nimellä Simpson -kaava.

Näin saadun likimääräisen tuloksen virhe pienenee siinä määrin, että alajakojen lukumäärä n on suurempi (ollessa n vääntömomentti).

Annetaan lausekkeen alapuolella, joka mahdollistaa lähestymisvirheen ylemmän tason arvioinnin integraaliin I, kun kokonaisvälin säännöllisten alaryhmien osio [a, b] on tehty [b].

[TOC]

Kaava

Integraatioväli [A, B] on jaettu N -subintervalsiin, jolloin n on vääntömomentti. Kunkin alajaon leveys on:

H = (b - a)/n

Tällä tavalla osio on tehty [a, b]: osio tehdään:

X0, x1, x2, ..., xn-1, xn

On x0 = a, x1 = x0 + h, x2 = x0 + 2h,…, xn-1 = x0 + (n-1) h, xn = x0 + nh = b.

Se voi palvella sinua: Ero ympyrän ja kehän välillä (esimerkkien kanssa)

Kaava, joka sallii suunnilleen määritellyn integraalin ja jatkuvan toiminnan laskemisen ja edullisesti pehmeän, aikavälillä [A, B] on:

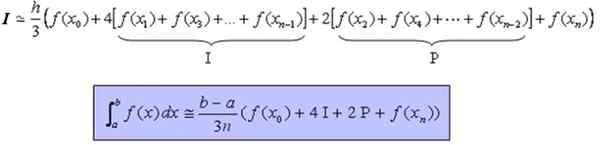
Esittely

Simpson -kaavan saamiseksi jokaisessa subintervalissa [xi, xi+2] funktio F (x) lähestyy toisen asteen P (x) polynomia (vertaus), joka kulkee kolmen pisteen läpi: [xi, F (F (F (F (f (F (F (F (F [Xi+1, f (xi+1)] ja [xi+2, f (xi+2)]]]].

Sitten integraali polynomi P (x) lasketaan [xi, xi+2], joka lähestyy funktion f (x) integraalia tällä aikavälillä.

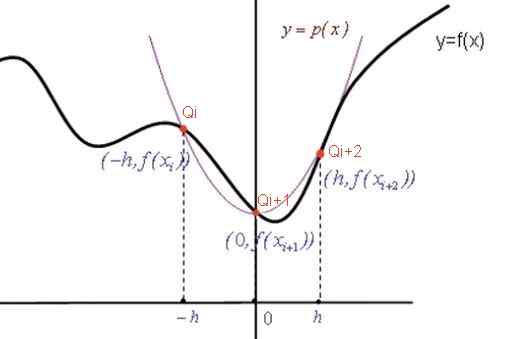Kuva 2. Kuvaaja Simpsonin kaavan osoittamiseksi. Lähde: f. Zapata.

Interpolointi polynomikertoimet

Parabola -yhtälöllä P (x) on yleinen muoto: p (x) = a x² + B x + c. Kun vertaus käy läpi punaisella (katso kuva) osoittamat pisteet, sitten kertoimet A, B, C määritetään seuraavasta yhtälöjärjestelmästä:

A (-h)² - B H + C = F (xi)

C = F (xi+1)

A (h)² + B H + C = F (xi + 2)

Voidaan havaita, että kerroin C määritetään. Kertoimen määrittämiseksi lisäämme ensimmäisen ja kolmannen yhtälön saadaan:

2 a h² + 2 c = f (xi) + f (xi + 2).

Sitten C: n arvo korvataan ja on selvää:

A = [f (xi) - 2 f (xi+1)+f (xi+2)] / (2 h²-A

Kerroin B määrittämiseksi ensimmäisen kolmas yhtälö vähennetään ja B puhdistaa itsensä:

B = [f (xi+2) - f (xi)] = 2 h.

Yhteenvetona voidaan todeta, että toisen asteen polynomi P (x), joka kulkee pisteiden Qi, Qi+1 ja Qi+2, on kertoimet:

A = [f (xi) - 2 f (xi+1)+f (xi+2)] / (2 h²-A

B = [f (xi+2) - f (xi)] = 2 h

C = F (xi+1)

Likimääräisen integraalin laskeminen [xi, xi+2]

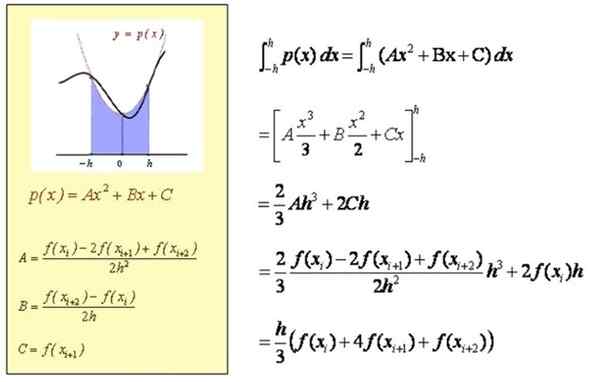
Arvioitu laskelma integraalista [A, B]

Kuten jo on sanottu, kokonaisella integraatiovälillä [a, b] osio x0, x1, x2,…, xn -1, xn vaiheella H = xi+1 - xi = (b - (b -) / n, missä n on pari.

Voi palvella sinua: näytteenottovirhe: kaavat ja yhtälöt, laskenta, esimerkit

Sitten kokonaisvälillä [A, B] määritelty integraali on subintervals -integraalien summa [xi, xi+2], joita lähestytään interpolointipolynomien P (x) integraalit: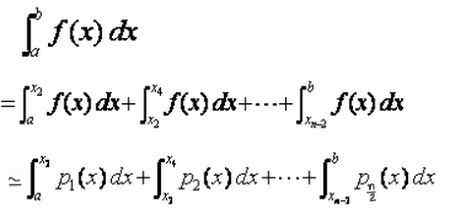

Edellisessä osassa löydettiin kaava polynomi -integraalien suhteen. Tämän tuloksen soveltaminen jokaiseen integraaliin on: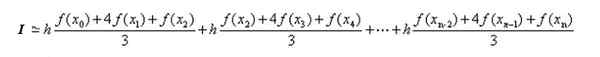

Joka voidaan kirjoittaa uudelleen kompaktilla tavalla seuraavasti: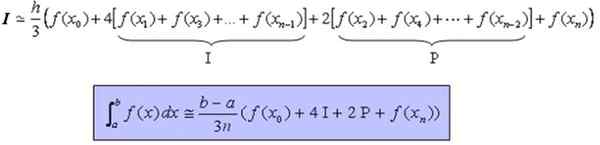

Lähestymisvirhe

Jos toiminto, johon haluat integroida aikaväliin [A, B], on johdettu neljänteen järjestykseen, jatkuvan kyseisessä aikavälillä, niin on mahdollista löytää kaava, jonka avulla lähestymistapa määritetään lähestymistavalla tavalla niistä Simpson SN -kaava Integraalin arvolle: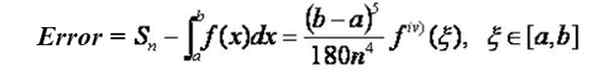

Huomaa, että virhe pienenee intervalli -alajakojen lukumäärän neljännellä voimalla. Esimerkiksi, jos siirryt N -alaosastoista 2N: ään, virhe vähenee 1/16 tekijällä.

Simpson -lähestymistavalla saatu ylempi virhetaso voidaan saada samasta kaavasta korvaamalla neljännen johdannaisen neljännen johdannaisen maksimaalisen absoluuttisen arvon väliaikalla [a, b].

Ratkaistu esimerkki

- Esimerkki 1

Harkitse funktiota f (x) = 1 / (1 + x²-A. 

Löydä F (x) -funktion määritelty integraali aikavälillä [-1, 1] käyttämällä Simpson-menetelmää kahdella alajaolla (n = 2).

Ratkaisu 

Otetaan n = 2. Integraatiorajat ovat a = -1 ja b = -2, sitten osio on tällainen: 

X0 = -1; X1 = 0 ja x2 = +1.

Siksi Simpsonin kaava hyväksyy seuraavasti:

N = 2 → xo = -1, x1 = 0; x2 = 1, siksi:

- Esimerkki 2

Harkitse funktiota f (x) = 1 / (1 + x²-A. 

Löydä funktion f (x) määritelty integraali Simpson-kaavan avulla neljällä alajaolla (n = 4).

Se voi palvella sinua: arviointia välein

Ratkaisu 

Otetaan n = 4. Integraatiorajat ovat a = -1 ja b = -2, sitten osio on tällainen: 

X0 = -1; X1 = -1/2; X2 = 0; X3 = 1/2 ja x4 = +1.

Simpsonin kaava on perustettu seuraavasti:

Integraali ≃ [(b -a)/(3 n)] [f (x0) + 4 i + 2 p + f (xn)]

Tapauksessa, jossa sitä sovelletaan, se on seuraava:

Integraali ≃ (1- (1))/(3⋅4)] [f (-1) + 4 [f (-½) + f (½)] + 2 [f (0)] + f (1)

Integraali ≃ (2/12) [½ + 4 (⅘ + ⅘) + 2⋅1 + ½] = (⅙) [47/5] = 47/30 = 1,5666

- Esimerkki 3

Määritä aikaisempien esimerkkien määritelty integraali tarkalleen ja tee vertailu tarkalle tulokselle Simpson -kaavan saamien esimerkkien 1a ja 1b saamien kanssa.

Ratkaisu 

Funktion f (x) = 1 / (1 + x: n määrittelemätön integraali²) on funktio Arctan (x).

Arvioitaessa integraatiorajoituksia:

Integraali = arctan (1) - arctan (-1) = π/4 - (-π/4) = π/2 = 1,5708

Jos verrataan tarkan ratkaisun tulosta Simpson -menetelmällä saatuna n = 2: lla ja n = 4: llä, meillä on:

N = 2: n erot tarkan ja likimääräisen ratkaisun välillä on π/2 -5/3 = -0959, toisin sanoen prosentuaalinen ero -0,06%.

Ja Simpson -lähestymistavalla n = 4: n kanssa tarkan ja likimääräisen ratkaisun välinen ero on π/2 - 47/30 = 0,0041, toisin sanoen prosentuaalinen ero 0,003%.

Ehdotettu harjoitus

Simpsonin menetelmä soveltuu soveltamiseen matemaattisiin laskelmiin suunnattuihin ohjelmointikieliin ja tietokonesovelluksiin. Se ehdotetaan lukijalle, joka tässä artikkelissa annettujen kaavojen perusteella kirjoita oman koodinsa suosikki -ohjelmaansa.

Seuraava kuva näyttää harjoituksen, jossa Simpson -kaava on toteutettu SMATH -Studio, Ilmainen ohjelmisto käytettävissä käyttöjärjestelmille Ikkunat ja Androidi.

Kuva 3. Esimerkki numeerisesta integraatiosta Simpson -säännön kautta ohjelmistolla. Lähde: f. Zapata.

Viitteet

1. Casteleiro, J. M. 2002. Kattava laskelma (kuvitettu painos). Madrid: ESIC -toimitus.
2. Tupla. Simpson -menetelmä. Valencian ammattikorkeakoulu. Palautettu: YouTube.com
3. Purcell, E. 2007. Yhdeksäs painoslaskelma. Prentice Hall.
4. Wikipedia. Simpson -hallinto. Palautettu: on.Wikipedia.com
5. Wikipedia. Lagrange -polynomi -interpolointi. Palautettu: on.Wikipedia.com