Sturges -hallinto

Selitämme, mikä Sturges -sääntö on, sen soveltaminen ja annamme useita esimerkkejä

Mikä on Sturges -sääntö?

Se Sturges -hallinto Se on kriteeri, jota käytetään luokkien tai väliajojen lukumäärän määrittämiseen. Saksalainen matemaatikko Herbert Sturges totesi tämän säännön vuonna 1926.

Sturges ehdotti yksinkertaista menetelmää, joka perustuu X -näytteiden lukumäärään, joiden ansiosta päästiin luokkien lukumäärän ja niiden alueiden lukumäärän. Sturges -sääntöä käytetään laajasti ennen kaikkea tilastoalueella, erityisesti taajuushistogrammien rakentamiseksi.

Selitys

Sturges -sääntö on empiirinen menetelmä.

Periaatteessa tämä sääntö määrittää graafisten säiliöiden leveyden, taajuushistogrammit.

Säännönsä määrittämiseksi Herbert Sturges piti ihanteellisena taajuuskaaviona, joka koostuu K -välineistä, joissa I -tämä aika sisältää tietyn määrän näytteitä (i = 0,… k - 1), esitettynä seuraavasti:

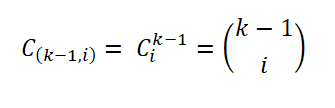
Tämä näytteiden lukumäärä annetaan niiden tapojen lukumäärän perusteella, joilla joukon alajoukko voidaan purkaa; Eli binomikerroin ilmaistaan ​​seuraavasti:

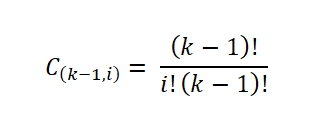Sitten Sturges liittyi siihen, että taajuushistogrammi lähestyy normaalia jakautumista, kun väliajojen lukumäärä (k) kasvaa rajan keskuslauseen mukaan. Siten, että kunkin väliajojen näytteiden lukumäärä voidaan laskea:

Se voi palvella sinua: Enegon: Ominaisuudet, miten tehdä enegon, esimerkkejä

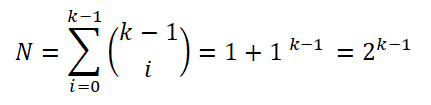
Lauseen yksinkertaistamiseksi hän käytti logaritmien ominaisuuksia yhtälön molemmissa osissa:

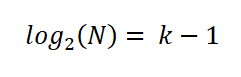
Siten Sturges osoitti, että lausekkeella annetaan optimaalinen lukujen lukumäärä:

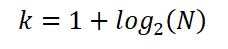
Se voidaan myös ilmaista seuraavasti:

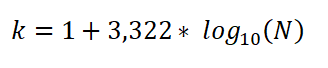
Tässä ilmaisussa:

• K on luokkien lukumäärä.
• N on näytteen havaintojen kokonaismäärä.
• Loki on yleinen peruslogaritmi 10.

Esimerkiksi taajuushistogrammin laatimiseksi, joka ilmaisee satunnaisen näytteen 142 lapsen asemasta, jakauman väliajojen tai luokkien lukumäärä on:

K = 1 + 3,322 _* Hirsi₁₀ (N)

K = 1+3,322_* Loki (142)

K = 1+3,322_* 2 1523

K = 8,14 ≈ 8

Siten jakauma on 8 väliajoa.

Väliajojen lukumäärä on aina edustettava kokonaislukuilla. Tapauksissa, joissa arvo on desimaalin tarkkuudella, lähimpään kokonaislukuun on tehtävä likiarvo.

Sturges -sääntöhakemukset

Sturges -sääntöä sovelletaan pääasiassa tilastoissa, koska se sallii taajuuden jakautumisen laskemalla luokkien lukumäärän (k), samoin kuin kunkin pituus, joka tunnetaan myös nimellä amplitudi.

Amplitudi on ero luokan ylä- ja alarajassa jaettuna luokkien lukumäärällä, ja se ilmaistaan:

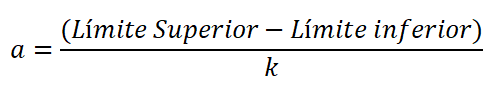
On monia empiirisiä sääntöjä, jotka sallivat taajuuden jakautumisen. Sturges -sääntöä käytetään kuitenkin yleisesti, koska se tekee lähestymistavan luokkien lukumäärää, joka yleensä menee 5: stä 15: een.

Tällä tavalla se pitää arvoa, joka edustaa oikein otosta tai väestöä; Toisin sanoen lähestymistapa ei edusta äärimmäisiä ryhmiä, eikä se toimi liiallisen määrän luokkien kanssa, jotka eivät salli tiivistää näytettä.

Se voi palvella sinua: vastakkaiset kulmat kärjen kautta (ratkaistu harjoitus)

Esimerkki

Taajuushistogrammi on suoritettava annetun tiedon mukaan, joka vastaa paikallisessa kuntosalissa harjoittaneiden miesten tutkimuksessa saatuja ikäryhmiä.

Väliajojen määrittämiseksi näytteen koko tai havaintojen lukumäärä tulisi tiedetä; Tässä tapauksessa niitä on 30.

Silloin Sturges -sääntö sovelletaan:

K = 1 + 3,322 _* Hirsi₁₀ (N)

K = 1+3,322_* Loki (30)

K = 1+3,322_* 1 4771

K = 5,90 ≈ 6 väliaika.

Väliajojen lukumäärästä voit laskea niiden amplitudin; Eli kunkin tangon leveys, joka on esitetty taajuushistogrammissa:

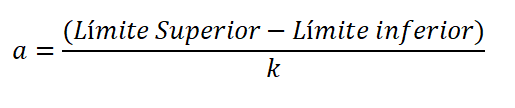
Alarajaa pidetään datan alhaisemman arvona, ja ylempi on korkein arvo. Eroa ylä- ja alarajan välillä kutsutaan muuttujan alueeksi tai reittiä (R).

Taulukossa on, että yläraja on 46 ja alempi 13; Tällä tavalla kunkin luokan amplitudi on:

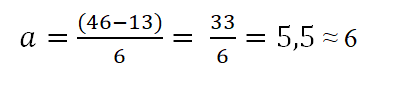
Välit koostuvat ylärajasta. Näiden väliajojen määrittämiseksi se alkaa laskemalla alarajasta, lisäämällä tähän sääntöllä (6) määritetty amplitudi seuraavasti:

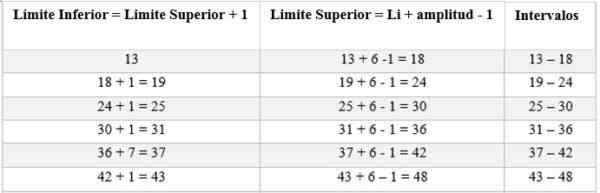
Sitten absoluuttinen taajuus lasketaan määrittämään kutakin aikaväliä vastaavien miesten lukumäärä; Tässä tapauksessa se on:

• Väli 1: 13 - 18 = 9
• Väli 2: 19 - 24 = 9
• Väli 3: 25 - 30 = 5
• Interval 4: 31 - 36 = 2
• Väli 5: 37 - 42 = 2
• Väli 6: 43 - 48 = 3

Lisäämällä kunkin luokan absoluuttinen taajuus, tämän on oltava yhtä suuri kuin näytteen kokonaismäärä; Tässä tapauksessa 30.

Voi palvella sinua: negatiivinen homotecia

Myöhemmin lasketaan kunkin aikavälin suhteellinen taajuus jakamalla tämän absoluuttinen taajuus havaintojen kokonaismäärällä:

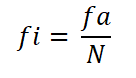
• Väli 1: FI = 9 ÷ 30 = 0,30
• Väli 2: FI = 9 ÷ 30 = 0,30
• Väli 3: FI = 5 ÷ 30 = 0,1666
• Väli 4: FI = 2 ÷ 30 = 0,0666
• Väli 5: FI = 2 ÷ 30 = 0,0666
• Väli 4: FI = 3 ÷ 30 = 0,10

Sitten voit tehdä taulukon, joka heijastaa tietoja, ja myös suhteellisen taajuuden kaavio suhteessa saatuihin väliajoihin, kuten seuraavissa kuvissa voidaan nähdä:

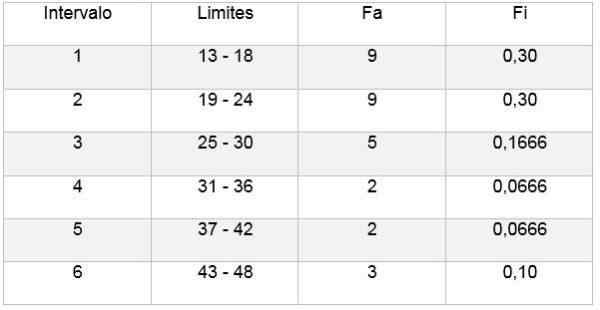
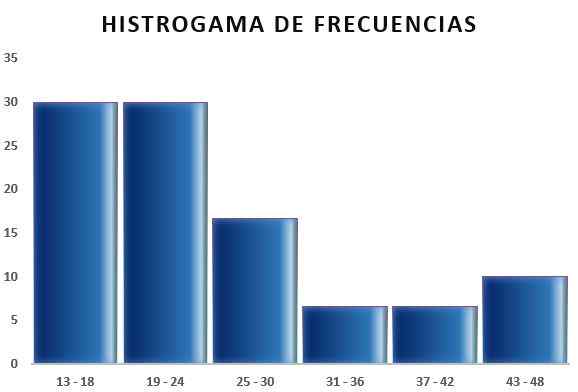
Tällä tavoin Sturges -sääntö mahdollistaa luokkien tai väliajojen lukumäärän määrittämisen, joihin näyte voidaan jakaa, jotta voidaan tehdä tiivistelmä datanäytteestä taulukoiden ja grafiikan kehittämisen kautta.