Suhteellisuussuhteiden käsite, esimerkit ja harjoitukset

Se Suhteellisuussuhteet Nämä ovat linkkejä kahden tai useamman muuttujan välillä, niin että kun yksi määristä vaihtelee, samoin kuin muiden arvo. Esimerkiksi, jos joku kasvaa, toiset voivat lisätä tai vähentää, mutta yhtenäisessä määrässä.

Muinaiskreikkalaiset matemaatikot huomasivat, että jotkut muuttujat liittyivät erittäin tarkasti. He tajusivat, että jos ympyrä on kaksinkertainen halkaisija kuin toinen, siinä on ympyrä, jolla on kaksinkertainen pituus.

Kuvio 1. Ympyrän pituus on suoraan verrannollinen sen halkaisijaan D. Lähde: f. Zapata

Ja jos halkaisija kolminkertaistuu, kehän muoto myös kolminkertaistaa. Tämä tarkoittaa, että halkaisijan nousu tuottaa kehän koon suhteellisen nousun.

Ja niin voimme vakuuttaa, että kehän L pituus on verrannollinen niiden halkaisijaan D, joka ilmaistaan ​​seuraavasti:

L ∝ d

Missä symboli ∝ luetaan "suoraan verrannollinen jhk". Tasa -arvon suhteellisuussymbolin muuttamiseksi ja numeeristen arvojen sisällyttämiseksi on välttämätöntä määrittää muuttujien välinen yhteys, jota kutsutaan suhteellisuusvakio.

Monien mittausten tekemisen jälkeen muinaiset matemaatikot totesivat, että kehän koon L välinen suhteellisuusvakio ja niiden halkaisija D oli numero 3.1416… Suspensat osoittavat äärettömän määrän desimaaleja.

Tämä arvo ei ole kukaan muu kuin kuuluisan numeron π (pi) ja tällä tavalla kirjoitamme:

L = π.D -d

Tällä tavoin syyn pituuden ja halkaisijan välillä on sama kuin syy toisen pituuden ja halkaisijan välillä. Ja parasta on, että meillä on nyt tapa laskea minkä tahansa kehän pituus vain tietämällä sen halkaisija.

[TOC]

Esimerkkejä suhteellisuussuhteista

Tieteessä (ja myös jokapäiväisessä elämässä) on erittäin tärkeää löytää muuttujien välisiä suhteita, tietää, kuinka toiseen muutokset vaikuttavat toiseen. Esimerkiksi:

Voi palvella sinua: kuinka monta halkaisijaa kehällä on?

-Jos tehdä kymmenen evästettä, tarvitaan 3 jauhokuppia. Kuinka monta kuppia tarvitaan 2: n ja puoli kymmenen tekemiseen?.

-Tietäen, että elohopea planeetalla esine painaa 4 kertaa vähemmän kuin maan päällä, kuinka paljon 1 auto elohopeassa.5 tonnia?

-Kuinka muutos voiman kiihtyvyyteen kohdistuvassa voimassa, johon sitä sovelletaan, vaikuttaa?

-Jos ajoneuvo kulkee moottoritiellä yhtenäisellä suorakulmiolla ja tiedämme, että se kulkee 30 km 10 minuutissa, mikä on 20 minuutin kuluttua kulunut etäisyys?

-Kun meillä on lanka, jonka läpi sähkövirta on läpi, miten sen välinen jännite vaihtelee, jos se kasvaa?

-Jos ympyrän halkaisija kaksinkertaistuu, miten alueesi vaikuttaa?

-Kuinka etäisyys täsmällisellä kuormituksella tuotetun sähkökentän intensiteettiin vaikuttaa?

Vastaus on suhteellisuussuhteissa, mutta kaikki suhteet eivät ole samantyyppisiä. Sitten löydämme ne kaikista täältä esitetyistä tilanteista.

Suora suhteellisuus ja käänteinen suhteellisuus

Kaksi muuttujaa x ja y ovat suorassa suhteessa, jos ne liittyvät:

y = kx

Missä k on suhteellisuusvakio. Esimerkki on jauhojen ja evästeiden määrien välinen suhde. Jos piirrämme nämä muuttujat, saadaan suora viiva kuvassa esitetyllä tavalla:

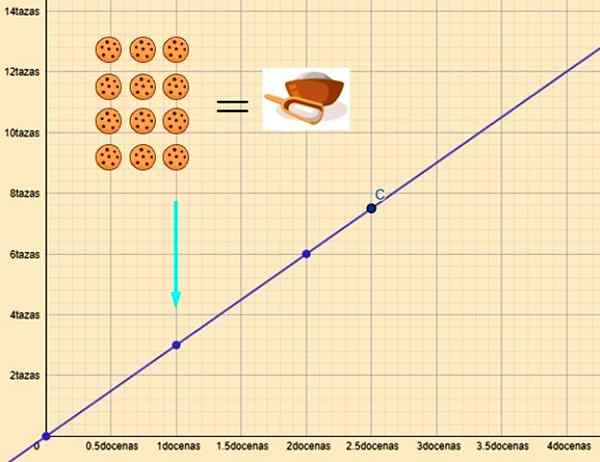Kuva 2. Tehdä 2.5 tusinaa evästettä tarvitsevat 7.5 jauhokuppia (kohta C). Lähde: f. Zapata.

Kyllä ja ovat jauhokupit ja x kymmeniä evästeitä, niiden välinen suhde on:

y = 3x

X = 1 tusina tarvitsemme y = 3 kuppia jauhoja. Ja x = 2: lle.Vaaditaan 5 tusinaa, y = 7.5 jauhokuppia.

Se voi palvella sinua: 8 tyyppiä mittausvirheitä (esimerkkien kanssa)

Mutta meillä on myös:

-Kiihtyvyys -lla että ruumiin kokemat ovat verrannollinen voimaan F joka toimii hänen kanssaan, koska se on kehon massa, jota kutsutaan m, Suhteellisuusvakio:

F = m-lla

Siksi mitä suurempi sovellettu voima, sitä suurempi kiihtyvyys tuotettu.

-Ohmisissa johtimissa V -jännite sen päiden välillä on verrannollinen käytettyyn virtaan ja. Suhteellisuusvakio on kuljettajan vastus:

V = ri

-Kun esine liikkuu yhtenäisen suorasuntelon liikkeellä, etäisyys d -d on verrannollinen aikaan t, nopeus v Suhteellisuusvakio:

d = v.t

Joskus löydämme kaksi määrää siten, että A: n lisääntyminen a vähentää suhteessa toiseen. Tätä yksikköä kutsutaan Käänteinen osa.

Esimerkiksi edellisessä yhtälössä tietyn etäisyyden D kuluttamiseen tarvittava aika T on käänteisesti verrannollinen reitin nopeuteen v:

T = d/v

Ja niin, mitä suurempi nopeus v, sitä vähemmän aikaa auto vie etäisyyden D matkustamiseen. Jos nopeus esimerkiksi kaksinkertaistuu, aika vähenee puoleen.

Kun kaksi muuttujaa x ja y ovat päinvastaisessa suhteessa, voimme kirjoittaa:

y = k / x

On suhteellisuusvakio. Tämän yksikön kaavio on:

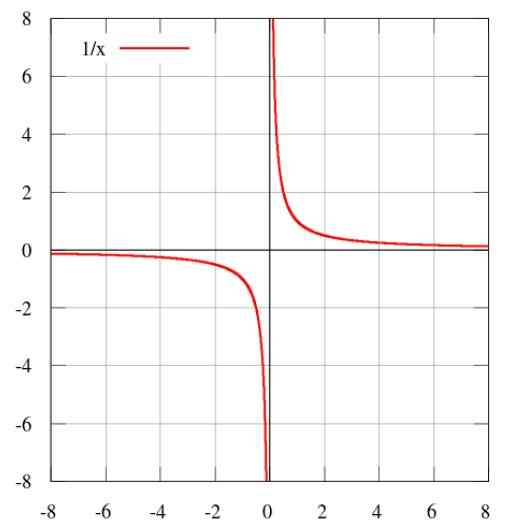
Kuva 3. 1/x -kuvaaja, joka edustaa käänteistä suhteellisuutta. Lähde: Wikimedia Commons.

Muun tyyppiset suhteellisuus

Yhdessä aiemmin mainituissa esimerkeissä kysyimme itseltämme, mitä tapahtuu ympyrän alueella, kun säde kasvaa. Vastaus on, että pinta -ala on suoraan verrannollinen säteen neliöön, suhteellisuusvakio on π:

A = πr²

Jos säde kaksinkertaistuu, pinta -ala kasvaa tekijällä 4.

Ja sähkökentän tapauksessa JA tuotettu täsmällinen kuorma Q -, On tiedossa, että intensiteetti vähenee käänteisen etäisyyden neliön kanssa r - kuormitukseen Q --

E = k_ja Q/R²

Voi palvella sinua: Miksi algebra on tärkeä tietyissä päivittäisessä tilanteessa?

Mutta voimme myös vakuuttaa, että kentän voimakkuus on suoraan verrannollinen kuorman suuruuteen, koska se on suhteellisuuden vakio k_ja, Sähköstaattinen vakio.

Muita tieteessä esiintyviä suhteellisuuksia ovat eksponentiaalinen suhteellisuus ja logaritminen suhteellisuus. Ensimmäisessä tapauksessa muuttujat x ja y liittyvät:

y = k.-lla^x

Missä a on pohja, positiivinen määrä 0, joka on yleensä 10 tai luku E. Esimerkiksi bakteerien eksponentiaalisella kasvulla on tämä muoto.

Toisessa tapauksessa muuttujien välinen suhde on:

y = k.Hirsi_-lla x

Jälleen A on logaritmin pohja, joka on usein 10 (desimaalilogaritmi) tai E (Neperian logaritmi).

Harjoitukset

- Harjoitus 1

Tietäen, että elohopea planeetalla esine painaa 4 kertaa vähemmän kuin maan päällä, kuinka paljon 1 auto elohopeassa olisi.5 tonnia?

Ratkaisu  

Elohopeapaino = (1/4) paino maalla = (1/4) x 1.5 tonnia = 0.375 tonnia.

- Harjoitus 2

Juhlia varten jotkut ystävät päättävät valmistaa mehua hedelmällisestä tiivisteestä. Pakkausohjeissa sanotaan, että 15 lasillista mehua on valmistettu lasillisesta tiivisteestä. Kuinka paljon keskittyä tarvitaan 110 lasillisen mehun valmistamiseksi?

Ratkaisu

Anna ja mehu ja x -alusten määrä tiivisteiden suonien määrä. Ne liittyvät:

y = kx

Kun korvaavat arvot y = 15 ja x = 1, vakio K puhdistetaan:

K = y/x = 15/1 = 15

Siksi:

110 = 15 x

x = 110/15 = 7.33 lasillista hedelmäkonsentraattia.

Viitteet

1. Baldor, a. 1974. Algebra. Venezuelan kulttuurinen s.-Lla.
2. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. Kuudes. Ed Prentice Hall.
3. Varsity -tutorit. Suhteellisuussuhteet. Haettu: WarsityTorm.com
4. Wikipedia. Suhteellisuus. Palautettu: on.Wikipedia.org.
5. Zill, D. 1984. Algebra ja trigonometria. McGraw Hill.