Kartiomaiset osiotyypit, sovellukset, esimerkit

Se kartiomaiset osat Ne ovat käyrät, jotka saadaan sieppaamalla tason kartioon. Tätä on useita tapoja; Esimerkiksi, jos taso siirretään kohtisuoraan kartion aksiaaliseen akseliin nähden, saadaan ympärysmitta.

Kolkutason kallistuminen hiukan kartion aksiaaliseen akseliin saadaan ellipsi, käyrä, joka on suljettu, mutta jos kietomme sen vielä enemmän parabolaa tai hyperbolaa, kuten voidaan nähdä kuvan 1 animaatiossa.

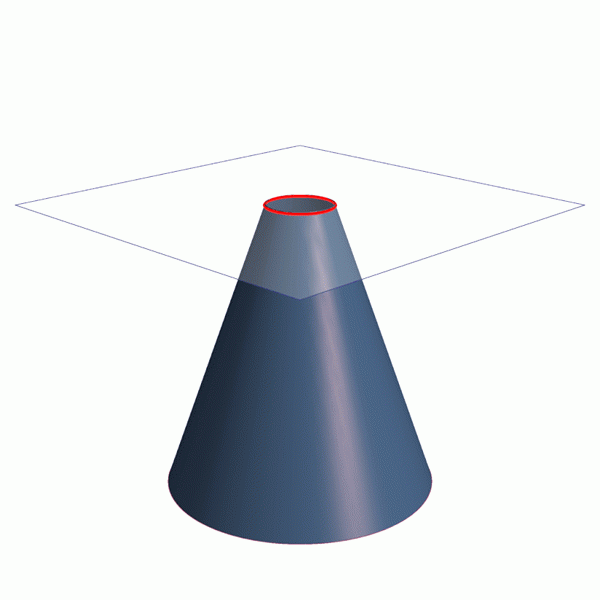Animaatio, joka osoittaa, kuinka saada neljä kartiomaista osaa: Ympyrä, vertaus- ja hyperbola Ellipse. Lähde: Wikimedia Commons. Linjat / cc0

Kartiomaiset osat ovat osa luontoa ja ympäröivää maailmaa. Suunnittelu, arkkitehtuuri ja tähtitiede ovat tärkeitä tietohaaroja, jotka käyttävät kartioita.

[TOC]

Kartiomaisten osien olosuhteet

Kartiomaiset osiot määritellään geometrisiksi paikoiksi, jotka täyttävät seuraavat ehdot:

Vertaus

Kaikkien kohtien geometrinen paikka on yhtäläistä tasossa kiinteään pisteeseen, nimeltään keskittyä F ja suora viiva myös kiinnitetty, nimeltään direktiivi.

Ellipsi

Tasopiste kuuluu ellipsiin, jos kyseisen pisteen ja kahden muun kiinteän kohdan välisten etäisyyksien summa, jota kutsutaan Keskittyä ja sijaitsee pääakseli ellipsistä pysyy vakiona.

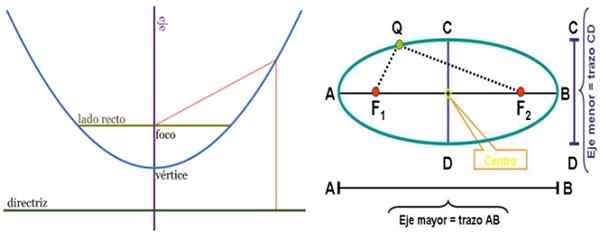Vasemmalla puolella oleva vertaus ja ellipsi oikealle, omilla elementeillä. Focit ovat pisteitä monissa sovelluksissa. Lähde: Wikimedia Commons.

Ympärysmitta

Kaikkien pisteiden geometrinen paikka ylläpitää saman etäisyyden toiseen pisteeseen nimeltä Centro. Tämä etäisyys on radio ympärysmitta.

Voi palvella sinua: Euklidian etäisyys: käsite, kaava, laskenta, esimerkki

Hyperbeli

Pistejoukko tasossa siten, että ero sen etäisyyden välillä kahteen kiinteään pisteeseen, nimeltään Keskittyä, se on vakio.

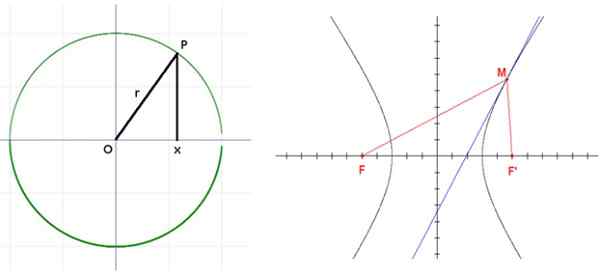Hyperbola foci f- ja f. Lähde: Wikimedia Commons.

Sovellukset

Katsotaanpa joitain kartiomaisia ​​osioiden sovelluksia:

Vertaukset  

-Kun esine käynnistetään, seuraavalla suuntauksella on vertausmuoto.

-Vertauksissa on merkittäviä tekniikan sovelluksia, esimerkiksi ripustetuissa siltoista kaapelit kiirehtivät vertausten muodossa.

-Vertaukset ovat myös hyviä, jotta heijastimet ja teleskoopit. Tämä on mielenkiintoisen ominaisuuden ansiosta: Kun asetetaan valaisinta parabolisen poikittaisen osion pinnan painopisteeseen, valo kulkee samansuuntaisesti vertauksen akselin kanssa.

-Jos symmetria -akselin yhdensuuntaiset valoisat säteet lähestyvät parabolista pintaa, se keskittää ne tarkennukseen, olosuhteet, joita käytetään heijastimen teleskoopien, kuten Hale de Monte Palomar -teleskoopin, valmistukseen.

Ellipsit

-Aurinkojärjestelmän planeetat liikkuvat elliptisten suuntausten jälkeen, melko lähellä kehää suurten planeettojen tapauksessa, maa sisältyy. Aurinko ei ole keskellä, vaan yhdessä valokeilassa.

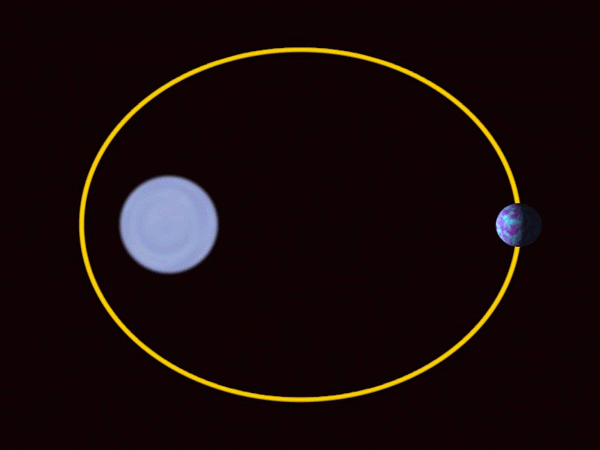Aurinkojärjestelmän planeetat liikkuvat elliptisissä kiertoradalla auringon kanssa yhdessä valokeilassa. Lähde: Wikimedia Commons.

-Ellipsiä käytetään laajasti arkkitehtuurissa koriste- ja suunnitteluelementteinä.

-Asettamalla heijastin johonkin ellipsin valokeilaan, valo heijastuu kohti toista keskittymistä. Sama tapahtuu äänen kanssa. Siksi Ellipsen muotoiset hallit, jotka puhuvat hiljaa yhdessä keskittymisessä yhdessä keskittymisessä, kuulevat selvästi toisessa tarkennuksessa.

Se voi palvella sinua: hepagonaalinen prisma

-Sama ominaisuus on yllättävä sovellus lääketieteen alalla. Munuaislaskelmat voidaan tuhota äänellä. Suuren voimakkuuden ultraääniaallot syntyvät yhdessä vettä täynnä olevan elliptisen kylpyammeen polttoaineista, ja potilas sijaitsee toisessa tarkennuksessa. Ääniaallot vaikuttavat ja heijastavat laskelmassa, ja energiansa avulla ne pirstoutuvat pieninä kappaleina, jotka henkilö sitten karkottaa helposti virtsaamisen aikana.

Hyperbolat

-Jotkut aurinkokunnan komeetit seuraavat hyperbolisia suuntauksia, aina auringon ollessa yhdessä fokusissa.

-Hyperbolas -keskittymät ovat myös erittäin mielenkiintoisia tutkimaan aallon heijastuksen ilmiöitä. Esimerkiksi ohjaamalla valonsäde parabolisen peilin keskittymiseen, se heijastuu toisessa painopisteessä, erittäin hyödyllinen ominaisuus teleskoopien rakentamiselle, koska valo voi keskittyä paraboliseen peiliin ja ohjata toiseen sopivampaan paikkaan Suunnittelun mukaan.

-Ydinlaitosten jäähdytystornissa on hyperbolas -muotoinen siluetti.

-Ennen GPS: n tulemista hyperboloja käytettiin navigoinnissa veneiden löytämiseksi. Radio A- ja B -asemilla samanaikaisesti antamat aluksen signaalit ja tietokone oli vastuussa signaalien saapumisaikojen erojen rekisteröinnistä, niiden muuttamiseksi etäisyyksien eroiksi etäisyyseroista. Tällä tavalla alus sijaitsee hyperbolan haarassa.

Menettely toistetaan kahdella muulla radio C- ja D -asemalla, jotka asettavat aluksen haaraan Toinen hyperbola. Veneen lopullinen sijainti on molempien hyperbolien leikkauspiste.

Voi palvella sinua: Kasvava toiminto: Kuinka tunnistaa se, esimerkkejä, harjoituksia

Ympärysmitta

-Pyörän saapuminen muutti historian kulkua.

-Pyöreä liike on hyvin yleinen, monet kappaleet pyörivät tuottamaan erilaisia ​​vaikutuksia tehtaista faneihin.

-Vaikka tärkeimpien planeettojen suuntaukset ovat elliptisiä, pyöreät radat ovat monissa tapauksissa hyviä lähestymistapoja.

-Levynferenssit ovat usein arkkitehtuurin, suunnittelun, suunnittelun ja rakentamisen elementtejä. Pyöreiden tai levymuotojen luettelo on loputon: kolikot, CD -levyt, kellot ja muut.

Esimerkit

Sitten koneessa on kaksi kartiomaista, ympyrä ja ellipsi.

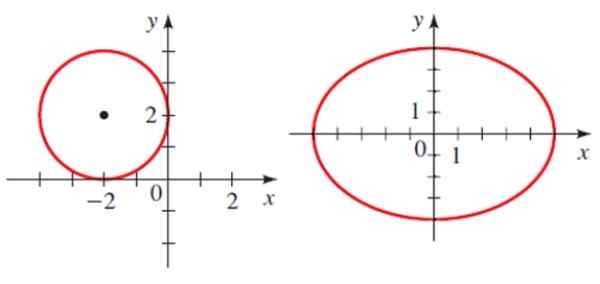Esimerkkejä kartiomaisista osista: ympyrä ja ellipsi. Lähde: Stewart, J. Ennakkoluulo.

Jokaisella on analyyttinen yhtälö:

Ympärysmitta

(X-H)² + (Y-K)² = R²

Missä H ja K ovat keskuksen koordinaatit ja R on radio. Kuvassa esitetyn ympärysmitana yhtälö on:

(x+2)² + (Y-2)² = 4

Ellipsi

Ellipse -yhtälö, jonka keskus on koordinaattipiste (H, K):

[(X-H)² /² ]+ [(y-k)² /b² ] = 1

Missä a ja b ovat ellipsin puolijohtopiles. Esitetylle ellipselle keskus on pisteessä 0,0, suurin puoliksi -sama on sama ja pieni puolipiste on 4. Siksi sen yhtälö on:

(x² /25)+ (ja² / 16) = 1

Viitteet

1. Hoffman, J. Matematiikan aiheiden valinta. Nide 2.
2. Jiménez, r. 2008. Algebra. Prentice Hall.
3. Stewart, J. 2006. Precculment: Laskentamatematiikka. Viides. Painos. Cengage -oppiminen.
4. Wikipedia. Kartiohäiriö. Palautettu: on.Wikipedia.org.
5. Zill, D. 1984. Algebra ja trigonometria. McGraw Hill.