Puolipyörä kuinka kehä, pinta -ala, keskikohdan, harjoitukset lasketaan

Hän puolipyöreä Se on litteä kuva, joka on rajamassa kehän halkaisija ja toinen kahdesta litteästä pyöreästä kaarista, jotka määritetään mainitulla halkaisijalla.

Tällä tavoin puolipyöreä on a puolijohto, joka koostuu tasaisesta pyöreästä kaarista ja suorasta segmentistä, joka liittyy tasaisen pyöreän kaarin päihin. Puolipyörä peittää puolipyörän ja kaikki sisätilat osoittavat samaan.

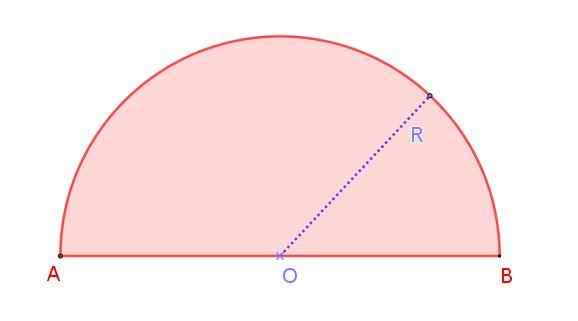Kuvio 1. Radio R -radio -puolivälissä. Lähde: f. Zapata.

Voimme nähdä tämän kuvassa 1, joka näyttää radio r rión r: n, jonka mitta on puolet halkaisijasta AB. Huomaa, että toisin kuin ympyrä, jossa on äärettömiä halkaisijoita, puolipyörissä on vain yksi halkaisija.

Puolipyörä on geometrinen hahmo, jolla on monia käyttötarkoituksia arkkitehtuurissa ja suunnittelussa, kuten seuraavassa kuvassa näemme:

Kuva 2. Seminicírculo arkkitehtuurin koriste -elementtinä. Lähde: Pikisti.

[TOC]

Puolipyörän elementit ja mittaukset

Puolipyörän elementit ovat:

1.- Litteä pyöreä kaari A⌒B

2.- Segmentti [AB] 

3.- Sisustus osoittaa puolipyöränsä, joka koostuu A⌒B -kaarista ja segmentistä [AB].

Puolipyörän kehä

Ympäristö on kaarin ja suoran segmentin summa, siksi:

Kehä = kaaren pituus A⌒B + segmentin pituus [AB]

Radio -puolipyörän r -kehä P annetaan kaavalla:

P = π⋅r + 2⋅R = (π + 2) ⋅R

Ensimmäinen termi on puolet säteen R -kehän kehästä, kun taas toinen on halkaisijan pituus, joka on kaksinkertainen säde.

Voi palvella sinua: lämpömittakaavat

Puolipyöreän pinta -ala

Puolipyöränä on yksi litteistä kulma -aloista, jotka jäävät piirtämällä halkaisija kehän läpi, sen pinta -ala on puolet ympyrän alueesta, joka sisältää radiopiryklin r:

A = (π⋅r²) / 2 = ½ π⋅R²

Puolipyörän keskikohta

Puolipyörän keskikohta on sen symmetrian akselilla korkeuteen, joka mitataan sen halkaisijasta 4/(3π), kun säde r.

Tämä vastaa noin 0,424⋅R: tä, mitattuna puolipyörän keskustasta ja sen symmetria -akselista, kuten kuviossa 3 esitetään.

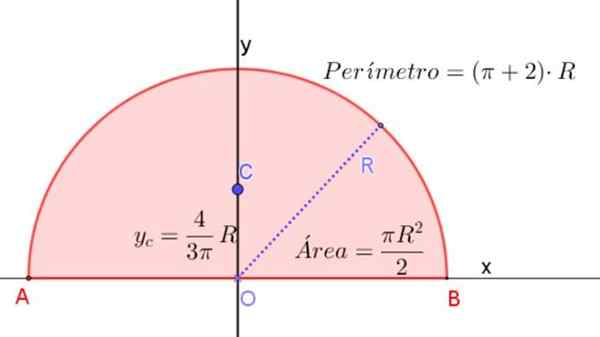Kuva 3. Radio R: n puoliympyrä, joka osoittaa kaavat sen keskikohdan ja sen keskikohdan sijainnin määrittämiseksi. Lähde: f. Zapata.

Puolipyörän hitausmomentti

Litteän kuvion hitausmomentti määritetään suhteessa akseliin, esimerkiksi X -akseliin, kuten:

Akseliin kuuluvien pisteiden etäisyyden etäisyyden neliön integraali, integraatioero on ääretön pinta -ala, joka on otettu kunkin pisteen asentoon. 

Kuvio 4 näyttää hitausmomentin määritelmän I_x radion r: n puolipyörästä suhteessa X -akseliin, joka kulkee sen diagonaalin läpi:

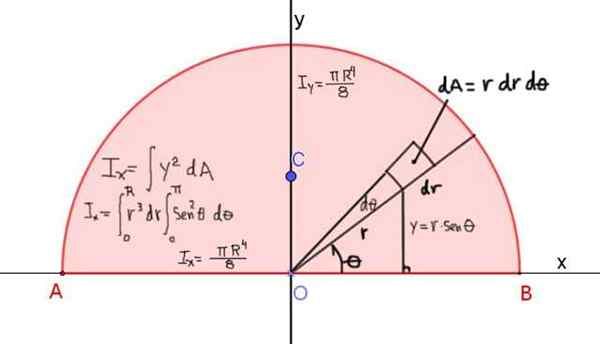Kuva 4. Puolipyörän hitausmomentin määritelmä suhteessa X -akseliin, joka kulkee sen diagonaalin läpi. Tulos on esitetty hitausmomentteina X- ja Y -akselien suhteen. Lähde: f. Zapata.

Hitausmomentti X -akselin suhteen annetaan:

Yllyttää_x = (π⋅r⁴) / 8

Ja hitausmomentti symmetrian akselin suhteen ja on:

Voi palvella sinua: aaltoileva optiikka

Iy = (π⋅r⁴) / 8

Se osoittaa, että molemmat hitausmomentit osuvat heidän kaavassaan, mutta on tärkeää korostaa, että niihin viitataan eri akseleihin.

Rekisteröity kulma

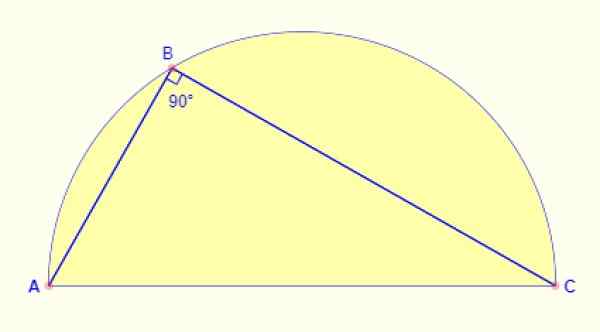
Puolipyörässä rekisteröity kulma on aina 90º. Riippumatta siitä, mikä kaaren osa vie pisteeseen, kuvion sivujen AB: n ja BC: n välinen kulma on aina suora.

Kuva 5. Puolipyöruun rekisteröity kulma. Lähde: Matematiikan avoin viite.

Ratkaisut

Harjoitus 1 

Määritä 10 cm: n säteen puolipyöreän kehä.

Ratkaisu

Muista, että sädeestä riippuen kehä annetaan aiemmin näkemämme kaavalla:

P = (2 + π) ⋅R

P = (2 + 3,14) ⋅ 10 cm = 5,14 ⋅ 10 cm = 51,4 cm.

Harjoitus 2

Löydä 10 cm: n radio -puolipyörän alue.

Ratkaisu

Puolipyörän alueen kaava on:

A = ½ π⋅R² = ½ π⋅ (10 cm)² = 50π cm² = 50 x 3,14 cm² = 157 cm².

Harjoitus 3

Määritä säteen keskuksen korkeus H puolipyörä r = 10 cm mitattuna sen pohjasta, sama on puolipyörän halkaisija. 

Ratkaisu

Keskusta on puolipyöreän tasapainopiste ja sen sijainti on symmetria -akselilla pohjan korkeudella H (puolipyörän halkaisija):

H = (4⋅R) / (3π) = (4⋅10 cm) / (3 x 3,14) = 4,246 cm

Harjoitus 4

Löydä puolipyörän hitausmomentti suhteessa sen halkaisijan kanssa samaan aikaan, tietäen, että puoliympyrä on valmistettu ohuesta arkista. Sen säde on 10 cm ja sen massa on 100 grammaa.

Ratkaisu

Kaava, joka antaa puolipyörän hitausmomentin, on:

Voi palvella sinua: Solid State Fysiikka: Ominaisuudet, rakenne, esimerkit

Yllyttää_x = (π⋅r⁴) / 8

Mutta koska ongelma kertoo meille, että se on materiaalinen puolipyöreä, niin edellinen suhde on kerrottava puolipyörän massaa pintatiheydellä, jota merkitään σ.

Yllyttää_x = σ (π⋅R⁴) / 8

Sitten määritämme σ, joka ei ole muuta kuin puolipyörän massa jaettuna saman alueen välillä.

Alue määritettiin harjoituksessa 2 ja tulos oli 157 cm². Sitten tämän puolipyörän pinnallinen tiheys on:

σ = 100 grammaa / 157 cm² = 0,637 g/cm²

Sitten halkaisijan hitausmomentti lasketaan seuraavasti:

Yllyttää_x = (0,637 g/cm²) [3,1416 ⋅ (10 cm)⁴]/ 8

Tuloksena:

Yllyttää_x = 2502 G⋅CM²

Harjoitus 5

Määritä säteen hitausmomentti, joka² akselilla, joka kulkee sen keskikohdan läpi ja on yhdensuuntainen sen halkaisijan kanssa.

Ratkaisu

Tämän harjoituksen ratkaisemiseksi on tarpeen muistaa Steinerin lause rinnakkaisten akselien hitaushetkinä, joissa sanotaan:

Hitausmomentti i suhteessa akseliin, joka on etäisyyden h: n etäisyydellä H -hitausmomentin I_c Akselista, joka kulkee keskikohdan läpi ja on yhdensuuntainen ensimmäisen kanssa taikinan tuote kahden akselin erottelun neliön läpi.

I = i_c + M H²

Meidän tapauksessamme tiedetään, että se on hitausmomentti halkaisijan suhteen, joka on jo laskettu harjoituksessa 4. H tietää myös halkaisijan ja keskikohdan välillä, joka laskettiin harjoituksessa 3.

Meidän on vain puhdistettava IC:

Yllyttää_c = I - m h²

Yllyttää_c = 2502 G⋅CM² - 100 g ⋅ (4 246 cm)² Tuloksena hitausmomentti akselilla, joka on yhdensuuntainen halkaisijan kanssa ja joka kulkee keskikohdan läpi, on: 

Yllyttää_c = 699,15 G⋅CM²

Viitteet

1. Alexander, D. 2013. Geometria. Viides. Painos. Cengage -oppiminen.
2. Matematiikan avoin viite. Puolipyöreä. Toipunut: MathPenref.com.
3. Maailmankaikkeuden kaavat.Puolipyöreä. Toipunut: UniversOformulat.com.
4. Maailmankaikkeuden kaavat. Puolipyöreän pinta -ala. Toipunut: UniversOformulat.com.
5. Wikipedia. Puolipyöreä. Haettu: vuonna.Wikipedia.com.