Fibonacci -sarjan ominaisuudet, luonnonsuhteet, sovellukset

Se O -sarja Fibonacci -peräkkäisyys on numerosekvenssi, joka saadaan aloittamalla arvolla 0 ja 1, jatkuu niiden summalla: 0 + 1 = 1, sitten kahden edellisen summa: 1 + 1 = 2 ja niin edelleen.

Tämän menettelyn mukaisesti saadaan muut termit, katsotaan: 2 + 1 = 3, 3 + 2 = 5, 5 + 3 = 8, 8 +5 = 13…

Fibonacci -sarjan ensimmäiset numerot

Menettely toistetaan niin monta kertaa kuin haluat. Tällä tavalla Fibonaccin peräkkäisyys hankkii lomakkeen: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 .. Numeroita, jotka tekevät siitä Fibonacci.

[TOC]

Historia

Fibonaccin peräkkäisyyttä kutsutaan italialaiseksi matemaatikkona, joka asui keskiajalla: Leonardo de Pisa, joka tunnetaan myös nimellä Fibonacci (1175-1250). 

Leonardo de Pisa

Leonardo vietti lapsuuden Pohjois -Afrikassa ja matkusti koko Välimerellä, missä hän tunsi Indo -arabisen numerointijärjestelmän ja oli iloinen hänestä. Todennäköisesti Leonardon arabiopettajat opettivat hänelle peräkkäisyydestä, jonka hindulaiset matemaatikot tunsivat jo.

Myöhemmin palattuaan Pisa Fibonacciin kirjoitti kirjan nimeltä Liber Abaci (Abacuksen kirja), jossa korostetaan indo -arabialaisten lukujen etuja roomalaisen numerointiin ja esittelyn 0 edessä, hän herätti ongelman kanien lisääntymisestä.

Ja ratkaisu tähän ongelmaan on juuri Fibonacci -peräkkäin numerot.

Leonardo de Pisa ei myönnetty peräkkäisen perustamisen luomiseen; Hän mainitsi sen vain kirjassaan uteliaisuutena, joka kiinnitti monien häntä seuranneiden tutkijoiden huomion. Näiden joukossa oli yhdeksännentoista vuosisadan ranskalainen matemaatikko Edouard Lucas, joka tutkiessaan hänet kastoi hänet keskiaikaisen salviaan, joka ilmoitti sen lännessä.

Fibonacci -kanien ongelma

Ongelmassa sanotaan: Ikuisesti asuu pari kania, mikä on kahden kuukauden ajan hedelmällinen. Kun kypsyys on saavutettu, heillä on joka kuukausi pari erilaista sukupuolen vauvaa, joiden lisääntyminen vie myös kaksi kuukautta ja kuukausittainen pari kani.

Voi palvella sinua: de Morgan -lakeja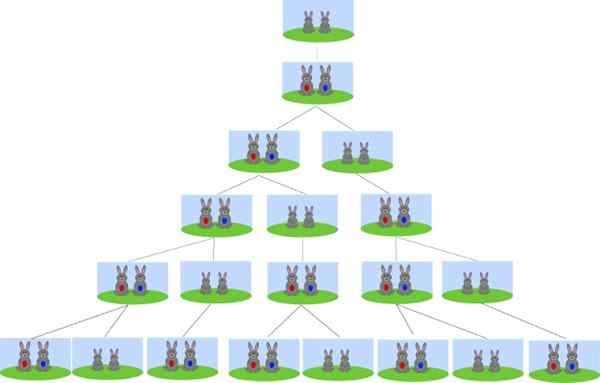Fibonaccin peräkkäisyyden alkuperä on kanien lisääntymisen ongelmassa. Lähde: Wikimedia Commons.

Alkaen parista vastasyntyneen kaniin, kuinka monta paria kaneja on kuukaudessa? Kuinka monta kaniparia on 2, 3 ja 4 kuukauden kuluttua? Ja kuinka monta tulee 6 kuukauden kuluttua?

Vastaus on fibonacci -numeroilla. Yhden kuukauden kuluttua on yksi kanipari, alkuperäinen pari, koska ne lisääntyvät vain 2 kuukauden kuluttua.

Kahden kuukauden kuluttua on 2 kaniparia: alkuperäinen pariskunta ja heidän ensimmäinen pentue.

Kolmen kuukauden kuluttua meillä on 3 paria, mukaan lukien alkuperäinen pari, heidän ensimmäinen pentue ja uusi.

Saavuttuaan 4. kuukauden, meillä on alkuperäinen pari, ensimmäinen pentue, jolla puolestaan ​​on ensimmäiset lapset, kolmannen kuukauden pentue ja uusi pentue. Kaikkiaan 5 paria kaneja.

Mutta nämä ovat Fibonacci -sekvenssin lukumäärät, joten 6 kuukauden kuluttua on 13 kanin paria, koska joka kuukausi lisätään kahden edellisen kuukauden parit.

Fibonacci -sarjan ominaisuudet

Tässä on joitain mielenkiintoisia ominaisuuksia Fibonacci -peräkkäisyydestä.

Omaisuus 1

Rekursiivinen kaava peräkkäisen ehtojen löytämiseksi on:

-lla_N+1 = a_n + -lla_N-1  N suurempi tai yhtä suuri kuin 2.

Missä n = 2, 3, 4,… eli seitsemäs termi a₇, Teemme n = 6, niin että 6+1 = 7. Meidän on tiedettävä ehdot₅  jo₆, luettelosta, joka ilmestyy johdannossa₅ = 5 ja a₆ = 8, siten₇ = 5+8 = 13.

Omaisuus 2

Jos kahta termiä, joita haluamme löytää, ei tunneta, voimme käyttää seuraavaa kaavaa:

Se voi palvella sinua: Tesseldos: Ominaisuus, tyypit (säännöllinen, epäsäännöllinen), esimerkkejä

Omaisuus 3

Numerot a_n jo_N+1 are  Likromit, Eli ne ovat serkkuja keskenään, mikä tarkoittaa, että heillä ei ole yhteisiä tekijöitä.

Omaisuus 4

Erittäin mielenkiintoinen ominaisuus on termien välillä_2N jo_n, joka on 1 arvoinen, kun n = 1. Tarkoittaen:

-lla₂ /₁ = 1

Voimme helposti tarkistaa sen Fibonacci -numeroiden luettelolla.

Toisaalta, jos n ≠ 1, osamäärä on:

-lla_2N /_n = a_n  + Toinen_N-1

Esimerkiksi jos n = 3, niin a _2N = a₆ = 8 ja₃ = 2. No sitten:

8/2 = 2 + 2. -lla₂ = 2 + 2. 1

Itse asiassa: 8/2 = 4 ja 2 + (2.1) = 4. Voidaan varmistaa, että mikä tahansa n -arvo saavutetaan.

Omaisuus 5

Suhde r_n = a_N+1 /_{n ,} Kun N tulee suureksi, lähentyä Kulta jompikumpi Aurea -osuus, Irrationaalinen luku, joka syntyy usein luonteeltaan, antanut:

Fibonacci -peräkkäisyyden luonnonsuhteet

Fibonaccin peräkkäisyys kasveissa

Fibonacci -peräkkäisyyden ilmenemismuodot on runsaasti kasvien valtakunnassa

Tiettyjen puiden haarat tulevat esiin joka vuosi Fibonacci -peräkkäisyyden mukaan. Ensimmäinen vuosi tavaratilassa kasvaa heittämättä mitään haaraa, vuoden kuluttua se tuottaa yhden ja niin vuosittain. Jokainen haara puolestaan ​​voi heittää uuden uuden vuoden kuluttua, aivan kuten kanit lisääntyvät.

Auringonkukkakukkikeskus sisältää molemmissa mielessä logaritmisissa spiraalisäteissä järjestetyt siemenet, joiden määrät vastaavat kahta peräkkäistä Fibonacci -numeroa.

Fibonacci -lukuja on läsnä auringonkukan ja margariittikukkien terälehden lukumäärässä, samoin kuin lukuisissa malleissa, joissa kasvit ovat lehtiä.

Voi palvella sinua: Ordinaalimuuttuja

Asiantuntijat sanovat, että tällä tavoin kasvit optimoivat lehtien ja kukien tilaa optimaaliseksi kasvulle.

Kun lähtökohta on lähtökohta, nämä rakenteet kasvavat ja vastaanottavat auringonvaloa, joten uusien lehtien ja terälehden on katettava mahdollisimman vähän ne, jotka tulivat ensin ulos. Ja paras tapa saavuttaa tämä on omaksua kasvukuvio Fibonacci -sekvenssin suhteen.

Fibonaccin peräkkäisyys eläimissä

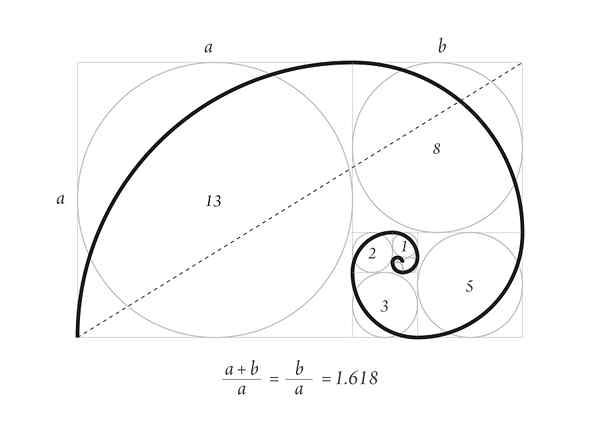Dureron spiraali Fibonaccin peräkkäisen ensimmäisen numeron kanssa

Ylemmän kuvan kestävä spiraali on osa merieläinten kuorien kasvukuviota ja joidenkin märehtijöiden sarvet.

Aloita kahdella neliöllä 1, yksi toisen päällä, sitten sen vieressä olevan sivun 2 neliö, joka muodostaa sivun 3 suorakulmion, jonka sivuilla on kultainen osuus.

Alla on sivun 3 neliö ja vasemmalle sivun 5 neliö. Yläpuolella on sivun 8 neliö ja oikealla puolella 13. Nämä ovat peräkkäin ensimmäiset numerot.

Lopuksi spiraali piirretään koskettamalla neliöiden kulmien pisteitä, kuten kuvassa nähdään.

Sovellukset

Fibonaccin peräkkäisyyttä käytetään eri aloilla:

-Artissa Fibonaccin peräkkäisyyteen liittyvä kultainen osuus esiintyy ihmisissä ja asioissa, joita edustavat suuret taiteilijat, kuten Leonardo Da Vinci, Miguel Ángel ja Alberto Durero.

-Ateenan kumppanin osuudet reagoivat myös kullanumeroon.

-Mozartin, Beethovenin, Schubertin ja Debussyn sävellyksissä.

-Suunnitella esineitä, joiden mittasuhteet näyttävät harmonisilta ihmisen silmille, kuten luottokortit, astiat, liput.

-Osakemarkkinoilla sitä käytetään ennustamaan, mitkä hinnat palauttavat sen suuntauksensa.

Viitteet

1. Fibonacci -peräkkäisyys. Toipunut: Blogeducastur.On.
2. Stewart, J. 2007. Ennakkoluulo. Viides. Painos. Cengage -oppiminen.
3. Vargas, m. Fibonacci -peräkkäissovellukset. Palautettu: Maesup.Cl.
4. Wikipedia. Fibonacci -numero. Haettu: vuonna.Wikipedia.org.