Lineaariset aallot käsite, ominaisuudet, esimerkit

Se Lineaariset aallot Nämä ovat niitä, joissa superpositioperiaatetta sovelletaan, toisin sanoen ne, joissa aaltomuoto ja sen avaruus-aika-evoluutio voidaan saavuttaa perusratkaisujen summana, esimerkiksi harmonisesta tyypistä. Kaikki aallot eivät täytä superpositioperiaatetta, joka ei noudata sitä.

"Lineaarinen" nimellisarvo johtuu siitä, että lineaariset aallot tyydyttävät aina differentiaaliyhtälön osittaisissa johdannaisissa, joissa kaikki riippuvaiset muuttujat tai sen johdannaiset liittyvät termit nostetaan ensimmäiseen voimaan.

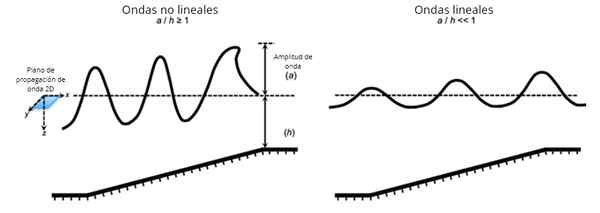
Etäisyydessä näkyvät aallot ovat lineaarisia aaltoja, mutta etualan pelotetut aallot ovat ei lineaalisia. Lähde: Pixabay.

Toisaalta, ei-lineaaliset aallot täyttävät aaltoyhtälöt, joilla on neliömäinen tai korkeampi aste riippuvaisessa muuttujassa tai johdannaisissa.

Joskus se on hämmentynyt lineaarisiin aaltoihin, joilla on pitkittäisaallot, jotka ovat ne, joissa värähtely tapahtuu samaan etenemiseen, kuten ääniaallot.

Mutta pitkittäiset aallot, samoin kuin poikittaiset, voivat puolestaan ​​olla lineaarisia tai epälineaarisia muun muassa alkuperäisen häiriön ja ympäristön amplitudista ja ympäristöstä, johon ne leviävät.

Yleensä tapahtuu, että kun alkuperäinen häiriö on pieni amplitudi, aallon etenemistä kuvaava yhtälö on lineaarista tyyppiä tai se voidaan linjata tietyillä lähestymistavoilla, vaikka se ei aina ole niin.

[TOC]

Differentiaaliyhtälö lineaarisissa aaltoissa

Lineaarisessa väliaineessa avaruuden ja ajan rajoitettu aaltomuoto voidaan edustaa eri taajuuksien ja aallonpituuksien sinus- tai kosini -aaltofunktioiden summalla Fourier -sarjan kautta. 

Lineaarisilla aaltoilla on aina liittyvä lineaarista tyyppiä erotteluyhtälö, jonka ratkaisu edustaa ennustetta siitä, mikä on häiriötä alkuperäisen häiriön takaosan hetkissä, jotka sijaitsevat alueellisesti alkuperäisessä välittömässä välittömässä.

Klassinen lineaarinen aaltoyhtälö yhdessä spatiaalisessa ulottuvuudessa, jonka ratkaisut ovat lineaarisia aaltoja, on:

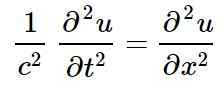
Edellisessä yhtälössä tai edustaa tietyn fyysisen määrän häiriötä asennossa x Ja tällä hetkellä t, tarkoittaen tai Se on funktio x ja t-

Se voi palvella sinua: Mitkä ovat koplanaresvektorit? (Ratkaistujen harjoitusten kanssa)

u = u (x, t)

Esimerkiksi, jos se on ääniaalto ilmassa, tai Se voi edustaa paineen vaihtelua sen arvon suhteen häiritsemättä.

Sähkömagneettisen aallon tapauksessa tai edustaa sähkökenttää tai magneettikenttää värähtelemään kohtisuorassa etenemissuuntaan nähden.

Ketterin köyden tapauksessa, tai edustaa ristin siirtymistä suhteessa köyden tasapainon tasapainoon, kuten seuraavassa kuvassa on esitetty:

Aaltomuoto tietyssä hetkessä, lineaaristen aaltojen tapauksessa tämä muoto on eri taajuuden ja aallonpituuksien sinimuotoisten aaltojen päällekkäisyys. Lähde: f. Zapata.

Differentiaaliverkkolatkaisut

Jos sinulla on kaksi tai useampaa lineaarisen differentiaaliyhtälön ratkaisua, jokainen liuos kerrottuna vakiona on ratkaisu ja on myös summa niiden summa. 

Toisin kuin epälineaariset yhtälöt, Waveline-yhtälöt myöntävät tyypin harmoniset ratkaisut: 

tai₁= A⋅sen (k⋅x - ωolem) ja tai₂= A⋅sen (k⋅x + ωolem) 

Tämä voidaan varmistaa yksinkertaisella korvaamisella lineaarisessa aaltoyhtälössä.

Ensimmäinen ratkaisu edustaa progressiivista aaltoa, joka etenee oikealle, kun taas toinen vasemmalle C = ω/k.

Harmoniset ratkaisut ovat ominaisia ​​lineaarisille aaltoyhtälöille.

Toisaalta kahden harmonisen liuoksen lineaarinen yhdistelmä on myös ratkaisu esimerkiksi lineaariseen aaltoyhtälöön:

u = a₁ cos (k₁⋅x - ω₁⋅T) + a₂ synti (k₂⋅x - ω₂⋅T) on liuos.

Lineaaristen aaltojen merkityksellisin ominaisuus on, että mikä tahansa aalto, riippumatta monimutkainen, voidaan saada rintojen ja kosiinin yksinkertaisten harmonisten aaltojen summalla:

u (x, t) = a_{0 -} + ∑_n -Lla_n cos (k_n⋅x - ω_n⋅T) + ∑_m B -_m synti (k_m⋅x - ω_m⋅T).

Dispergoivat ja ei -dispergoivat lineaariset aallot

Klassisessa lineaarisessa aaltoyhtälössä, c edustaa pulssin etenemisen nopeutta.

Ei -dispergoivat aallot

Tapauksissa, joissa c Se on vakioarvo, esimerkiksi sähkömagneettiset aallot tyhjyydessä, sitten pulssi alkuperäisessä hetkessä t = 0 Muoto f (x) Se leviää:

u (x, t) = f (x - c⋅t)

Kärsimättä vääristymistä. Kun näin tapahtuu, sanotaan, että väliaine ei ole suunniteltu.

Dispergoivat aallot

Dispergoivassa väliaineessa etenemisnopeus voi kuitenkin riippua aallonpituudesta λ, toisin sanoen: c = c (λ).

Voi palvella sinua: Jatkuvuusyhtälö

Sähkömagneettiset aallot ovat dispergoivia, kun matkustat materiaalin väliaineen läpi. Myös veden pinta -aallot kulkevat eri nopeudella veden syvyyden mukaan.

Nopeus, jolla harmoninen aalto etenee A⋅sen (k⋅x - ωolem) On Ω/k = c ja vaiheen nopeutta kutsutaan. Jos väliaine on dispergoiva, niin niin c Se on aaltolukutoiminto k -k -- C = c (k), missä k -k - Se liittyy aallonpituuteen K = 2π/λ.

Hajautussuhteet

Taajuuden ja aallonpituuden välistä suhdetta kutsutaan hajontasuhde, joka ilmaisi kulmataajuuden suhteen Ω ja aallonumero k -k - On: Ω = c (k) ⋅k.

Jotkut lineaaristen aaltojen dispersiosuhteiden ominaisuudet ovat seuraavat:

Aaltoissa, joissa aallonpituus (harjanteiden välinen etäisyys) on paljon suurempi kuin syvyys H, Mutta se, että sen leveys on paljon pienempi kuin dispersio -suhde on:

Ω = √ (gh) ⋅k

Sieltä päätellään, että ne leviävät vakiona nopeudella √ (GH) (ei -dispergoiva puoli).

Mutta erittäin syvien vesien aallot ovat dispergoivia, koska niiden leviämissuhde on:

ω = √ (g/k) ⋅K

Tämä tarkoittaa sitä vaiheitaa Ω/k Se on muuttuva ja riippuu aallonumerosta ja siten aallon aallonpituudesta.

Ryhmänopeus

Jos kaksi harmonista lineaarista aaltoa ovat päällekkäisiä, mutta etenevät eri nopeuksilla, niin ryhmänopeus (toisin sanoen aaltopaketin) ei vastaa vaiheitaa.

Ryhmänopeus v_g Se määritellään taajuusjohdannaiseksi dispersio -suhteen aallonumeron suhteen: v_g = Ω '(k).

Seuraava kuva näyttää kahden harmonisen aallon päällekkäisyyden tai summan tai₁= A⋅sen (k₁⋅x - ω₁⋅T) ja tai₂= A⋅sen (k₂⋅x - ω₂⋅T) jotka kulkevat eri nopeudella v₁= Ω₁/k₁ ja v₂= Ω₂/k₂. Huomaa, kuinka ryhmänopeus eroaa vaiheen nopeudesta, tässä tapauksessa ryhmänopeus on ∆ω/∆k.

Se voi palvella sinua: materiaalien magneettiset ominaisuudet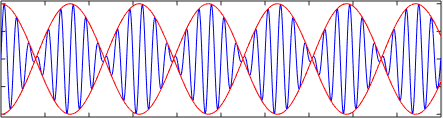Lineaarinen (sininen) aalto dispergoivassa väliaineessa. Punainen käyrä on lisätty korostamaan, että ryhmän nopeus on erilainen kuin etenemisnopeus

Dispersio -suhteesta riippuen vaiheen nopeus ja ryhmänopeus vastakkaisiin suuntiin voivat olla jopa vastakkaisia ​​suuntoja.

Esimerkkejä lineaarisista aaltoista

Elektromagneettiset aallot

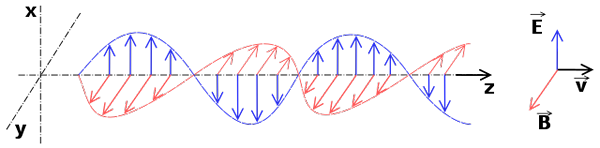Sähkömagneettiset aallot, jotka muodostavat sähkömagneettisen säteilyn

Sähkömagneettiset aallot ovat lineaarisia aaltoja. Sen aaltoyhtälö johdetaan myös lineaarisen sähkömagneettisuuden (Maxwell -yhtälöiden) yhtälöistä.

Schrödingerin yhtälö

Se on yhtälö, joka kuvaa hiukkasten dynamiikkaa atomi -asteikolla, jossa aaltoilevat ominaisuudet ovat merkityksellisiä, esimerkiksi atomin elektronien tapaus.

Sitten "elektroniaalto" tai aaltofunktio, kuten sitä kutsutaan, on lineaarinen aalto.

Aaltoja syvässä vedessä

Lineaariset aallot ovat myös niitä, joissa amplitudi on paljon pienempi kuin aallonpituus ja aallonpituus paljon suurempi kuin syvyys. Syvän veden aallot seuraavat lineaarista teoriaa (tunnetaan nimellä Airyn aaltoileva teoria).

Aalto, joka lähestyy rantaa ja muodostaa kuitenkin valssatun (ja surffaajat rakastavat) ominaisen harjanteen on epälineaarinen aalto.

Ääni

Koska ääni on pieni ilmakehän paineen häiriö, sitä pidetään lineaarisena aaltona. Supersonic -tason räjähdyksen tai aaltoferen iskun aalto ovat kuitenkin tyypillisiä epälineaarisia aalto -esimerkkejä.

Aallot kireällä köydellä

Jännitetyn köyden läpi leviävät aallot ovat lineaarisia, edellyttäen, että alkuperäinen pulsaatio on pieni, toisin sanoen köyden elastisen rajan ei ylitä.

Jousien lineaariset aallot heijastuvat niiden päissä ja päällekkäisyyksissä, jolloin saadaan paikallaan olevat aallot tai värähtelytilat, jotka antavat merkkijonoinstrumenttien ominaisia ​​harmonisia ja subarmonisia sävyjä.

Viitteet

1. Griffiths G ja Schiesser W. Lineaariset ja epälineaariset aallot. Toipunut: Sholarpedia.org.
2. Whitham g.B -. (1999) "Lineaariset ja epälineaariset aallot". Viiva. 
3. Wikipedia. Epälineaariset aallot. Palautettu: on.Wikipedia.com
4. Wikipedia. Epälineaarinen akustinen. Haettu: vuonna.Wikipedia.com
5. Wikipedia. Aalto. Haettu: vuonna.Wikipedia.com
6. Wikiwaves. Epälineaariset aallot. Toipunut: wikiwaves.org