Sarja voimaesimerkkejä ja harjoituksia

Eräs Power -sarja Se koostuu termien summasta muuttujan voimien muodossa x, tai yleisemmin, X-C, missä c Se on jatkuva reaaliluku. Summan summan summan summalla se ilmaistaan ​​seuraavasti:

∑a_n (X -c)ⁿ = a_jompikumpi + -lla₁ (x - c) + a₂ (X - c)² + -lla₃ (X - c)³ +… + A_n (X - c)ⁿ

Missä kertoimet_jompikumpi, -lla₁, -lla₂… Ne ovat todellisia numeroita ja sarja alkaa kohdasta n = 0.

Kuvio 1. Power -sarjan määritelmä. Lähde: f. Zapata.

Tämä sarja keskittyy arvoon c se on vakio, mutta voit valita sen c Olla yhtä suuri kuin 0, jolloin valtuudet yksinkertaistetaan:

∑a_n xⁿ = a_jompikumpi + -lla₁ x + a₂ x² + -lla₃ x³ +… + A_n xⁿ

Sarja alkaa -lla_jompikumpi(X-C)^{0 -} ja -lla_jompikumpix^{0 -} vastaavasti. Mutta tiedämme sen:

(X-C)^{0 -}= x^{0 -} = 1

Siksi -lla_jompikumpi(X-C)^{0 -} = -lla_jompikumpix^{0 -} = -lla_jompikumpi (Riippumaton termi)

Hyvä asia voimien voimissa on, että heidän kanssaan voit ilmaista toimintoja ja tällä on monia etuja, varsinkin jos haluat työskennellä monimutkaisen toiminnon kanssa.

Kun näin on, sen sijaan.

Tietysti kaikki on ehdollinen sarjan lähentymiselle. Sarja lähenee, kun lisäämällä tietyn määrän termejä, saadaan kiinteä arvo. Ja jos lisäämme lisää termejä, saamme edelleen tämän arvon.

[TOC]

Toimii voimien voimina

Esimerkkinä funktiosta, joka ilmaistaan ​​valonsarjana, otetaan f (x) = e^x.

Tämä funktio voidaan ilmaista valtuuksien suhteen seuraavasti:

ja^x  ≈ 1 + x + (x² / 2!) + (X³ / 3!) + (x⁴ / 4!) + (x⁵ / 5!) +..

Missä! = n. (N-1). (N-2). (N-3)… ja se otetaan 0! = 1.

Aiomme tarkistaa laskimen avulla, mikä sarja on tehokkaasti samaan aikaan nimenomaisesti annettu toiminto. Esimerkiksi aloitetaan x = 0.

Voi palvella sinua: teoreettinen todennäköisyys: Kuinka saada se ulos, esimerkkejä, harjoituksia

Tiedämme, että e^{0 -} = 1. Katsotaanpa mitä sarja tekee:

ja^{0 -} ≈ 1 + 0 + (0² / 2!) + (0³ / 3!) + (0⁴ / 4!) + (0⁵ / 5!) +… = 1

Ja nyt yritetään x = 1. Laskin heittää sen ja¹ = 2.71828, Ja sitten verrataan sarjaan:

ja¹ ≈ 1 + 1 + (1² / 2!) + (1³ / 3!) + (1⁴ / 4!) + (1⁵ / 5!) +… = 2 + 0.5000 + 0.1667 + 0.0417 + 0.0083 +… ≈ 2.7167

Vain viidellä termillä meillä on jo tarkka sattuma vuonna e ≈ 2.71. Sarjamme puuttuu vain vähän enemmän, mutta kun lisätään enemmän termejä, kaikki varmuudella sarja lähenee tarkkaa arvoa ja. Esitys on tarkka milloin N → ∞.

Jos edellinen analyysi toistetaan n = 2 Saadaan hyvin samanlaisia ​​tuloksia.

Tällä tavalla olemme varmoja, että eksponentiaalinen funktio f (x) = e^x Sitä voi edustaa tämä valtuudet:

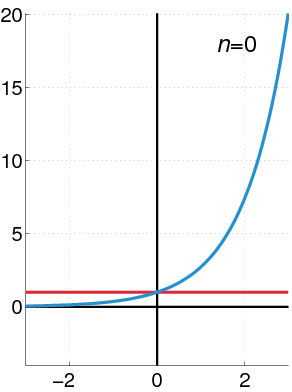Kuva 2. Tässä animaatiossa sitä nähdään, koska valtuudet ovat lähempänä eksponentiaalista toimintoa, koska enemmän termejä otetaan. Lähde: Wikimedia Commons.

Voimien geometriset voimat

Toiminto f (x) = e^x Se ei ole ainoa toiminto, joka myöntää valtuuksien sarjan esityksen. Esimerkiksi toiminto  F(x) = 1/1 - x  Se näyttää paljon kuin tunnettu Konvergenssi geometrinen sarja-

∑a.r -ⁿ = A / 1 - r

Tee vain a = 1 ja r = x saadaksesi sopivan sarjan tähän toimintoon, joka on keskittynyt C = 0: n:

On kuitenkin tiedossa, että tämä sarja on konvergenssi │r│: lle<1, por lo tanto la representación es válida únicamente en el intervalo (-1,1), aunque la función sea válida para todo x, excepto x=1.

Kun haluat määritellä tämän toiminnon toisella aikavälillä, se keskittyy yksinkertaisesti riittävään arvoon ja valmiina.

Kuinka löytää funktion voimien sarjan kehitys

Mikä tahansa funktio voidaan kehittää C: hen keskittyneissä voimasarjoissa, kunhan olet johdettu kaikista x = c: n tilauksista. Menettelyssä käytetään seuraavaa lausetta, nimeltään Taylor -lause:

Olkoon f (x) funktio tilausjohdannaisilla n, merkitty F^(N), joka myöntää valtuuksien sarjan kehittämisen aikavälillä Yllyttää. Sen kehitys Taylor -sarja On:

Se voi palvella sinua: mikä on kokonaisten ja desimaalien sijainti?

Jotta:

f (x) = f (c) + f '(c) (x-c) + f "(c) (x-c)² /2 + f "(c) (x-c)³ /6 +… r_n

Missä r_n, joka on sarjan n., Sitä kutsutaan jäännös-

Kun c = 0, sarjaa kutsutaan Maclaurin -sarja.

Tämä tässä annettu sarja on identtinen alussa annetun sarjan kanssa, vasta nyt on tapa löytää nimenomaisesti kunkin termin kertoimet, jotka ovat antaneet:

On kuitenkin varmistettava, että sarja välittää toiminnon, jonka haluat edustaa. Se tapahtuu, että kaikki Taylor -sarjat eivät välttämättä lähene F (x): tä, joka oli mielessä kertoimien laskiessa -lla_n.

Tämä tapahtuu, koska ehkä toiminnasta johdetut, arvioidut x = c samaan aikaan kuin toisesta johdettujen saman arvon kanssa, myös x = c. Tässä tapauksessa kertoimet olisivat samat, mutta kehitys olisi epäselvä, koska sillä ei ole varmuutta, jonka toiminto vastaa.

Onneksi on tapa tietää:

Lähentymiskriteerit

Epäselvyyden välttämiseksi, jos r_n → 0 Kun N → ∞ kaikille x: lle aikavälillä I, sarja lähenee F (x).

Harjoittele

- Liikunta ratkaistiin 1

Etsi funktion geometriset voimat f (x) = 1/2 - x keskittynyt C = 0: een.

Ratkaisu

Annettu funktio on ilmaistava tavalla, joka vastaa niin paljon kuin mahdollista 1 /1-x: llä, jonka sarja tunnetaan. Siksi kirjoitamme numeraattorin ja nimittäjän muuttamatta alkuperäistä ilmaisua:

1/2 - x = (1/2) / [1 - (x / 2)]

Koska ½ on vakio, se menee summasta, ja tämä on kirjoitettu uuden muuttujan x/2 perusteella:

Voi palvella sinua: Konjugoidut binomial: miten se on ratkaistu, esimerkkejä, harjoituksia

Huomaa, että x = 2 ei kuulu funktion alueelle ja osiossa annettujen lähentymiskriteerien mukaan Voiman geometrinen sarja, Kehitys on voimassa │x/2│: lle< 1 o equivalentemente -2 < x < 2.

- Liikunta ratkaistiin 2

Löydä MacLaurinin funktion F (x) = Sen X -sarjan 5 ensimmäiset termit.

Ratkaisu

Vaihe 1

Ensinnäkin ovat johdannaiset:

-Johdettu järjestyksestä 0: Se on sama funktio f (x) = sen x

-Ensimmäinen johdannainen: (sin x) '= cos x

-Toinen johdannainen: (sin x) "= (cos x) '= - sin x

-Kolmas johdannainen: (sin x) "= (-sen x) '= - cos x

-Neljäs johdannainen: (sin x) "= (- cos x) '= sin x

Vaihe 2

Sitten jokainen johdannainen arvioidaan x = C: ssä, samoin kuin maclauriinin kehitys, c = 0:

synti 0 = 0; cos 0 = 1; - Sen 0 = 0; -Cos 0 = -1; synti 0 = 0

Vaihe 3

Kertoimet on rakennettu_n;

-lla_jompikumpi = 0/0! = 0; -lla₁ = 1/1! = 1; -lla₂ = 0 /2! = 0; -lla₃ = -1 / 3!; -lla₄ = 0/4! = 0

Vaihe 4

Lopuksi sarja on koottu:

sin x ≈ 0.x^{0 -} + 1. x¹ + 0 - .x² - (1/3!) x³ + 0 -.x⁴... = x - (1/3!) x x³  +..

Tarvitseeko lukija lisää termejä? Kuinka monta muuta sarja on lähempänä toimintoa.

Huomaa, että kertoimissa on kuvio, seuraava ei -nolla termi on₅ Ja kaikki pariton hakemisto eroavat myös 0: sta, vuorotellen merkkejä, niin että:

Sen x ≈ x - (1/3!) x x³  + (1/5!) x x⁵ - (1/7!) x x⁷  +.. .

Se on jätetty harjoitukseksi tarkistaa, voit käyttää osamäärän suhde Sarjan lähentymiseen.

Viitteet

1. CK-12-säätiö. Power -sarja: toimintojen ja toimintojen esitys. Toipunut: CK12.org.
2. Engler, a. 2019. Kiinteä laskenta. Rannikon kansallinen yliopisto.
3. Larson, r. 2010. Muuttujan laskenta. 9NA. Painos. McGraw Hill.
4. Ilmaiset matematiikan tekstit. Power -sarja. Toipunut: matematiikka.Libretext.org.
5. Wikipedia. Power -sarja. Palautettu: on.Wikipedia.org.