Vallankumouksen kiinteiden aineiden tilavuus, tyypit, ratkaistut harjoitukset

Hän Vallankumous Se on kolmiulotteinen kuva, joka syntyy litteän pinnan kiertämällä aksiaalitakselin tai vallankumouksen akselin ympärillä. Kuvio 1 esittää tällä tavalla syntyvän vallankumouksen kiinteän animaation.

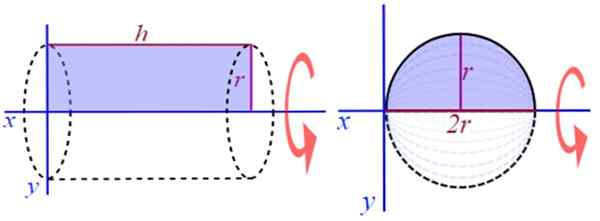
Toinen erittäin helppo esimerkki visualisoinnista on luoda suora pyöreä sylinteri, pyöriä korkeuden suorakulmio tai pitkä H ja radio R, positiivisen X -akselin ympärillä (kuva 2). Sen tilavuuden löytämiseksi on tunnettu kaava:

V = pohjapinta -ala x korkeus

Kuvio 1. Sen X -käyrän kiertämällä syntyvä kuva. Lähde: Wikimedia Commons. Macks/CC BY-SA (https: // creativecommons.Org/lisenssit/by-SA/2.5).

Muita vallankumouksen kiinteitä aineita ovat pallo, suora pyöreä kartio ja erilaiset kuviot kiertämisen pinnan mukaan ja tietysti valittu akseli.

Kuva 2. Suora pyöreän sylinterin ja pallon muodostuminen. Lähde: Wikimedia Commons.

Esimerkiksi, puolipyörän kiertäminen linjan ympärillä, joka on yhdensuuntainen halkaisijan kanssa, saadaan onton vallankumouksen kiinteä aine.

Sylinterissä, kartiossa, pallo, sekä massifit että reikät, on olemassa kaavoja, jotka löytyvät tilavuudesta, joka riippuu säteestä ja korkeudesta. Mutta muiden pintojen tuottaessa tilavuus lasketaan määriteltyjen integraalien avulla.

[TOC]

Vallankumouksen tyypit

Vallankumouksen kiinteät aineet voidaan luokitella niiden tuottavan käyrän mukaan:

Pallo

Se riittää kiertämään puolipyöreä akselin ympärille, joka on radion R -pallon halkaisija. Sen tilavuus on:

V_pallo = (4/3) πr³

Pillu

H: n ja radion r -kartion saamiseksi pinta, jonka täytyy. Sen tilavuus on:

V_Pillu = (1/3) πhr²

Sylinteri

Suorakulmion kiertäminen aksiaaliakselin ympärillä, joka kulkee yhden sivun läpi, joka voi olla lyhyt sivu tai pitkä sivu, saadaan suora pyöreä sylinteri, jonka säde R ja korkeus H, jonka tilavuus on:

Voi palvella sinua: köysi (geometria): pituus, lause ja harjoitukset

V_sylinteri = πr²H

Toroidi

Härkällä on munkin muoto. Se saadaan kiertämällä pyöreää aluetta tasossa olevan viivan ympärillä, joka ei leikkaa ympyrää. Sen tilavuus on annettu:

V_Toroidi = 2πa²R -

Missä a on poikkileikkauksen säde ja r on toroidin säde kuvassa esitetyn kaavion mukaisesti:

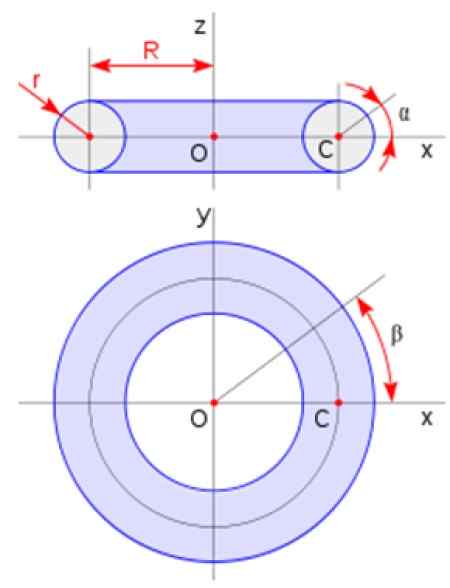Kuva 3. Toroidimitat. Lähde: Wikimedia Commons.

Menetelmät vallankumouksen määrän laskemiseksi

Integraalilaskelmassa nämä kaksi menetelmää ovat usein:

-Levyt ja aluslevyt

-Kuoret

Levymenetelmä tai aluslevyt

Kun viipaloi vallankumouksen kiinteä, poikkileikkaus voi olla albumi, jos kiinteä on kiinteä tai se voi olla eräänlainen pesukone (albumi, jolla on reikä keskellä), jos se on kiinteä reikä.

Oletetaan, että vaakasuoran akselin ympäri pyöritetään tasainen alue. Tuota litteästä alueelta otamme pienen ΔX -leveyden suorakulmion, jota pyöritetään kohtisuorassa aksiaaliakselin ympärillä.

Suorakulmion korkeus on uloimman käyrän r (x) ja eniten sisäisen R (x) välillä. Ne vastaavat vastaavasti ulkoista sädettä ja sisäistä radiota.

Tätä kiertoa tehdessäsi muodostuu AV -tilavuuden aluslevy, jonka annetaan:

ΔV = koko tilavuus - reikän tilavuus (jos sellainen on)

Muistaen, että suoran pyöreän sylinterin tilavuus on π. radio² x Korkeus, meillä on:

Δv = π [r²(x) - r²(x)] Δx

Kiinteä aine voidaan jakaa moniin pieniin tilavuuden ΔV osiin. Jos lisäämme ne kaikki, meillä on koko tilavuus.

Tätä varten meillä on taipumus 0 tilavuuteen ΔV, josta tulee myös hyvin pieni, ja siitä tulee dx -ero.

Se voi palvella sinua: molemminpuolisesti epäyhtenäisiä tapahtumia: Ominaisuudet ja esimerkit

Siksi meillä on olennainen:

V = ∫_-lla^{b -} π [r²(x) - r²(x)] dx

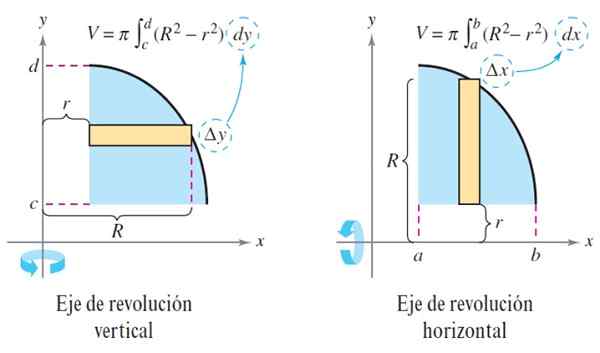Kuva 3. Aluslevymenetelmä. Lähde: Larson. R -. Laskeminen.

Siinä tapauksessa, että kiinteä aine on kiinteä, sitten funktio r (x) = 0, muodostetun kiinteän aineen viipale on levy ja tilavuus pysyy:

V = ∫_-lla^{b -} πr²(x) dx

Kun vallankumouksen akseli on pystysuora, aiemmat yhtälöt ovat muodossa:

V = ∫_-lla^{b -} π [r² (Y) - r² (y)] dy ja v = ∫_-lla^{b -} πr²(Y) dy

Kerros

Kuten nimi huomauttaa, tämä menetelmä on olettaa, että kiinteä aine koostuu differentiaalisista paksuista kerroksista. Kerros on ohut putki, joka on peräisin suorakulmion käännöksestä pyörimisakselin kanssa.

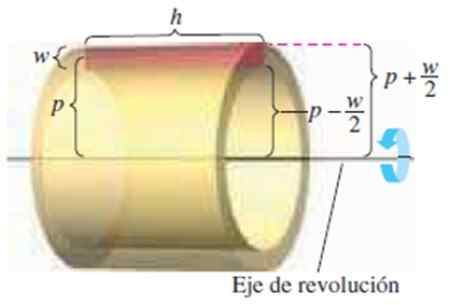Kuva 4. Lieriömäinen korkeus 2, pitkä H ja säde p. Lähde: Larson, R. Laskeminen.

Meillä on seuraavat mitat:

-Suorakulmion korkeus W -

-Sen pituusaste h

-Etäisyys suorakulmion keskustasta kierto -akseliin p

Tietäen, että kerroksen tilavuus on Ulkotila - sisustustilavuus-

π (p + w/2)²H - π (p - w/2)²h

Kehitettäessä merkittäviä tuotteita ja yksinkertaistamista, se saadaan:

Kerroksen tilavuus = 2π⋅p⋅w⋅h

Tehdään nyt suorakulmion korkeus W, kuten seuraavassa kuvassa nähdään:

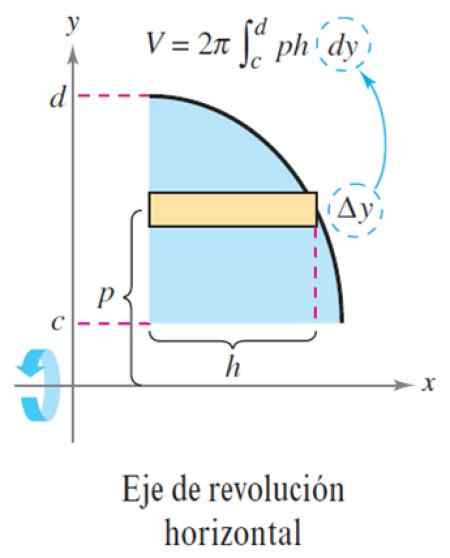Kuva 5. Vaakasuuntainen vallankumouksen akselikerrosmenetelmä. Lähde: Larson, R. Muuttujan laskenta.

Tämän kanssa tilavuus ΔV on:

Δv = 2π p x h x Δy

Ja kerrosten määrän tekeminen n Ole erittäin suuri, AY: stä tulee differentiaalinen DY, joten kokonaistilavuus on olennainen:

V = ∫_c^{d -d} 2π p (y) h (y) dy

Kuvattua menettelyä sovelletaan samalla tavalla, kun vallankumousakseli on pystysuora:

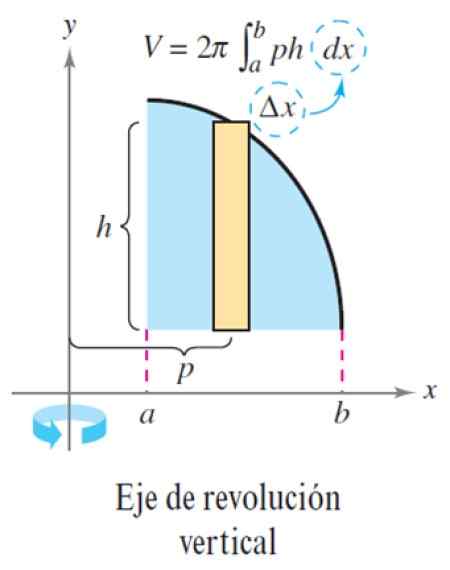Kuva 6. Kerrosmenetelmä pystysuoraan vallankumousakseliin. Lähde: Larson, R. Muuttujan laskenta.

Liikuntaa

Löydä äänenvoimakkuus, joka syntyy käyrien välisen tasaisen alueen pyörimisellä:

y = x²;  y = 0; x = 2

Akselin ympärillä ja.

Voi palvella sinua: negatiivinen homotecia

Ratkaisu

-Ensimmäinen tehtävä on kuvaaja alue, joka tuottaa vallankumouksen kiinteän ja osoittaa kääntöakselin. Meillä on se seuraavassa kaaviossa:

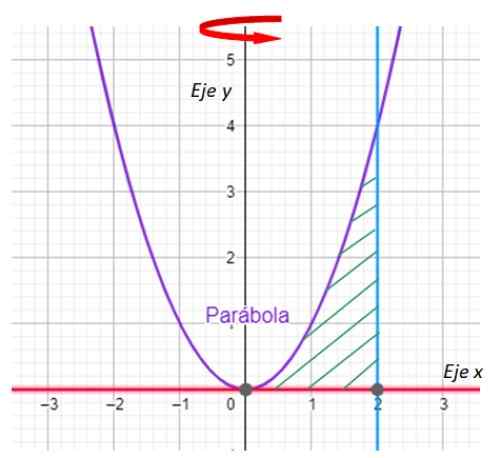Kuva 7. Harjoituksen käyrien kaavio ratkaistu. Lähde: f. Zapata geogebralla.

-Nyt etsitään käyrän y = x välisiä risteyksiä² ja rivi x = 2. Sen puolesta linja y = 0 ei ole kukaan muu kuin x -akseli.

On helppo varoittaa, että vertaus ja viiva leikkaavat pisteessä (2,4), joka vahvistetaan korvaamalla x = 2 y = x: lla².

-Sitten valitaan yksi tilavuuden laskemismenetelmistä, esimerkiksi kerrosmenetelmä pystysuoralla vallankumousakselilla:

V = ∫_-lla^{b -} 2π p (x) h (x) dx

Vaihe 1: Piirrä suorakulmio

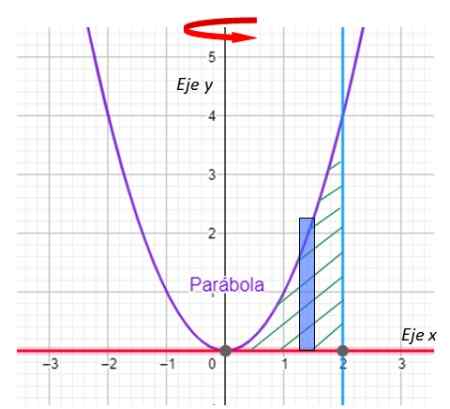Kuva 8. Suorakulmio ratkaistu esimerkki. Lähde: f. Zapata geogebralla.

Tärkeä: Kerrosmenetelmässä suorakulmion pitkä puoli on yhdensuuntainen kierto -akselin kanssa.

Vaihe 2: Määritä p (x)

Kerroksen kerros on x

Vaihe 3: Määritä H (x)

Suorakulmion korkeus määritetään vertauksella x².

Vaihe 4: Luo ja ratkaise äänenvoimakkuuden integraali

Integraatiomuuttuja on x, joka vaihtelee välillä 0 - 2, tällä on integraatiorajat. P (x): n ja H (x): n lausekkeiden korvaaminen

 Jotkut harjoitukset voidaan ratkaista molemmilla menetelmillä. Voiko lukija ratkaista tämän aluslevymenetelmällä?

Viitteet

1. Larson, r. 2010. Muuttujan laskenta. 9NA. Painos. McGraw Hill.
2. Purcell, E. 2007. Laskenta analyyttisellä geometrialla. 9NA. Painos. Pearson -koulutus.
3. Wikipedia. Vallankumous. Haettu: vuonna.Wikipedia.org.
4. Wikipedia. Toroidi. Palautettu: on.Wikipedia.org.
5. Wolfram Mathworld. Vallankumous. Toipunut: MathWorld.Susi.com.