Neliömäiset peräkkäiset esimerkit, sääntö ja harjoitukset ratkaistu

Se Kvadraattiset peräkkäit, Matemaattisesti ne koostuvat tietyn aritmeettisen säännön seuraavista numeroiden sekvensseistä. On mielenkiintoista tietää tämä sääntö minkä tahansa peräkkäisen ehtojen määrittämiseksi.

Yksi tapa saavuttaa tämä on määrittää ero kahden peräkkäisen termin välillä ja nähdä, onko saatu arvo aina toistettu. Kun niin, sanotaan, että se on säännöllinen peräkkäisyys.

Numeeriset peräkkäit ovat tapa järjestää numerosekvenssejä. Lähde: Pixabay.com

Mutta jos sitä ei toisteta, voit yrittää tutkia Ero erojen välillä Ja katso onko tämä arvo vakiona. Jos niin, niin se on a Neliömäinen peräkkäisyys. 

[TOC]

Esimerkkejä säännöllisistä peräkkäisistä ja neliömäisistä peräkkäisistä

Seuraavat esimerkit auttavat selventämään, mitä on tähän mennessä selitetty:

Esimerkki säännöllisestä peräkkäisestä

Olla peräkkäin S = 4, 7, 10, 13, 16, ...

Tämä peräkkäisyys, jonka S: n merkitsee, on ääretön numeerinen joukko tässä tapauksessa kokonaisluku.

Voidaan nähdä, että se on säännöllinen peräkkäinen, koska jokainen termi saadaan lisäämällä 3 edelliseen termiin tai elementtiin:

4

4 +3 = 7

7+3 = 10

10+3 = 13

13+3 = 16

Toisin sanoen: Tämä peräkkäisyys on säännöllinen, koska ero seuraavan termin ja edellisen välillä antaa kiinteän arvon. Tämän arvon mukaan annetussa esimerkissä on 3.

Säännöllisiä peräkkäin, jotka saadaan lisäämällä kiinteän määrän edelliseen termiin, kutsutaan myös aritmeettinen eteneminen. Ja eroavaksi - vakiona - peräkkäisten termien joukossa syy Ja se on merkitty nimellä r.

Esimerkki ei -säännöllisestä ja neliömäisestä peräkkäisestä

Katso nyt seuraava peräkkäin:

S = 2, 6, 12, 20, 30, .. .

Kun peräkkäiset erot lasketaan, saadaan seuraavat arvot:

Voi palvella sinua: Satunnaiset valinnat korvaavan tai ilman

6-2 = 4

12-6 = 6

20-12 = 8

30-20 = 10

Niiden erot eivät ole vakioita, joten voidaan sanoa, että se on ei -säännöllinen peräkkäin.

Kuitenkin, jos tarkastellaan eroja, on toinen peräkkäinen, joka merkitään nimellä S_Dif-

S_Dif = 4, 6, 8, 10, .. .

Tämä uusi peräkkäisyys on a säännöllinen peräkkäisyys, Koska jokainen termi saadaan lisäämällä kiinteä arvo r = 2 edelliseen. Siksi voimme vahvistaa, että S on Neliömäinen peräkkäisyys.

Yleinen sääntö neliömäisen peräkkäisyyden rakentamiseksi

Neliöllisen peräkkäisyyden rakentamiseksi on yleinen kaava:

T_n = A ∙ n² + B ∙ n +c

Tässä kaavassa t_n Se on peräkkäisen nime. A, B ja C ovat kiinteitä arvoja, kun taas N vaihtelee yksi kerrallaan, eli 1, 2, 3, 4, ..

Edellisen esimerkin peräkkäin S A = 1, B = 1 ja C = 0. Sieltä seuraa, että kaava, joka tuottaa kaikki termit, on: t_n = n² + n

Tarkoittaen:

T₁ = 1² + 1 = 2

T₂ = 2² + 2 = 6

T₃ = 3² + 3 = 12

T₅ = 5² + 5 = 30

T_n = n² + n

Ero kahden peräkkäisen neliön peräkkäisen termin välillä

T_N+1 - T_n = [A ∙ (n+1)² + B ∙ (n + 1) + c] - [a ∙ n² + B ∙ n +c]

Ilmaisun kehittäminen merkittävän tuotteen avulla on edelleen:

T_N+1 - T_n = A ∙ n² + A ∙ 2 ∙ n + a + b ∙ n + b + c - a ∙ n² - B ∙ n - c

Yksinkertaistamalla sitä saat:

T_N+1 - T_n = 2 ∙ a ∙ n + a + b

Tämä on kaava, joka antaa erojen peräkkäisyyden S_Dif Se voidaan kirjoittaa näin:

Dif_n = A ∙ (2n+1)+b

Missä selvästi seuraava termi on 2 ∙ Joskus edellinen. Eli syy erojen peräkkäisyyteen S_Dif ES: r = 2 ∙ a.

Ratkaisivat kvadraattiset peräkkäin harjoitukset

Harjoitus 1

Olla peräkkäin S = 1, 3, 7, 13, 21,…. Määritä kyllä:

i) se on säännöllistä tai ei

ii) on neliöllinen vai ei

iii) oli neliöllinen, erojen peräkkäisyys ja niiden syy

Se voi palvella sinua: Rajoita ominaisuuksia (esimerkkien kanssa)

Vastaukset

i) Lasketaan ero seuraava termi ja edellinen:

3-1 = 2

7-3 = 4

13-7 = 6

21-13 = 8

Voimme vakuuttaa, että peräkkäisyys S ei ole säännöllinen, koska ero peräkkäisten termien välillä ei ole vakio.

ii) Erojen peräkkäisyys on säännöllinen, koska sen termien välinen ero on vakioarvo 2. Siksi alkuperäinen peräkkäisyys on neliöllinen.

iii) Olemme jo päättäneet, että S on neliöllinen, erojen peräkkäisyys on:

S_Dif = 2, 4, 6, 8,… ja sen syy on r = 2.

Harjoitus 2

Olla edellisen esimerkin peräkkäisyys s = 1, 3, 7, 13, 21,…, missä se varmistettiin, että se on neliömäinen. Päättää:

i) kaava, joka määrää yleisen termin t_{n .}

ii) Vahvista kolmas ja viides termi.

iii) Kymmenennen termin arvo.

Vastaukset

i) T: n yleinen kaava_n on ∙ n² + B ∙ n +c. Sitten tiedetään A, B ja C arvot.

Erojen peräkkäisyys on oikein 2. Kaikkien kvadraattisten peräkkäisyyksien lisäksi syy R on 2 ∙ A, kuten edellisissä osissa osoitetaan.

R = 2 ∙ A = 2, joka saa meidät päättämään, että a = 1.

Erojen ensimmäinen termi s_Dif Se on 2 ja sen on noudatettava ∙ (2n+1)+b, n = 1 ja a = 1, eli:

2 = 1 ∙ (2 ∙ 1+1)+B

Selvä B saadaan: b = -1

Sitten S (n = 1) Vale 1 -termi (n = 1), eli 1 = a ∙ 1² + B ∙ 1 + C. Kuten jo tiedämme, että a = 1 ja b = -1 korvataan meidät, olemme jäljellä:

1 = 1 ∙ 1² + (-1) ∙ 1 +C

C -selvitys saadaan arvonsa: C = 1.

Yhteenvetona:

A = 1, b = -1 ja c = 1

Sitten termi on vain_n = n² - N + 1

ii) Kolmas termi t₃ = 3² - 3 + 1 = 7 ja vahvistetaan. Viides t₅ = 5² - 5 + 1 = 21, joka on myös varmennettu.

iii) Kymmenes termi on t₁₀ = 10² - 10 + 1 = 91.

Harjoitus 3

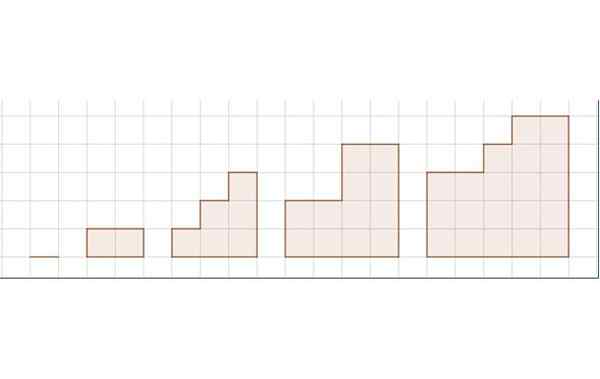Harjoituksen 3 alueiden sekvenssi. Lähde: Itse tehty.

Kuvio näyttää viiden luvun sekvenssin. Retikulaari edustaa pituuden yksikköä.

Voi palvella sinua: ero yhteisen osan ja desimaalin välillä

i) Määritä luvualueen peräkkäisyys.

i) Osoita, että se on neliöllinen peräkkäin.

iii) Löydä kuvan # 10 alue (ei esitetty).

Vastaukset

i) Kuvioiden sekvenssin aluetta vastaava peräkkäisyys on:

S = 0, 2, 6, 12, 20,…

ii) S: n peräkkäisiä eroja vastaava peräkkäin on:

S_Dif = 2, 4, 6, 8,…

Koska peräkkäisten termien väliset erot eivät ole vakioita, joten s ei ole säännöllinen peräkkäin. Sen on tiedettävä, onko se neliöllinen, jolle teemme jälleen erojen sekvenssin, saadaan:

2, 2, 2, .. .

Koska kaikki sekvenssin ehdot toistetaan, on vahvistettu, että S on neliöllinen peräkkäin.

iii) peräkkäisyys s_Dif on säännöllinen ja sen syy r on 2. Käyttämällä aiemmin osoitettua yhtälöä R = 2 ∙ A, pysyy:

2 = 2 ∙ A, mikä tarkoittaa, että a = 1.

Erojen peräkkäin toinen termi S_Dif Se on 4 ja n-s_Dif On

A ∙ (2n+1)+b.

Toisella termillä on n = 2. Määritettiin myös, että a = 1, joten edellisen yhtälön käyttäminen ja sen korvaaminen on:

4 = 1 ∙ (2 ∙ 2+1)+B

Selvä B saadaan: b = -1.

On tiedossa, että S: n toinen termi on 2 arvoinen ja että yleisen termin kaavan on täytettävä n = 2: n:

T_n = A ∙ n² + B ∙ n +c; n = 2; A = 1; B = -1; T₂ = 2

Tarkoittaen

2 = 1 ∙ 2² - 1 ∙ 2 + C

Johtopäätöksenä on, että c = 0, toisin sanoen, että kaava, joka antaa peräkkäisyyden yleisen termin, on:

T_n = 1 ∙ N² - 1 ∙ n +0 = n² - n

Nyt viides termi on vahvistettu:

T₅ = 5² - 5 = 20

iii) Kuva #10, jota ei ole piirretty tähän, on alue, joka vastaa S -peräkkäin kymmenesosa:

T₁₀ = 10² - 10 = 90

Viitteet

1. https: // www.Geogebra.org