Vektorien graafisen menetelmän summa, esimerkit, ratkaisut harjoitukset

Se vektorien summa Toiseen vektoriin johtaa vektorien välinen lisäysoperaatio. Vektoreille on ominaista suuruusluokka ja myös suunta ja merkitys. Siksi niitä ei yleensä ole mahdollista lisätä, kuten se tehdään skalaarisiksi, ts. Numeroiden lisääminen.

Useiden vektorien summaa saatua vektoria kutsutaan tuloksena oleva vektori. Mekaniikassa puhumme tuloksena oleva voima, joka on kaikkien kehon voimien vektorisumma. Tämä tulos vastaa joukkoja.

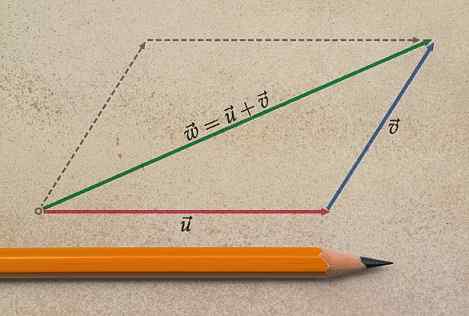
Summavektorin kokonaan määrittämiseksi on tarpeen ilmaista suuruus ja yhtenäisyys, suunta ja merkitys.

On tärkeää korostaa, että lisäämällä vektoreita niiden on oltava samaa fyysistä suuruutta, joten vektorisumma on homogeeninen operaatio. Tämä tarkoittaa, että voimme lisätä yhden voiman toisen kanssa, mutta ei siirtymän voimaa, koska tulos on merkityksetön.

Tuloksena olevan vektorin löytämiseksi on saatavana useita menetelmiä: grafiikka ja analytiikka. Vektorisummien löytämiseksi graafisilla menetelmillä se perustuu vektorin yksinkertaiseen esitykseen, nimittäin segmentisuuntautuneeseen tai nuoleen näin:

Vektorin graafinen esitys tasossa. Lähde: f. Zapata.

Vektorit merkitään mustilla kirjaimilla painetussa tekstissä tai nuolella kirjeessä, jotta ne voidaan erottaa niiden suuruuksista tai skalaarisista määristä. Esimerkiksi vektorin suuruus v Se on yksinkertaisesti v.

[TOC]

Graafinen menetelmä vektorien lisäämiseksi

Lisää enemmän kuin kaksi parisvektoria, Monikulmiomenetelmä jompikumpi monikulmio, joka koostuu siirtämisestä jokaiselle osoitetulle vektorille. Vektorien ominaisuus on, että ne ovat muuttumassa käännöksen suhteen, joten käytämme tätä ominaisuutta summan määrittämiseen.

Voi palvella sinua: Lämpölaajennus

Se alkaa millä tahansa vektorilla, koska vektorilisäys on kommutatiivinen ja lisäysjärjestys ei muuta summaa. Toinen vektori liikkuu alla, sovittaen sen alkuperän ensimmäisen loppuun.

Sitten se saatetaan seuraavaan vektoriin ja laitetaan sitten sama menettely, joka vastaa alkuperää edellisen loppuun. Jatkamme tällä tavalla viimeisen vektorin sijoittamiseksi.

Tuloksena oleva vektori on yksi, joka liittyy ensimmäisen alkuperään viimeisen vapaan pään kanssa. Tämän menetelmän nimi tulee tuloksesta: monikulmio.

Esimerkki

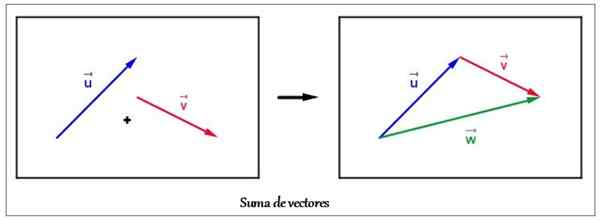
Summa esimerkki kahdesta tason vektorista graafisella menetelmällä. Lähde: Wikimedia Commons

Otetaan esimerkiksi kahden vektorin summa tai ja v Se on esitetty ylemmässä kuvassa.

Alkaen vektorista tai, Hän muutti vektoriin v Vastaamaan sen alkuperää ensimmäisen loppuun. Tuloksena oleva vektori W - Se on vedetty alkuperäisestä tai lopuksi v, Kolmipuolisen kuvan muodostaminen: kolmio. Siksi tässä erityistapauksessa menettelyä kutsutaan Kolmiomenetelmä.

Huomaa tärkeä yksityiskohta, tuloksena olevan vektorin suuruus tai moduuli ei ole lisävektorien moduulien summa. Itse asiassa se on melkein aina vähemmän, elleivät vektorit ole yhdensuuntaisia.

Katsotaanpa mitä tapahtuu tässä tapauksessa.

Erityinen tapaus: Rinnakkaisvektorien summa

Kuvattu menetelmä voidaan soveltaa myös erityistapaukseen, jossa vektorit ovat yhdensuuntaisia. Mieti seuraavaa esimerkkiä:

Voi palvella sinua: Boltzmann vakio: historia, yhtälöt, laskelmat, harjoituksetRinnakkaisvektorien summa. Lähde: f. Zapata.

Vektori on jäljellä v Alkuperäisessä asennossaan ja siirtyy vektoriin tai siten, että sen alkuperä on yhtä mieltä  v. Nyt vektori on peräisin v Ja loppu tai.

Tämä on tuloksena oleva vektori W - ja sen koko on mainosten koon summa. Kolmen vektorin suunta ja suunta on sama.

Tuloksena olevalla vektorilla on maksimimoduuli, jos lisäys muodostaa 0º kulman, kuten esimerkin. Jos vektorit muodostavat 180º kulman toistensa kanssa, tuloksena olevalla vektorilla on minimimoduuli.

Esimerkkejä vektorien summasta

- Siirtymät

Pyöräilijä matkustaa ensin 3 km: n suuntaan pohjoiseen ja sitten 4 km länteen. Siirtymäsi, jota kutsumme R -, Se löytyy helposti kolmiomenetelmästä plus referenssijärjestelmä, jossa kardinaalipisteet on merkitty:

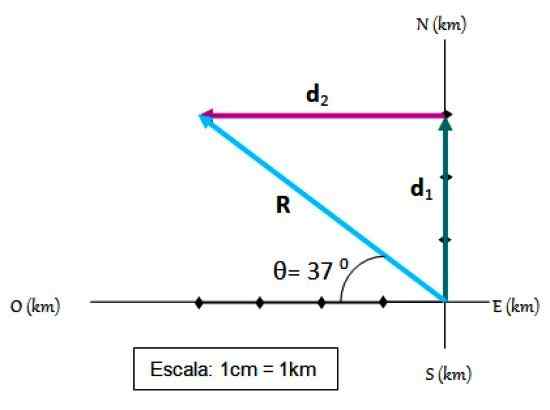Kahden siirron seurauksena. Lähde: f. Zapata.

Vaiheet lisätä vektori

-Lähtökohta osuu vertailujärjestelmän alkuperän kanssa.

-Koordinaattiakseleilla valitaan asteikko, joka tässä tapauksessa on 1 cm = 1 km

-Ensimmäinen siirtymä on piirretty mittakaavassa d -d_1.

-Sitten eräs d -d₁ Toinen siirtymä on piirretty d -d₂, Myös mittakaavassa.

-Tuloksena oleva siirtymä R - Se on vektori, joka menee alkuperästä loppuun d -d₂.

-Koko R - Se mitataan asteittaisella säännöllä, on helppo varmistaa, että r = 5.

-Lopuksi kulma että R - Muoto vaakasuunnassa mitataan kuljettajan avulla ja osoittautuu θ = 37 ^{0 -}

- Tuloksena oleva nopeus

Uimari haluaa ylittää joen ja tälle ei mitään nopeudella 6 km/h, kohtisuorassa rantaan, mutta virta, jonka nopeus on 4 km/h, poikkeaa.

Se voi palvella sinua: Ohm: Resistenssimittaukset, esimerkit ja liikunta ratkaistu

Tietämään sen tuloksena oleva nopeus, uimarinopeusvektorit lisätään, joka on piirretty pystysuoraan ja virran, joka on vaakasuora.

Graafisen menetelmän mukaisesti saadaan nopeus saadaan v_{R -}-

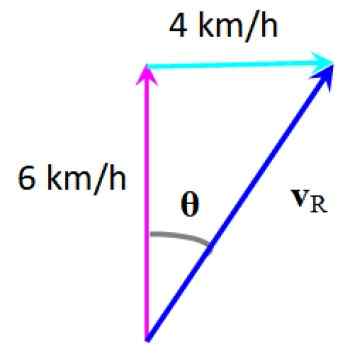Tuloksena oleva nopeus. Lähde: f. Zapata.

Uimurin kokenut poikkeama voidaan laskea:

θ = arctg (4/6) = 33.Alkuperäisen osoitteesi seitsemäs oikealla puolella

Sen nopeuden suuruutta lisääntyy, koska joen nopeus lisää vektorisesti. Löydät asteikon huolellisesti, kuten edellisessä esimerkissä.

Tai 33: n trigonometristen syiden avulla.Seitsemäs:

SEN 33.7. = 4/V_{R -}

v_{R -} = 4/ sin 33.7. = 7.21 km/h

Liikuntaa

Hiukkasessa seuraavat voimat, joiden suuruus on lueteltu alla:

F₁= 2.5 n; F₂= 3 n; F₃= 4 n; F₄= 2.5 n

Löydä tuloksena oleva voima.

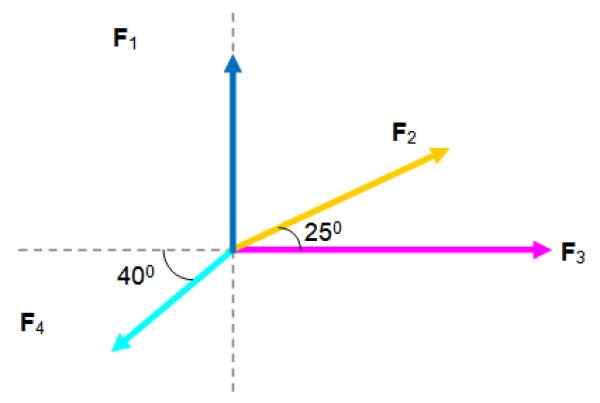Coplanar Force -järjestelmä. Lähde: f. Zapata.

Ratkaisu

Voimme lisätä graafisesti aloittamista mistä tahansa vektorista, koska vektorisumma on kommutatiivinen.

Kuvassa A alkoi F₁. Asteikon perustaminen ja säännön ja ryhmän avulla muut vektorit siirretään niiden sijoittamiseen peräkkäin.

Vektori F_{R -} on suunnattu F₁ lopuksi F₄. Sen suuruus on 5.2 n ja muodostaa 26 kulman.5. horisontaalista suhteessa.

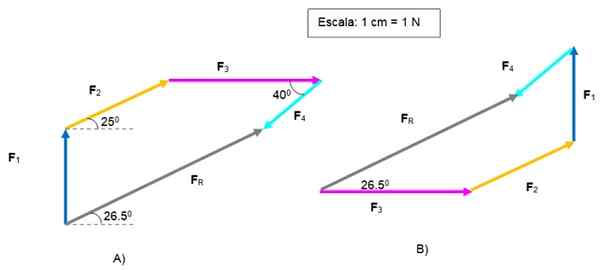Vektorigrafinen summa. Lähde: f. Zapata.

Kuvassa B sama ongelma ratkaistiin, alkaen F₃ ja päättyy F₄, Saada sama F_{R -} .

Polygonit ovat erilaisia, mutta tulos on sama. Lukija voi testata vektorien järjestyksen uudelleen.

Viitteet

1. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill.
2. Bedford, 2000. -Lla. Tekniikan mekaniikka: staattinen. Addison Wesley.
3. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Osa 1. Kinematiikka. Toimittanut Douglas Figueroa (USB).
4. Giambattista, a. 2010. Fysiikka. Toinen. Ed. McGraw Hill.
5. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Osa 1.