Rinnakkaisogrammimenetelmäesimerkit, ratkaistut harjoitukset

Hän rinnakkaisohjelma Se on graafinen menetelmä, jolla lisätään kaksi vektoria tasoon. Sitä käytetään usein löytämään tulokset kahdesta voimasta, jota käytetään runkoon tai kahteen nopeuteen, kuten uimarin tapauksessa, joka aikoo ylittää joen kohtisuorasti ja sen ohjataan virran ohjaamana.

Rinnakkaisogrammin rakentamiseksi lisättävien vektorien alkuperä, joka on piirretty mittakaavassa, on oltava samanaikaisesti pisteessä.

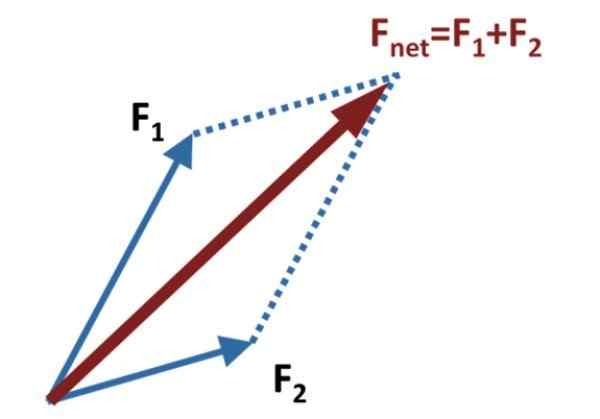
Kuvio 1. Rinnakkaisogrammimenetelmä kaksi vektoria. Lähde: Wikimedia Commons.

Sitten apuviivat piirretään jokaisen vektorin suuntaisesti, jotka saavuttavat toisen pään, kuten ylemmässä kuvassa esitetään.

Lisää tai tuloksena oleva vektori, jota kutsutaan myös nettovoimaksi, on vektori F_netto, Se saadaan piirtämällä vektori, joka menee F₁ ja F₂, siihen pisteeseen, että apulaitteet rinnakkaiset viivat leikkaavat. Kuvan kaaviossa nämä esitetään katkoviivoilla.

Menetelmä vastaanottaa nimensä kuviosta, joka on muodostettu addiktioilla ja apulinjoilla, mikä on tarkalleen rinnakkaisohjelma. Parallelogrammin tärkein diagonaali on summavektori.

On erittäin tärkeää korostaa, että ylimääräisten vektorien asettamisjärjestys ei muuta summaa, koska tämä vektorien välinen toiminta on kommutatiivinen.

[TOC]

Esimerkki rinnakkaisogrammimenetelmästä askel askeleelta

Seuraava kuva näyttää vektorit v ja tai Mielivaltaisissa yksiköissä. Vektori v Mitat 3.61 yksikköä ja muodostaa kulman 56.Kolmas vaakasuunnassa, kun taas tai Mitat 6.32 yksikköä ja kulma 18.4º tästä vertailulinjasta.

Voi palvella sinua: Satunnainen virhe: kaava ja yhtälöt, laskenta, esimerkit, harjoitukset

Löydämme vektorisi lisää rinnakkaisogrammimenetelmän kautta.

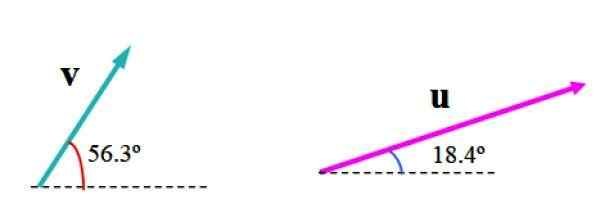Kuva 2. Kaikki kaksi tason vektoria, joista haluamme löytää tuloksena olevan vektorin. Lähde: f. Zapata

On tarpeen valita sopiva asteikko, kuten seuraavassa kuvassa esitetty, jossa taso on jaettu ruudulla. Neliön leveys edustaa yhtä (1) yksikköä.

Koska vektorit eivät muutu siirrettäessä, ne asetetaan siten, että heidän alkuperänsä vastaa koordinaattijärjestelmän alkuperää (vasemman kuva).

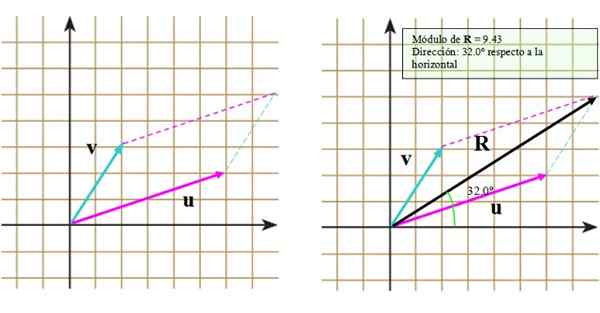Kuva 3. Vektorien summa rinnakkaisogrammimenetelmän avulla. Lähde: f. Zapata.

Noudataan nyt näitä vaiheita:

1. Vektori vektorin loppu v Segmentoitu viiva, joka on yhdensuuntainen vektorin kanssa tai.
2. Toista toimenpide, mutta tällä kertaa vektorin lopussa tai.
3. Piirrä tärkein diagonaali, joka ulottuu yleisestä alkuperästä segmentoitujen viivojen leikkauspisteeseen.

Tulos voidaan nähdä oikeassa kuvassa, jossa tuloksena oleva vektori ilmestyy R -.

Jos haluamme tietää suuruuden R -, Voimme mitata sen pituuden ja verrata sitä asteikkoon. Ja niiden suunnan suhteen vaaka -akselia tai pystysuuntaista akselia voidaan käyttää viitteinä, esimerkiksi.

Käyttämällä vaaka -akselia tai x -akselia, kulma, joka R - Muoto tällä akselilla mitataan kuljettimella ja tällä tavalla tiedämme osoitteen R -.

Myös R - Ne voidaan laskea kosinin ja rinnan lauseilla, koska muodostettu rinnakkaisohjelma voidaan jakaa kahteen yhtenäiseen kolmioon, joiden sivut ovat vektorien moduulit tai, v ja R -. Katso esimerkki ratkaistu 1.

Voi palvella sinua: hetkellinen nopeus: Määritelmä, kaava, laskenta ja harjoitukset

Erityinen tapaus: kohtisuoravektorien summa

Kun vektorit ovat kohtisuorassa toisiinsa nähden, muodostettu kuva on suorakulmio. Tuloksena oleva vektorimoduuli vastaa diagonaalin pituutta, joka voidaan helposti laskea Pythagoras -lauseen avulla.

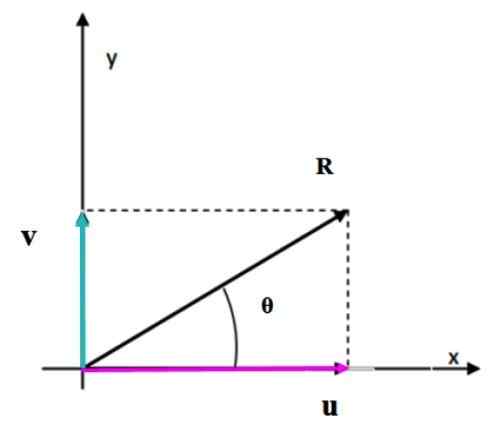Kuva 4. Kahden kohtisuoran vektorin summa käyttämällä rinnakkaisogrammimenetelmää. Lähde: f. Zapata.

Ratkaisut

- Harjoitus 1

Sinulla on vektori v, joka mittaa 3.61 yksikköä ja muodostaa kulman 56.Kolmas vaaka- ja vektori tai, jonka toimenpide on 6.32 yksikköä ja muodostaa 18 kulman.4. (kuva 2). Määritä tuloksena oleva vektorimoduuli R - = tai + v ja suunta, joka muodostaa mainittua vektoria vaaka -akselilla.

Ratkaisu

Rinnakkaisogrammimenetelmää käytetään edellä kuvattujen vaiheiden mukaan vektorin saamiseksi R -. Kuten aiemmin todettiin, jos vektorit piirretään huolellisesti asteikon jälkeen ja käyttämällä sääntöä ja kuljettajaa, suuruus ja suunta R - Ne mitataan suoraan piirustuksessa.

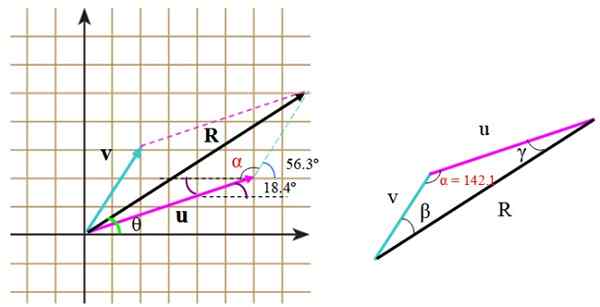Kuva 5.- Tuloksena olevan vektorin suuruuden ja suunnan laskeminen. Lähde: f. Zapata.

Ne voidaan myös laskea suoraan trigonometrian ja kulmien ominaisuuksien avulla. Kun muodostettu kolmio ei ole suorakulmio, kuten tässä tapauksessa, kosinuslause levitetään puuttuvan puolen löytämiseen.

Oikeassa kolmiossa sivut mittaavat u, v ja r. Kosinin lauseen soveltamiseksi on tarpeen tietää kulma v ja tai, että voimme löytää ruudukon avulla, asettamalla oikein lausunnon toimittamat kulmat.

Tämä kulma on α ja koostuu:

α = (90-56.3.) + 90º +18.4. = 142.Ensimmäinen

Voi palvella sinua: Punainen kääpiö

Coseno -lauseen mukaan:

R -² = v² + tai² - 2U⋅V⋅cos α = 3.61² + 6.32² - 23.61 × 6.32 × cos 142.1. = 88.98

R = 9.43 yksikköä.

Lopuksi kulma R - Ja vaaka -akseli on θ = 18.4 º + γ. Kulma γ löytyy rintalauseesta:

sin α / r = sen γ / u

Siksi:

sin γ = v (sin α / r) = 3.61 x (Sen 142.1. / 9.43)

γ = 13.Kuudes

θ = 18.4 º + 13.6 º = 32º

- Harjoitus 2

Uimari valmistautuu ylittämään joen uinnin kohtisuorassa virtaan nähden vakiona 2.0 m/s. Uimari alkaa A: sta, mutta se päättyy B, alavirran pisteeseen, johtuen sen ohjaamasta virrasta.

Jos virran nopeus on 0.8 m/s ja kaikkien nopeuksien on tarkoitus löytää uimarin nopeus, kuten tarkkailija seisoo rannalla.

Ratkaisu

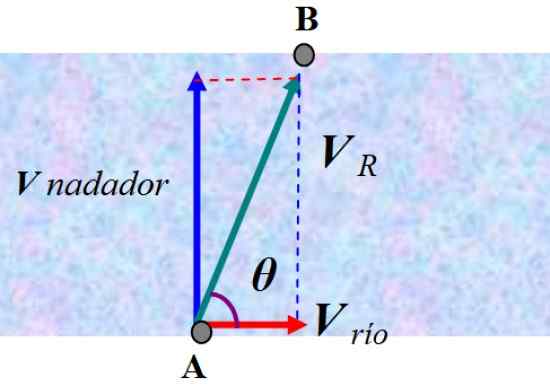Kuva 6. Nopeuden summa rinnakkaisogrammimenetelmällä. Lähde: f. Zapata.

Rannalla seisova tarkkailija näkisi kuinka uimari ohjataan tuloksena olevan nopeuden mukaan V_{R -}. Vastauksen löytämiseksi meidän on lisättävä uimareiden nopeus ja virran nopeus, jota kutsumme V _joki-

V _{R -} = V _uimari + V _joki

Kuvassa, jota ei ole mittakaavassa, vektorit lisättiin saamaan V _{R -.} Tässä tapauksessa Pythagoras -lause voidaan käyttää sen suuruuden saamiseksi:

V_{R -}² = 2.0 -² + 0 -.8² = 4.64

V_{R -} = 2.15 m/s

Osoite, jossa kohtisuoran suunnan uimari lasketaan helposti, huomaa sen:

θ = arctg (2/0.8) = 68.Toinen

Sitten uimari poikkeaa 90º - 68.2nd = 27.2. alkuperäisestä osoitteestasi.

Viitteet

1. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill.
2. Bedford, 2000. -Lla. Tekniikan mekaniikka: staattinen. Addison Wesley.
3. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Osa 1. Kinematiikka. Toimittanut Douglas Figueroa (USB).
4. Giambattista, a. 2010. Fysiikka. Toinen. Ed. McGraw Hill.
5. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Osa 1.