Bernoulli -lause

Selitämme, mikä on Bernoullin lause, yhtälöt, sovellukset ja ratkaisemme harjoituksen

Mikä on Bernoullin lause?

Hän Bernoulli -lause Hän vakuuttaa, että putken mekaaninen energia kohden ihanteellisessa nesteessä, joka kiertää putken osioissa, mekaaninen energiaa kohden, riippumatta siitä, että niillä on erilainen poikittainen alue pinta -alasta ja korkeudesta.

Nyt ihanteellinen neste on se, jota ei voida puristaa, joten sen tiheys on kiinteä, painearvosta riippumatta.

Lisäksi ihanteellisella nesteellä on nolla viskositeetti, ts. Nestekerrosten välillä ei ole kitkaa eikä nesteen ja kanavan seinämien välillä.

Puristamattomuuden ja nolla -viskositeetin olosuhteet ovat välttämättömiä Bernoullin lauseen soveltamiseksi. On myös välttämätöntä, että virtaus on paikallaan, ts. Virtaus ei vaihtele ajan myötä.

Toisaalta virtauksen on oltava laminaarista, joten kanavan kulkujen aikana ei voi olla pyörteitä tai turbulenssia.

Bernoulli -yhtälö

Bernoulli -yhtälöllä on kolme termiä, paineen P, kineettinen energia ja gravitaatiopotentiaalienergia jokaiselle tilavuustiheydelle nesteyksikölle ρ

Bernoullin yhtälö on:

Toisaalta jatkuvuusyhtälö vahvistaa, että ihanteellisessa nesteessä virtaus on vakio virtausputken kaikissa osissa. Toisin sanoen nesteen tilavuus samassa ajan yksikössä on sama putken kaikissa osissa.

Jos virtaus on q, niin:

Q = vakio

Kanssa:

Q = a · v

Missä a on putken poikkileikkausalue ja v on nesteen nopeus.

Voi palvella sinua: keinotekoiset satelliitit

On huomattava, että putken kapeimmissa osissa nesteen on kiertävä nopeammin, koska se pysyy vakiona, vaikka se vaihtelee. Siksi kineettinen energia tilavuusyksikköä kohti on suurempi.

Koska Bernoullin lause osoittaa, että mekaaninen energia on vakio kaikissa osissa, suuremman kineettisen energian kapeammissa osissa potentiaalienergia vähenee. 

Potentiaalinen energia koostuu painovoimaa kohti tilavuutta kohti plus paineen tekemä työ yksikkötilavuudella, siten vähentämällä potentiaalienergiaa myös vähentää painetta.

Yhteenvetona voidaan todeta, että jatkuvuusperiaatteen ja Bernoullin lauseen yhdistelmävaikutus johtaa virtausputken kapeisiin osiin, joissa nesteenopeus on suurempi, paine laskee laajempien osien suhteen.

Bernoulli -yhtälön termit

1) Paineessa oleva työ tilavuusyksikköä kohti 

Alueen poikkileikkausosassa, Neste siirtää määrän s, Paine P: n takia, joka tuottaa voiman f = p⋅ a.

Voimalla tehty työ on:

F⋅ s = p⋅ a⋅ s

Koska A⋅s -tuote edustaa siirrettyjä tilavuutta, silloin tehtävät työmäärää kohti tehdyt työt vastaavat numeerisesti P: n arvoa tarkasteltavassa osassa.

2) Nesteen yksikkömäärän kineettinen energia

Koska neste on puristamaton, sen tiheydellä on kiinteä arvo nimeltään ρ.

Kun neste kiertää poikkileikkauksen A osan läpi, siirtämällä määrää S aikana t, virtausnopeus on:

Se voi palvella sinua: termodynamiikan toinen laki: kaavat, yhtälöt, esimerkit

v = s/t

Ja mainitun nesteen osan kineettinen energia lasketaan:

K = ½ ρ (a⋅s) V²

Mutta jos siirtynyt tilavuus (A⋅s) on yksikkö, niin kineettisen energian termi annetaan ½ ρ V: llä².

3) Yksikkön määrän nesteen määrän painovoima potentiaalien energia korkeudella H 

Taikinan nesteosaan m ja korkeus h Tietyn vertailutason suhteen gravitaatioenergia annetaan:

U = m⋅ g⋅ h

Jos taikina m Se vastaa yhtenäistä nesteosaa, sitten osan massa vastaa tiheyttä ρ, Joten potentiaalinen energia on ρ⋅ g⋅ h.

Bernoulli -lauseiden sovellukset

Aerodynaaminen tuki

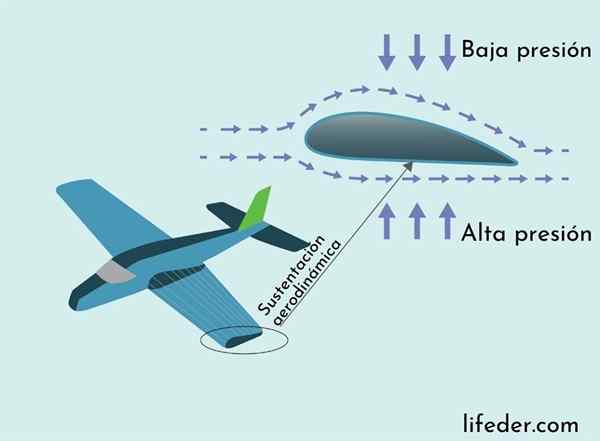Aerodynaaminen tuki selitetään Bernoullin lauseella

Voima, joka estää lentokoneen lennon romahtamisen, on aerodynaaminen tukivoima. Verkkotukivoima on suunnattu pystysuoraan ja toimii koneen siipiä pitkin. Sen alkuperä selitetään Bernoullin lauseen kautta.

Tason siipissä on poikkileikkaus, jonka yläosassa on pidempi käyrä ja alaosassa lyhyempi. Tämä tekee lentoreitin lähellä siipin pintaa yläosassa, joten ilma virtaa nopeammin siipien yläpuolelle kuin pohja. 

Bernoullin lauseen seurauksena kiertävän siipin yläosassa oleva ilmanpaine on pienempi kuin alareunassa, mikä johtaa paine -eroon kohdistuvaan voimaan, joka tukee tason painoa, sen mukaan voi olla Seuraavassa kuvassa.

Se voi palvella sinua: fysiikka kreikkalaisten aikana (Antige Kreikka)

KÄYTTÖÖN PALJON LÄHETÄ

Joissakin urheilulajeissa, kuten jalkapallo, baseball ja Cricke, kokenut pelaajat tietävät miten. On niin kutsuttu Efektin käynnistys.

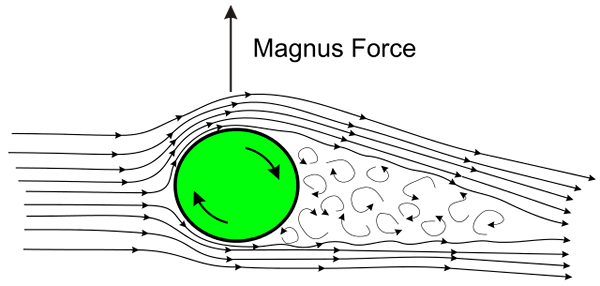Magnus Effect -kuva. Lähde: Wikimedia Commons

Vaikutus tapahtuu aina, kun pallo tai pallo kääntyy nopeasti liikkuessaan ilman läpi. Kierto aiheuttaa ilman pallon pinnalle, se vetää sen kahteen vastakkaiseen suuntaan, toinen käännössuuntaan ja toisella puolella, siirtymissuunnan vasten.

Ilmavedon seurauksena matalapaineinen alue tuotetaan pallon pinta -alalle ja vastakkaisella kasvolla korkea paine, mikä tuottaa verkkovoiman, joka ohjaa pallon luonnollisen etenemissuunnan.

Tämän ilmiön selitys, joka tunnetaan nimellä Magnus -vaikutus Se sijaitsee tarkasti Bernoullin lauseessa: missä neste kiertää nopeasti, paine on alhainen ja sivulla, jossa paine kiertää hitaasti.

Liikuntaa

Vaakaputkessa on alue -osa A₁ = 40 neliö senttimetriä ja toinen osa alueen osasta A₂ neljä kertaa alhaisempi. Jos veden virtaus on 6 l/s, määritä paine -ero ja korkeusero pystysuorissa putkissa.

Ratkaisu 

Alkaen virtausyhtälöstä, jonka arvo on q = 6 l/s:

Q = a · v

Sinun on silloin leveän osan nopeus 1,5 m/s ja kapeassa venytyksessä 6 m/s.

Sitten saadaan Bernoulli -yhtälön leveä ja kapean venytyksen leveä ja kapea, paine -ero on 1700 PA: ta, mikä vastaa korkeuseroa pystysuorissa putkissa 1,72 metriä.