Euclid -lause

Mikä on Euclidin lause?

Hän Euclid -lause Se osoittaa oikean kolmion ominaisuudet piirtämällä viivan, joka jakaa sen kahteen uuteen suorakulmioon, jotka ovat samanlaisia ​​toistensa kanssa ja puolestaan ​​ovat samanlaisia ​​kuin alkuperäinen kolmio; Joten on suhteellisuussuhde.

Euclides oli yksi suurimmista vanhuuden matemaatikoista ja geometreistä, jotka tekivät useita mielenosoituksia tärkeistä lauseista. Yksi tärkeimmistä on se, joka kantaa hänen nimensä, jolla on ollut laaja sovellus.

Tämä on ollut niin siksi, että sen lauseen kautta suorakulmiokolmiossa olevat geometriset suhteet selittävät, missä tämä liittyy heidän ennusteisiinsa hypotenusessa.

Kaavat ja esittely

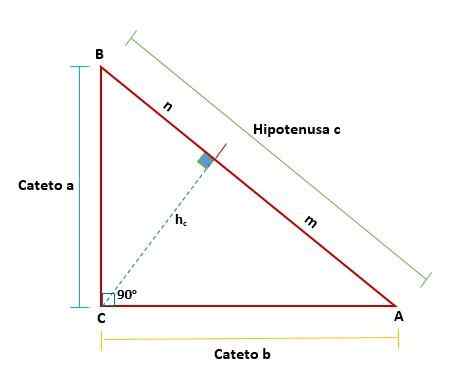
Euclid -lause ehdottaa, että jokaisessa oikeassa kolmiossa, kun rivi piirretään - joka edustaa oikean kulman kärkeä vastaavaa korkeutta hypoteenin suhteen - alkuperäisistä kolmioista muodostuu kaksi suorakulmiota alkuperäisestä kolmiosta alkuperäisestä.

Nämä kolmiot ovat samanlaisia ​​toistensa kanssa ja ovat myös samanlaisia ​​kuin alkuperäinen kolmio, mikä tarkoittaa, että niiden samanlaiset sivut ovat verrannollisia toisiinsa:

Kolmen kolmion kulmat ovat yhdenmukaisia; Eli kun se pyöritetään 180 asteessa sen kärkillä, kulma tapahtuu toisella. Tämä tarkoittaa, että kaikki ovat tasa -arvoisia.

Tällä tavalla voit myös tarkistaa kolmen kolmion välillä olemassa olevan samankaltaisuuden, sen kulmien tasa -arvon suhteen. Kolmioiden samankaltaisuuden jälkeen Euclid määrittelee niiden osuudet kahdesta lauseesta:

• Korkeuslause.
• Catetos -lause.

Tällä lauseella on laaja sovellus. Muinaisina aikoina sitä käytettiin korkeuksien tai etäisyyksien laskemiseen, mikä edustaa suurta edistystä trigonometrialle.

Voi palvella sinua: lähestymistapojen laskeminen erottelujen avulla

Sitä sovelletaan tällä hetkellä matematiikkaan perustuvilla alueilla, kuten tekniikka, fysiikka, kemia ja tähtitiede, monien muiden alueiden joukossa.

Korkeuslause

Tämä lause toteaa, että missä tahansa suorakulmiokolmiossa oikean kulmasta vedetty korkeus hypotenusiin nähden on geometrinen suhteellinen keskiarvo (korkeuden neliö) kotetojen projektioiden välillä, jotka määrittelevät hypotenuseuseissa.

Toisin sanoen korkeuden neliö on yhtä suuri kuin hypotenusen muodostavien jalkojen kertominen:

h_c² = m _* n

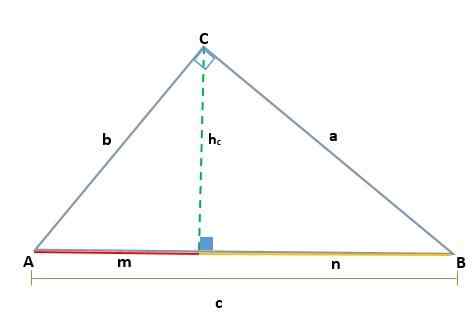
Esittely

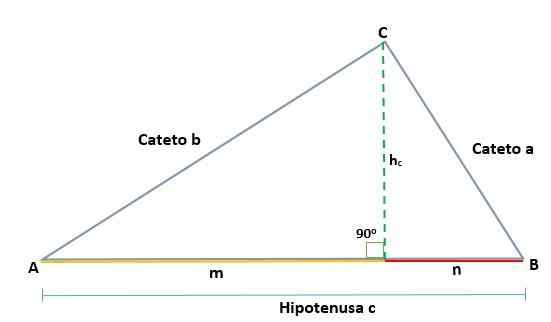
Kun otetaan huomioon ABC -kolmio, joka on suorakulmio kärjessä C, syntyy kaksi samanlaista suorakulmiota, ADC ja BCD; Siksi niiden vastaavat puolet ovat verrannollisia:

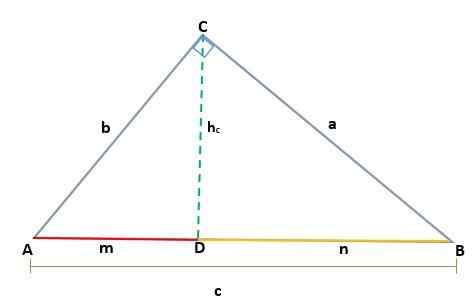
Siten, että korkeus h_c Se vastaa CD -segmenttiä, vastaa hypotenusia AB = C, joten sinun on:

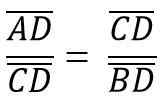
Tämä puolestaan ​​vastaa:

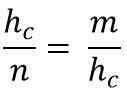
Hypotenusen puhdistaminen (H_c), Kertoaksesi kaksi tasa -arvon jäsentä, sinun on:

h_{C *} h_{C =} m _* n

h_c² = m _* n

Siten hypotenusen arvo annetaan:

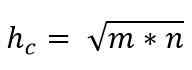
Catetos -lause

Tämä lause toteaa, että jokaisessa oikeassa kolmiossa kunkin kateton mitta on geometrinen suhteellinen keskiarvo (kunkin cateton neliö) hypoteenin mittauksen (täydellinen) ja sen jokaisen projisoinnin välillä:

b -² = c _* m

-lla² = c_* n

Esittely

Kun otetaan huomioon ABC -kolmio, joka on suorakulmio kärjessä C, niin että sen hypotenusa on C, kun piirtävät korkeutta (h) luokkien A ja B projektiot määritetään, jotka ovat vastaavasti segmentit M ja N ja jotka ovat päällä, ja jotka ovat päällä Hypotenuse.

Siten suorakulmiokolmioon piirretty korkeus ABC tuottaa kaksi samanlaista suorakulmiota, ADC ja BCD, niin että vastaavat sivut ovat verrannollisia, kuten tämä:

Voi palvella sinua: Hyperbolinen paraboloidi: Määritelmä, ominaisuudet ja esimerkit

Db = n, joka on CB Cateton projektio hypotenusessa.

Ad = m, joka on AC Cateton projektio hypotenusessa.

Sitten hypotenuse C määritetään sen projektioiden jalkojen summan perusteella:

C = m + n

ADC- ja BCD -kolmioiden samankaltaisuuden vuoksi sinun on:

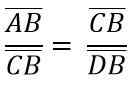
Yllä oleva on sama kuin:

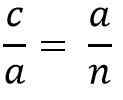
Selvää "A" Cateto moninkertaistaaksesi kaksi tasa -arvon jäsentä, sinun on:

-lla _* a = c _* n

-lla² = c _* n

Siten kateto “a” -arvo on antanut:

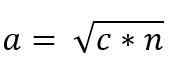
Samoin ACB- ja ADC -kolmioiden samankaltaisuuden vuoksi sinun on:

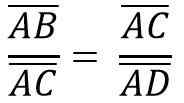
Yllä oleva on yhtä suuri kuin:

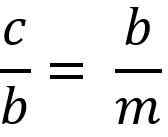
Selvitetään "B" Cateto moninkertaistaaksesi kaksi tasa -arvon jäsentä, sinun on:

b - _* b = c _* m

b -² = c _* m

Siten Catoto “B” -arvo on annettu:

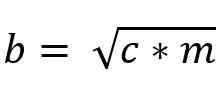
Euclid -lauseiden välinen suhde

Lauseet, jotka viitataan korkeuteen ja luokkiin, liittyvät toisiinsa, koska molempien mitta tehdään suorakulmion kolmion hypotenusiin.

Euclid -lauseiden suhteen löytyy myös korkeuden arvo; Se on mahdollista puhdistamalla luokan lauseen M ja N arvot ja korvataan korkeuslauseessa. Tällä tavalla on täytettävä, että korkeus on yhtä suuri kuin jalkojen kertominen, jaettuna hypotenusella:

b -² = c _* m

m = b² ÷ c

-lla² = c _* n

n = a² ÷ c

Korkeuslause M ja N korvataan:

h_c² = m _* n

h_c² = (b² ÷ c) _* (² ÷ c)

h_c = (b² _* -lla²) ÷ c

Ratkaisut

Esimerkki 1

Kun otetaan huomioon ABC -kolmio, suorakulmio A: ssa, määritä AC: n ja AD: n mitta, jos AB = 30 cm ja BD = 18 cm

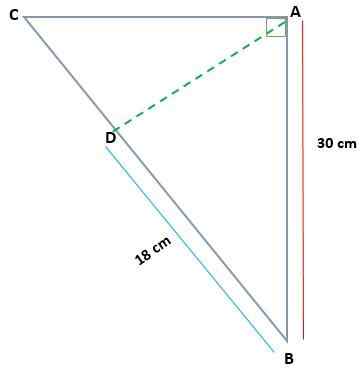
Ratkaisu

Tässä tapauksessa on olemassa yhden projisoidun jalan (BD) mitat ja yhden alkuperäisen kolmion tarar (AB). Tällä tavalla voit käyttää luokkalausetta löytääksesi BC Cateto -arvo.

Voi palvella sinua: toiminnon kirjeenvaihtosääntö

Ab² = BD _* BC

(30)² = 18 _* BC

900 = 18 _* BC

BC = 900 ÷ 18

BC = 50 cm

CD Cateton arvo löytyy tietäen, että BC = 50:

CD = BC - BD

CD = 50 - 18 = 32 cm

Nyt on mahdollista määrittää AC Cateton arvo, soveltamalla uudelleen luokkalausetta:

Ac² = CD _* Bd

Ac² = 32 _* viisikymmentä

Ac² = 160

AC = √1600 = 40 cm

Korkeuden arvon (AD) määrittämiseksi korkeuslause sovelletaan, koska projisoitujen kategorioiden arvot CD ja BD ovat tiedossa:

ILMOITUS² = 32 _* 18

ILMOITUS² = 576

AD = √576

AD = 24 cm

Esimerkki 2

Määritä MNL -kolmion korkeuden (H) arvo, suorakulmio n: ssä, segmenttien mittausten tunteminen:

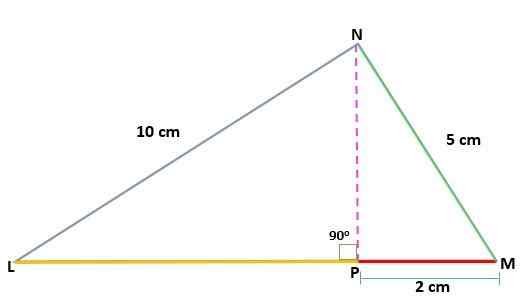
Nl = 10 cm

Mn = 5 cm

PM = 2 cm

Ratkaisu

Sinulla on mitattu yksi hypotenuseista (PM) projisoiduista jaloista, samoin kuin alkuperäisten kolmiokategorioiden mitat. Tällä tavoin voit käyttää luokkalausetta löytääksesi toisen projisoidun Catoton (LN) arvon:

Nl² = Pm _* Lm

(10)² = 5 _* Lm

100 = 5 _* Lm

PL = 100 ÷ 5 = 20

Koska luokkien arvo ja hypotenuse on jo tiedossa, korkeuslauseiden ja luokkien suhteen voidaan määrittää korkeuden arvo:

Nl = 10

Mn = 5

LM = 20

H = (b² _* -lla²) ÷ c.

H = (10² _* 5²-A  ÷ (kaksikymmentä)

H = (100 _* 25) ÷ (kaksikymmentä)

H = 2500 ÷ kaksikymmentä

H = 125 cm.