Norton -lauseen kuvaus, sovellukset, esimerkit ja harjoitukset

Hän Norton -lause, joka koskee sähköpiirejä, toteaa, että lineaarinen piiri, jolla on kaksi liitin A ja B, voidaan korvata toisella täysin vastaavalla, joka koostuu virran lähteestä, nimeltään I_Ei kytketty rinnakkain vastus r_Ei.

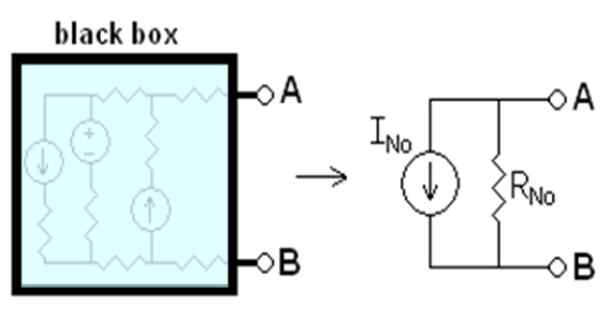
Sanoi nykyinen i_Ei kuulin_N Se virtaa pisteiden A ja B välillä, jos ne olisivat lyhyitä piirikirjoja. Vastus r_N Se on vastaava vastus terminaalien välillä, kun kaikki riippumattomat lähteet deaktivoidaan. Kaikki sanottu on suunniteltu kuvassa 1.

Kuvio 1. Nortonin vastaava piiri. Lähde: Wikimedia Commons. Drumkid [CC BY-SA 3.0 (http: // creativecommons.Org/lisenssit/by-SA/3.0/]]

Kuvan musta laatikko sisältää lineaarisen piirin, joka korvataan sen Norton -ekvivalentilla. Lineaarinen piiri on sellainen, jossa tulolla ja lähtöllä on lineaarinen riippuvuus, kuten jännitteen V ja tasavirran I välinen suhde ohmisessa elementissä: v = i.R -.

Tämä lauseke vastaa Ohmin lakia, jossa R on vastus, joka voi olla myös impedanssi, jos se on vaihtovirtapiiri.

Nortonin lauseen ovat kehittäneet sähköinen ja keksijä Edward L -insinööri. Norton (1898-1983), joka työskenteli pitkään Bell Laboratories.

[TOC]

Norton -lauseen sovellukset

Kun heillä on erittäin monimutkaisia ​​verkkoja, joilla on monia vastus- tai impedansseja ja haluat pienemmän ja hallittavan piirin.

Tällä tavoin Nortonin lause on erittäin tärkeä suunnitellessasi piiriä, joilla on useita elementtejä, ja heidän vasteensa tutkimiseksi.

Nortonin ja Theveninin lauseiden välinen suhde

Nortonin lause on kaksinkertainen Thevenin -lause, mikä tarkoittaa, että ne ovat vastaavia. Theveninin lause osoittaa, että kuvan 1 musta laatikko voidaan korvata sarjan jännitelähteellä, jolla on vastus, nimeltään Thevenin R -vastus_Th. Tämä ilmaistaan ​​seuraavassa kuvassa:

Voi palvella sinua: Materiaalimekaniikka: Historia, opiskelukenttä, sovellukset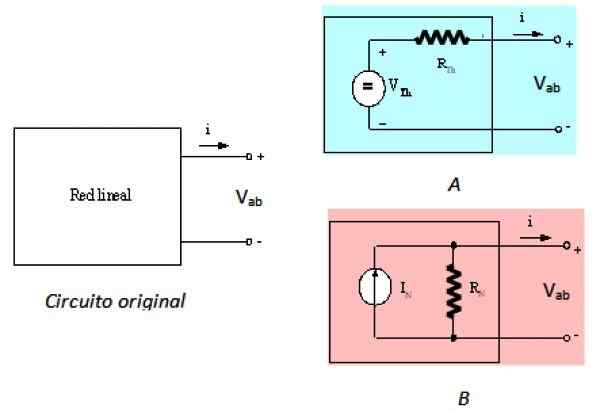 Kuva 2. Alkuperäinen vasen piiri ja sen vastaavat Théveniniltä ja Nortonilta. Lähde: f. Zapata.

Vasen piiri on alkuperäinen piiri, mustan laatikon lineaarinen verkko, oikeanpuoleinen piiri on ekvivalentti Thevenin ja Piiri ekvivalentti B - Se on Nortonin vastaava, kuten on kuvattu. Pitterminaaleista A ja B, kolme piiriä ovat vastaavia.

Huomaa nyt:

-Alkuperäisessä piirissä liitteiden välinen jännitys on V_Ab.

-V_Ab  = V_Th piirissä -Lla

-Lopuksi v_Ab  = I_N.R -_N piirissä B -

Jos liittimet A ja B ovat oikosulku kolmessa piirissä, on täytettävä, että jännitteen ja näiden pisteiden välisen virran on oltava samat kolmelle, koska ne ovat vastaavia. Niin:

-Alkuperäisessä piirissä virta on minä.

-Piirille A virta on I = V_Th / R_Th, Ohmin lain mukaan.

-Lopuksi piirissä B virta on minä_N

Siksi päätellään, että Nortonin ja Theveninin vastus on sama arvo ja että virra on antanut:

i = i_N = V_Th / R_Th = V_Th / R_N

Esimerkki

Nortonin lauseen oikein soveltamiseksi seuraavia vaiheita noudatetaan:

-Piiriosa, jota varten Norton -ekvivalentti löytyy verkosta, eristetään verkosta.

-Osoita jäljellä olevassa piirissä liittimet a ja b.

-Vaihda jännitelähteet oikosulkulla ja virrassa avoimilla piireillä löytääksesi vastaava vastus liittimien A ja B välillä. Tämä on r_N.

-Palauta kaikki lähteet alkuperäisiin asentoihinsa, lyhyet piirtävät päätteet A ja B ja löydä niiden välillä kiertävä virta. Tämä on minä_N.

Voi palvella sinua: Doppler -vaikutus: Kuvaus, kaavat, tapaukset, esimerkit

-Piirrä Norton -ekvivalentti piiri kuvassa 1 ilmoitettujen mukaan. Sekä virran lähde että vastaava vastus ovat rinnakkain.

Voit myös käyttää Theveninin lausetta löytääksesi r_Th, että tiedämme jo olevan yhtä suuri kuin r_N, Sitten Ohmin laki löydät minut_N Ja tuloksena oleva piiri on piirretty.

Ja nyt katsotaanpa esimerkki:

Löydä Nortonin vastaava seuraavan piirin pisteiden A ja B välillä:

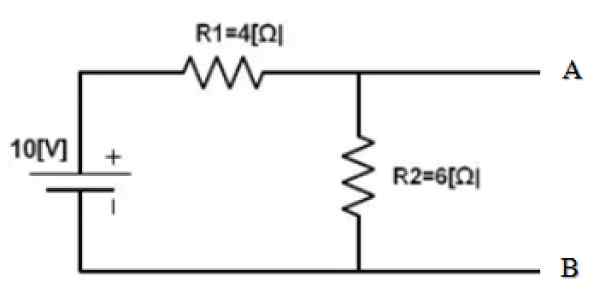Kuva 3. Esimerkkipiiri. Lähde: f. Zapata.

Piirin osa on jo eristetty, jonka vastaava on löydettävä. Ja kohdat A ja B määritetään selvästi. Seuraava on oikosulku 10 V lähde ja löydä saadun piirin vastaava vastus:

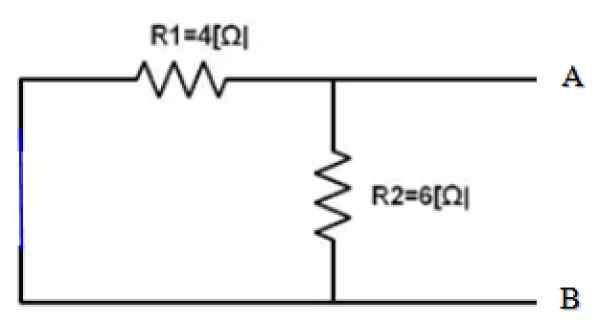Kuva 4. Lyhytpiirin lähde. Lähde: f. Zapata.

Näkymät terminaaleista A ja B, molemmat vastustusresenssit r₁ ja r₂ Siksi ne ovat rinnakkain:

1/r_Eq = 1/r₁₂ = (1/4) + (1/6) ω^-1 = 5/12 Ω^-1  → R_Eq = 12/5 ω = 2.4 Ω

Sitten lähde palautetaan paikkaansa ja pisteet A ja B ovat lyhyitä piirteitä löytääkseen sieltä kiertävän virran, tämä on_N. Siinä tapauksessa:

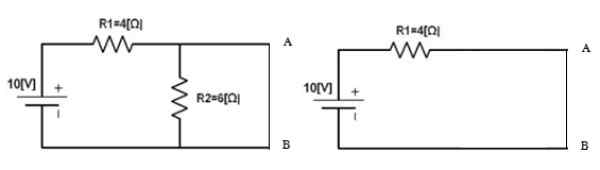Kuva 5. Piiri Norton -virran laskemiseksi. Lähde: f. Zapata.

Yllyttää_N = 10 V / 4 ω = 2.5 a

Nortonin vastaava

Lopuksi Nortonin vastaava arvojen kanssa on piirretty:

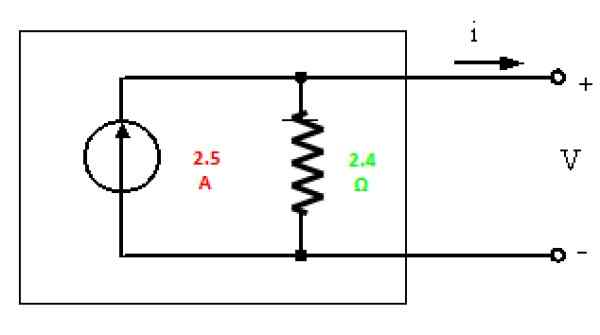Kuva 6. Piirin Norton -ekvivalentti kuvassa 3. Lähde: f. Zapata.

Liikuntaa

Seuraavan kuvan piirissä:

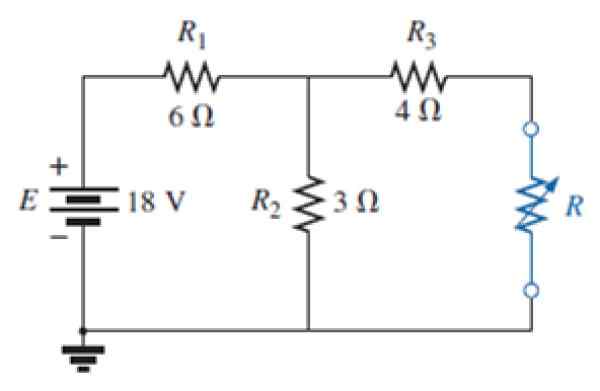Kuva 7. Piiri liikuntaa varten. Lähde: Alexander, c. 2006. Sähköpiirin säätiöt. Kolmas. Painos. MC Graw Hill.

a) Löydä Nortonin ulkoisen sinisen vastusverkon vastaava piiri.

b) Löydä myös Théveninin vastaava.

Liittää jhk

Edellä esitettyjen vaiheiden jälkeen lähteen on oltava lyhyt piiriki:

Voi palvella sinua: äänen diffraktio: mikä koostuu esimerkeistä, sovelluksista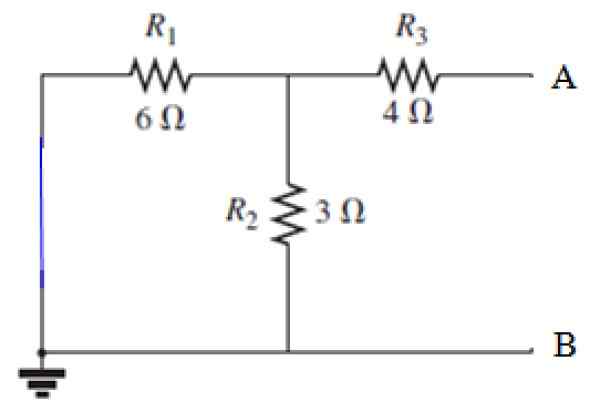 Kuva 8. Lyhyen piirin lähde piirissä kuvassa 7. Lähde: f. Zapata.

RN -laskenta

Näkymä terminaaleista a ja b, vastus r₃ on sarjassa rinnakkain muodostettu vastus r: stä₁ ja r₂, Lasketaan ensin tämän rinnakkaisen vastaava vastus:

1/r₁₂ = (1/6)+ (1/3) ω^-1 = 1/2 Ω^-1  → R_Eq = 2/1 ω = 2Ω

Ja sitten tämä rinnakkainen on sarjassa r kanssa_3, Joten vastaava vastus on:

R -_Eq = 2 ω + 4 ω = 6 Ω

Tämä on molempien r_N alkaen r_Th, Kuten aiemmin selitettiin.

Laskeminen

Sitten päätteet A ja B ovat lyhyitä piirikirjoja, palauttaen lähteen paikoilleen:

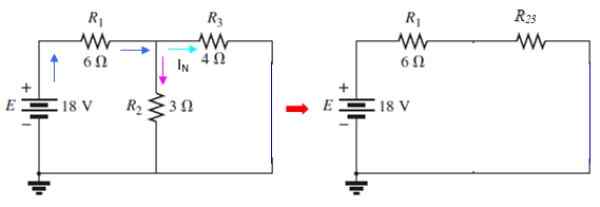Kuva 9. Norton -virran piirit. Lähde: f. Zapata.

Virta kulkee läpi i₃ on nykyinen I_N haet, joka voidaan määrittää mesh -menetelmällä tai käyttämällä sarjaa ja rinnakkaista. Tässä piirissä r₂ ja r₃ Ne ovat rinnakkain:

1/r₂₃ = (1/3)+ (1/4) ω^-1 = 7/12 Ω^-1  → R₂₃ = 12/7 Ω

Vastus r₁ Se on sarjassa tämän rinnakkain, sitten:

R -₁₂₃ = 6 + (12/7) ω = 54/7 Ω

Lähteestä (sininen väri) tulee nykyinen virta OHM: n laki:

V = i. R → i = v/r = 18 V/(54/7 ω) = 7/3 a

Tämä virta on jaettu kahteen osaan: toinen, joka ylittää r₂ Ja toinen, joka ylittää r₃. Kuitenkin virta, joka ylittää rinnakkaisen r₂₃ Se on sama, joka kulkee R: n läpi₁, kuten voidaan nähdä kuvan välipiirissä. Jännite on:

V₂₃ = I.R -₂₃ = (7/3) a .(12/7) ω = 4 V

Molemmat vastukset r₂ ja r₃ He ovat tällä jännitteellä, koska ne ovat rinnakkain, siksi:

Yllyttää₃ = V₂₃ / R₃ = 4 V / 4 ω = 1 a

Meillä on jo haku Norton -virta, koska kuten aiemmin sanoit, minä₃ = I_N, niin:

Yllyttää_N = 1 a

Nortonin vastaava

Kaikki on valmis piirtämään tämän piirin Norton -ekvivalentin pisteiden A ja B välillä:

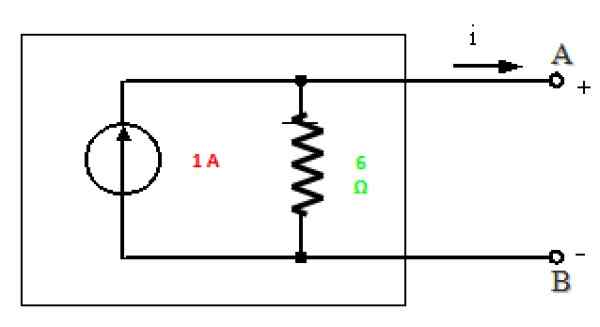Kuva 10. Piirin Norton -ekvivalentti kuvassa 7. Lähde: f. Zapata.

Ratkaisu b

Théveninin vastaavan löytäminen on hyvin yksinkertaista, koska r_Th = R_N= 6 Ω ja kuten edellisissä osissa selitetään:

V_Th = I_N. R -_N = 1 a . 6 ω = 6 V

Théveninin vastaava piiri on:

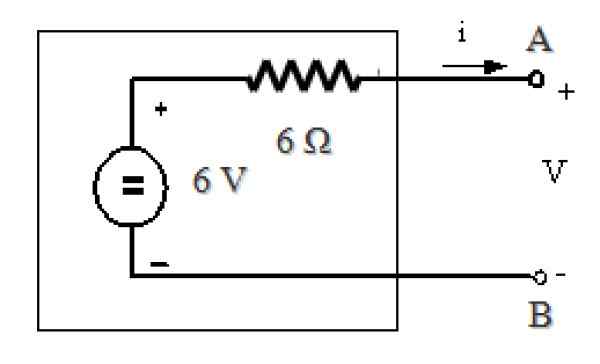Kuva 11. Theveninin vastine piiristä kuvassa 7. Lähde: f. Zapata.

Viitteet

1. Alexander, c. 2006. Sähköpiirin säätiöt. Kolmas. Painos. MC Graw Hill.
2. Boylestad, r. 2011. Johdanto piirianalyysiin. Toinen. Painos. Pearson.
3. Dorf, r. 2006. Johdatus sähköjoukkoihin. Seitsemäs. Painos. John Wiley & Sons.
4. Edminister, J. 1996. Sähköpiirit. Schaum -sarja. Kolmas. Painos. MC Graw Hill.
5. Wikipedia. Norton -lause . Palautettu: se on.Wikipedia.org.