Köysi (geometria) pituus, lause ja harjoitukset

Eräs köysi, Litteässä geometriassa linjasegmentti liittyy kahteen pisteeseen käyrästä. Sanotaan, että tätä segmenttiä sisältävä viiva on kuivausviiva käyrälle. Se on usein kehä, mutta voit varmasti piirtää jouset moniin muihin käyriin, kuten ellipsit ja vertaukset.

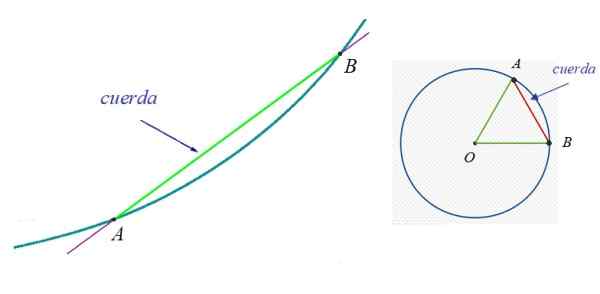
Kuviossa 1 vasemmalla on käyrä, johon pisteet A ja B kuuluvat. Köysi A: n ja B: n välillä on vihreä segmentti. Oikealla on kehä ja yksi heidän jousistaan, koska on mahdollista jäljittää ääretön.

Kuvio 1. Vasemmalla puolella mielivaltaisen käyrän köysi ja ympyrän köysi oikealle. Lähde: Wikimedia Commons.

Ympäristössä sen halkaisija on erityisen mielenkiintoinen, mikä tunnetaan myös nimellä Pääke. Se on köysi, joka sisältää aina kehän keskustan ja mittaa kahdesti sädettä.

Seuraavaa kuvaa edustaa säde, halkaisija, köysi ja myös ympyrän kaari. Jokaisen tunnistaminen on tärkeää, kun ratkaiset ongelmia.

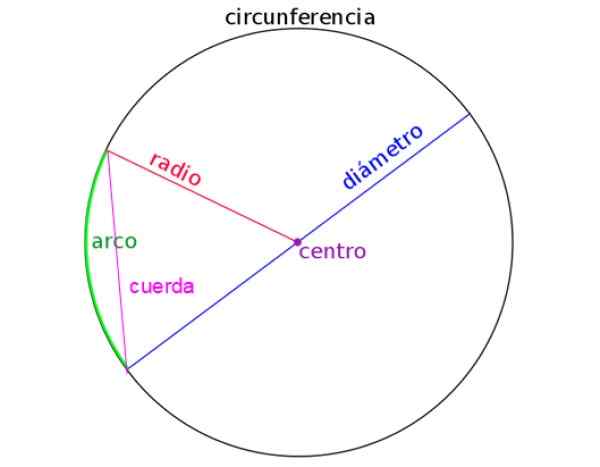Kuva 2. Kehän elementit. Lähde: Wikimedia Commons.

[TOC]

Kehän köyden pituus

Voimme laskea köyden pituuden ympyrässä, joka alkaa kuvioista 3a ja 3b. Huomaa, että kolmio on aina muodostettu kahdella yhtä suurella puolella (tasapeli): OA- ja OB -segmentit, jotka mittaavat r, kehän säde. Kolmion kolmas puoli on segmentti AB, nimeltään C, joka on juuri köyden pituus.

On välttämätöntä piirtää C -köyttä kohtisuorassa oleva viiva puoleen kulmassa θ, joka on kahden radion välillä ja jonka kärkipiste on keskusta tai ympärysmitta. Tämä on keskikulma -Koska sen kärki on keskusta ja puolustajaviiva on myös ympärysmitta.

Se voi palvella sinua: radikaalit ominaisuudet

Välittömästi muodostuu kaksi suorakulmiota, joiden hypotenuse. Koska puolustaja ja halkaisija jakautuu kahteen osaan kuin köyttä, osoittautuu, että yksi jaloista on puolet C: stä, kuten kuvassa 3B on osoitettu.

Kulman rinnan määritelmästä:

sin (θ/2) = vastakkainen/hypotenusa cateto = (c/2)/r

Siksi:

sin (θ/2) = c/2r

C = 2R Sen (θ/2)

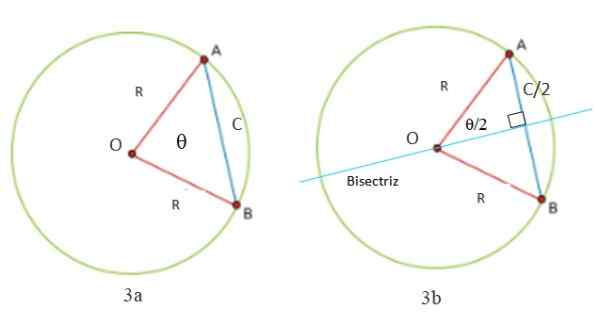Kuva 3. Kahden radion ja kehän köyden muodostama kolmio on sammal (kuva 3), koska sillä on kaksi puolta yhtä suuret. Puolija jakaa sen kahteen suorakulmioon (kuva 3B). Lähde: valmistettu f. Zapata.

Merkkijonolause 

Merkkijonolause sanoo:

Jos jokin kaksi köysiä leikkaa yhdessä pisteessä, yhdelle jousista esiintyvän segmenttien pituuden tuote on yhtä suuri kuin toisessa köydessä määriteltyjen segmenttien pituuksien tuote,.

Seuraava kuva näyttää saman kehän kaksi merkkijonoa: AB ja CD, jotka leikkaavat pisteessä P. AB -köydessä AP- ja PB -segmentit on määritelty, kun taas CP ja PD on määritelty CD -köydessä. Sitten lauseen mukaan:

AP . Pb = cp . P.S

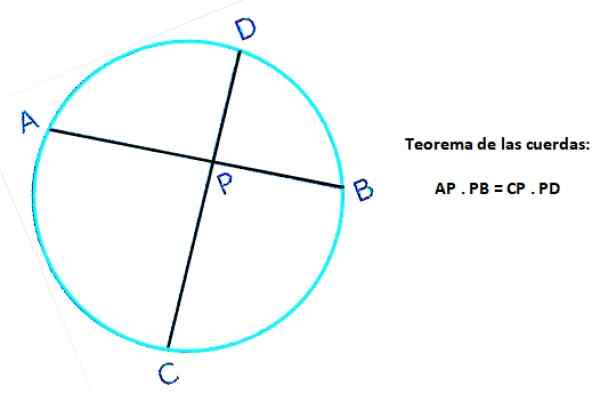Kuva 4. Kehän köysilause. Lähde: f. Zapata.

Ratkaisut jousiharjoitukset

- Harjoitus 1

Ympyrällä on 48 cm: n köysi, joka on 7 cm: n päässä keskustasta. Laske ympyrän pinta -ala ja kehän kehä.

Ratkaisu  

Ympyrän A pinta -alan laskemiseksi riittää, kun tiedät kehän säteen neliölle, koska se täyttyy:

A = π.R -²

Nyt toimitettujen tietojen kanssa muodostettu luku on suorakulmiokolmio, jonka jalat ovat vastaavasti 7 ja 24 cm.

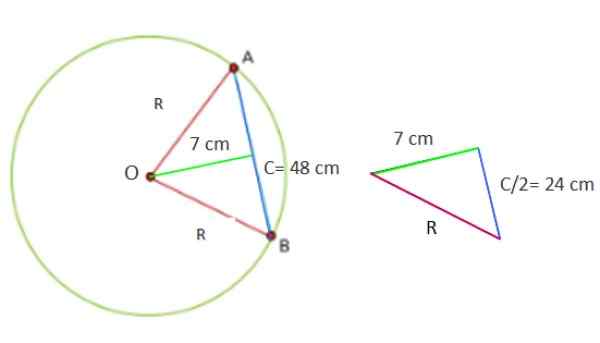Kuva 5. Geometria ratkaistulle harjoitukselle 1. Lähde: f. Zapata.

Siksi R -arvon löytäminen² Pythagoras C -lause sovelletaan suoraan² = a² + b -², Koska r on kolmion hypotenuse:

Voi palvella sinua: NULL Kulma: Määritelmä ja ominaisuudet, esimerkit, harjoitukset

R -² = (7 cm)² + (24 cm)² = 625 cm²

Sitten pyydetty alue on:

A = π. 625 cm² = 1963.5 cm²

Mitä ympärysmitta tai ympärysmitta L: n kehä tai pituus L lasketaan:

L = 2π. R -

Arvojen korvaaminen:

R = √625 cm² = 25 cm

L = 2π. 25 cm = 157.1 cm.

- Harjoitus 2

Määritä ympyrän köyden pituus, jonka yhtälö on:

x² + ja² - 6x - 14y -111 = 0

On tiedossa, että köyden keskipisteen koordinaatit ovat P (17/2; 7/2).

Ratkaisu

P -köyden keskipiste ei kuulu ympärysmittaan, vaan köyden äärimmäiset kohdat Kyllä. Ongelma voidaan ratkaista aiemmin ilmoitetulla jouslauseella, mutta ensin se on kätevä.

Vaihe 1: Hanki kehän kanoninen yhtälö

Ympyrän kanoninen yhtälö keskuksen kanssa (H, K) on:

(X-H)² + (Y-K)² = R²

Sen hankkimiseksi on tarpeen suorittaa neliöt:

(x² - 6x) + (ja² - 14y) -111 = 0

Huomaa, että 6x = 2.(3x) ja 14y = 2.(7y), niin että edellinen ilmaus kirjoitetaan siten, että se on muuttumaton:

(x² - 6x+3²-3²) + (ja² - 14y+7²-7²) -111 = 0

Ja nyt muistaa merkittävän tuotteen määritelmä (A-B)² = a² - 2AB + B² Se voidaan kirjoittaa:

(X - 3)² - 3² + (ja - 7)² - 7² - 111 = 0

= (x - 3)² + (ja - 7)² = 111 + 3² + 7² → (x - 3)² + (ja - 7)² = 169

Ympäristöllä on keskipiste (3,7) ja radio r = √169 = 13. Seuraava kuva näyttää kehän kuvaajan ja lauseessa käytettävät jouset:

Voi palvella sinua: mitkä ovat kehän 7 elementtiä?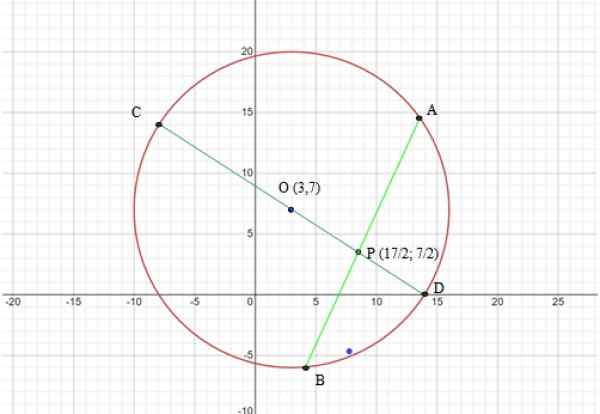Kuva 6. Kaavio harjoituksen ympärysmitasta ratkaistu 2. Lähde: f. Zapata online -graafisen laskimen Mathwayn kautta.

Vaihe 2: Määritä merkkijonolauseessa käytettävät segmentit

Käytettävät segmentit ovat kuvion 6 mukaan CD- ja AB -jouset, molemmat leikataan kohtaan P, siksi:

CP . PD = AP. Pb

Nyt löydämme etäisyyden pisteiden O ja P välillä, koska tämä antaa meille OP -segmentin pituuden. Jos lisäämme säteen tähän pituuteen, meillä on CP -segmentti.

Etäisyys d_Oppi Kahden koordinaattipisteen välillä (x₁,ja₁) ja (x₂,ja₂) On:

d -d_Oppi² = OP² = (x₂ - x₁-A² + (ja₂ - ja₁-A² = (3- 17/2)² + (7-7/2)² = 121/4 + 49/4 = 170/4

d -d_Oppi = OP = √170 /2

Kaikkien saatujen tulosten ja kaavion avulla rakennamme seuraavan segmenttiluettelon (katso kuva 6):

CO = 13 cm = R

OP = √170 /2 cm

Cp = op + r = 13 + √170 /2 cm

PD = OD - OP = 13 - √170 /2 cm

AP = PB

2.AP = köyden pituus

Korvaa merkkijonolause:

CP . PD = AP . Pb = [(13 +√170 /2) . (13 -√170 /2)] = AP²

[169-170/4] = AP²

253/2 = AP²

AP = √ (253/2)

Köyden pituus on 2.AP = 2 (√253/2) = √506

Voisiko lukija ratkaista ongelman toisella tavalla?

Viitteet

1. Baldor, a. 2004. Litteä ja avaruusgeometria trigonometrialla. Kulttuurjulkaisut S.-Lla. C: n.V. Meksiko.
2. C-K12. Sointu. Toipunut: CK12.org.
3. Escobar, J. Ympärysmitta. Toipunut: matematiikka.sinä.Edu.yhteistyö.
4. Villena, m. Kartiomainen. Haettu osoitteesta: dspace.Espoli.Edu.EY.
5. Wikipedia. Köysi (geometria). Palautettu: on.Wikipedia.org.