Steiner Selityslause, sovellukset, harjoitukset

Hän Steinerin lause, tunnetaan myös rinnakkaisakselin lause, Se mahdollistaa laajennetun rungon hitausmomentin arvioinnin akselin ympärillä, joka on yhdensuuntainen toisen kanssa, joka kulkee esineen massakeskuksen läpi.

Sveitsin matemaattinen löysi sen_Cm esineen hitausmomentti suhteessa akseliin, joka kulkee sen CM- ja I Mass -keskuksen läpi_{z -z} hitausmomentti suhteessa toiseen yhdensuuntaiseen akseliin tähän.

Kuvio 1. Suorakulmainen ovi, joka kytkeytyy sen iliin. Lähde: Pixabay.

Tunnetaan etäisyys d, joka erottaa molemmat akselit että massa M kyseisestä kehosta, inertiamomentti inkognito -akseliin nähden on:

Yllyttää_{z -z} = I_Cm + MD²

Hitaushetki osoittaa, kuinka helppoa on, että esine pyörii tietyn akselin ympäri. Se ei riipu pelkästään kehon rungosta, vaan siitä, miten se on jaettu. Tästä syystä se tunnetaan myös nimellä Kiertohitaus, Yksikkösi kansainvälisessä KG -järjestelmässä . m².

Lause osoittaa, että hitaushetki Yllyttää_{z -z} Se on aina suurempi kuin hitaushetki Yllyttää_Cm määräyksenä M.D -d².

[TOC]

Sovellukset

Koska esine pystyy kiertämään lukuisten akselien ympäri, ja taulukoissa yleensä vain hitausmomentti akselia, joka kulkee keskikohdan läpi, Steinerin lause helpottaa laskelmaa, kun sen on pyörittävä akselien akselien runkoja, jotka eivät ole samanaikaisesti kanssa Tämä.

Voi palvella sinua: Strektiliininen liike: Ominaisuudet, tyypit ja esimerkit

Esimerkiksi ovi ei yleensä pyöri akselin ympärillä, joka kulkee sen massan keskuksen läpi, vaan sivuakselin suhteen, missä saranat tarttuvat.

Kun tiedät hitausmomentin, on mahdollista laskea tämän akselin kiertoon liittyvä kineettinen energia. Joo K -k - Onko kineettinen energia, Yllyttää Kyseisen akselin ympärillä oleva hitaushetki ja Ω Kulmanopeus toteutetaan, että:

K = ½ i.Ω²

Tämä yhtälö on hyvin samanlainen kuin massaobjektin hyvin tuttu kineettisen energian kaava M liikkua nopeudella v-  K = ½ m.v². Ja onko hitaus- tai kiertohitaushetki Yllyttää on pyörimässä sama rooli kuin taikina M Käännöksessä.

Steiner -lauseen osoittaminen

Laajennetun esineen hitausmomentti määritellään seuraavasti:

I = ∫r -² Dm

Missä Dm Se on ääretön massa- ja r - Se on etäisyys Dm ja kierto -akseli z -z. Kuviossa 2 tämä akseli ylittää massakeskuksen cm, mutta se voi olla kuka tahansa.

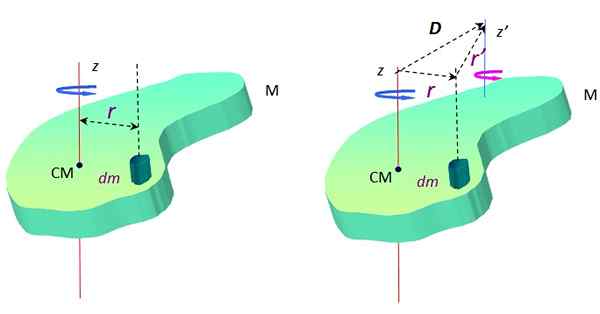Kuva 2. Objekti, joka on laajennettu pyörimään kahden yhdensuuntaisen akselin ympärillä. Lähde: f. Zapata.

Toisen akselin ympärillä  z ', Hitaushetki on:

Yllyttää_{z -z}= ∫ (R ')² Dm

Nyt vektorien muodostaman kolmion mukaan D -d, r - ja R ' (Katso kuva 2 oikealla), on vektorisumma:

r - + R ' = D -d   → R ' = D -d - r -

Kolme vektoria ovat esineen tasossa, jotka voivat olla Xy. Koordinaattijärjestelmän alkuperä (0,0) valitaan CM: ssä seuraavien laskelmien helpottamiseksi.

Tällä tavalla vektorin neliömoduuli R ' On:

Voi palvella sinua: Biofysiikka: historia, mitkä tutkimukset, sovellukset, käsitteet, menetelmät

(R ')² = (D_x- r -_x-A² +(D_ja - r -_ja-A² =

= D_x² + D -d_ja² +r -_x² + r -_ja2 -2d_xr -_x - 2 D_jar -_ja =

= D² + r -²  - 2D_xr -_x - 2 D_jar -_ja

Nyt tämä kehitys korvataan inertia i: n olennaisesti_{z -z} ja myös tiheyden määritelmää DM = ρ.DV:

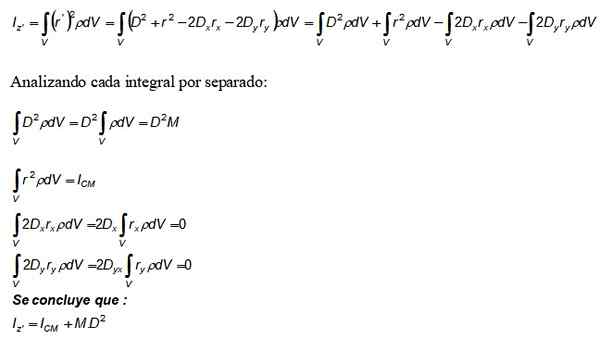
Termi m. D -d² joka esiintyy Steinerin lauseessa, tulee ensimmäisestä integraalista, toinen on hitaushetki akselista, joka kulkee CM: n läpi.

Kolmas ja neljäs integraalit ovat puolestaan ​​0 arvoa, koska määritelmän mukaan ne muodostavat CM: n sijainnin, joka on valittu koordinaattijärjestelmän alkuperä (0,0).

Ratkaisut

-Liikunta ratkaistiin 1

Kuvion 1 suorakulmaisen oven massa on 23 kg, 1,30 leveä ja 2,10 m korkea. Määritä oven hitausmomentti ilon läpi kulkevan akselin suhteen olettaen, että ovi on ohut ja tasainen.

Kuva 3. Esimerkkijärjestelmä ratkaistu 1. Lähde: Muokattu Pixabay.

Ratkaisu

Hitausmomenttipöydältä suorakaiteen muotoiselle levylle massa m ja mitat -lla ja b -, Hitaushetki sen massakeskuksen läpi kulkevan akselin suhteen on: I_Cm = (1/12)M(-lla² + b -²-A.

Oletetaan homogeeninen ovi (lähestymistapa, koska kuvan ovi ei todennäköisesti ole niin paljon). Tässä tapauksessa massan keskus kulkee geometrisen keskuksensa läpi. Kuviossa 3 on piirretty akseli, joka kulkee massan keskuksen läpi ja joka on myös yhdensuuntainen akselin kanssa, joka kulkee ilon läpi.

Yllyttää_Cm = (1/12) x 23 kg x (1.30²+2.10²) m² = 11.7 kg.m²

Voi palvella sinua: mikä on geoidi?

Steinerin lauseen soveltaminen vihreän kierto -akselin kanssa:

I = i_Cm + MD² = 11.7 kg.m² + 23 kg x 0.652 m² = 21.4 kg.

-Liikunta ratkaistiin 2

Löydä ohuen homogeenisen sauvan hitausmomentti, kun se pyörii suhteessa akseliin, joka kulkee yhden sen päistä, katso Kuva. Onko se suurempi vai vähemmän kuin hitausmomentti, kun se pyörii sen keskuksen ympärillä? Koska?

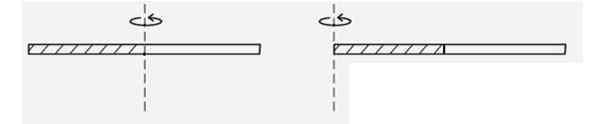Kuva 4. Järjestelmä esimerkkille ratkaistu 2. Lähde: f. Zapata.

Ratkaisu

Hitausmomenttien mukaan hitaushetki Yllyttää_Cm ohut taikinaa M ja pituus Lens On: Yllyttää_Cm = (1/12) ml²

Ja Steinerin lause toteaa, että kun sitä kierretään akselin ympäri, joka kulkee toisen pään läpi d = l/2:

I = i_Cm + MD² = (1/12) ml² + M (l/2)² = (1/3) ml²

Se on vanha.

Etäisyyden vaikutus kierto -akseliin ei ole lineaarinen, vaan neliömäinen. Massa, joka on kaksinkertainen etäisyyteen, että toisella on hitausmomentti verrannollinen (2d)² = 4d².

Viitteet

1. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill. 313-340.
2. Georgian osavaltion yliopisto. Kiertoliike. Toipunut: Phys.Nthu.Edu.Tw.
3. Rinnakkaisakselin lause. Toipunut: Hyperfysiikka.Phy-Astr.GSU.Edu.
4. Rex, a. 2011. Fysiikan perusteet. Pearson. 190-200.
5. Wikipedia. Rinnakkaisakselin lause. Haettu: vuonna.Wikipedia.org