Kolmas termodynamiikan kaavojen laki, yhtälöt, esimerkit

Se Kolmas termodynamiikan laki toteaa, että suljetun termodynaamisen järjestelmän entropia tasapainossa on yleensä minimaalinen ja vakio, koska sen lämpötila lähestyy 0 Kelviniä.

Tämä entropian arvo on riippumaton muun muassa järjestelmämuuttujista (paine tai sovellettu magneettikenttä). Mitä tapahtuu, koska lämpötila on lähempänä 0 K: ta, järjestelmän prosessit lopetetaan ja kuinka entropia on sisäisen sekoituksen mitta, se välttämättä laskeutuu.

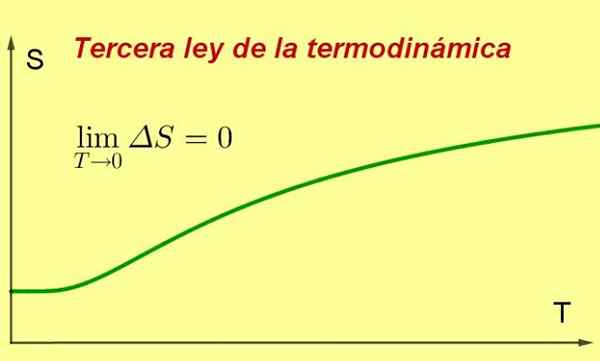
Kuvio 1. Kun järjestelmän lämpötila lähestyy absoluuttista nollaa, sen entropia saavuttaa minimi- ja vakioarvon. Lähde: valmistettu f. Zapata ..

[TOC]

Aikaisemmat käsitteet

Ymmärtääksesi termodynamiikan kolmannen lain laajuuden, joka on merkityksellinen erittäin alhaisissa lämpötiloissa, on tarpeen tarkistaa seuraavat käsitteet:

Termodynaaminen järjestelmä

Se viittaa yleensä kaasuun, nesteeseen tai kiinteään. Mikä ei ole osa järjestelmää, kutsutaan noin. Yleisin termodynaaminen järjestelmä on ihanteellinen kaasu, joka koostuu N -hiukkasista (atomit), jotka ovat vuorovaikutuksessa vain joustavien törmäysten kautta.

Eristetyt, suljetut tai avoimet järjestelmät

Eristettyjä järjestelmiä ei sallita vaihtoa ympäristön kanssa. Suljetut järjestelmät eivät vaihda asiaa ympäristön kanssa, vaan lämpöä. Lopuksi, avoimet järjestelmät voivat vaihtaa sekä aineita että lämpöä ympäristön kanssa.

Makrovaltio ja mikrotila

Järjestelmän makrovaltio on arvot, joilla on muuttujat: paine, lämpötila, tilavuus, moolien lukumäärä, entropia ja sisäinen energia. Toisaalta mikro -esteem -ihanteellisen kaasun tapauksessa -on annettu kunkin N -hiukkasen sijainti ja vauhti, jotka tekevät siitä tietyssä hetkessä. 

Monet mikrovaltiot voivat johtaa samaan makrovaltioon. Huoneen lämpötilan kaasussa mahdollisten mikrovalmisteiden lukumäärä on valtava, koska sen valmistavien hiukkasten lukumäärä, erilaiset asennot ja niiden käyttämät erilaiset energiat ovat erittäin suuria. 

Kaavat ja yhtälöt

Entropia, kuten totesimme, on termodynaaminen makroskooppinen muuttuja, joka mittaa järjestelmän molekyylihäiriön järjestelmää. Järjestelmän häiriöaste on suurempi siinä määrin, että mahdollisten mikrovalmisteiden lukumäärä on suurempi. 

Tätä käsitettä tarvitaan termodynamiikan kolmannen lain laatimiseksi matemaattisessa muodossa. Olipa sitten järjestelmän entropia, sitten:

Tämä tarkoittaa, että suljetun järjestelmän entropia s ei muutu, kun sen lämpötila T yleensä absoluuttinen nolla.

Entropia on makroskooppinen tilamuuttuja, joka liittyy suoraan järjestelmän mahdollisen mikro -arvon lukumäärään seuraavan kaavan avulla:

S = k ln (w)

Edellisessä yhtälössä: S edustaa entropiaa, W - järjestelmän mahdollisten mikro -arvojen lukumäärä ja k -k - Se on Boltzmannin vakio (K = 1.38 x 10^-23 J/k-A. Eli järjestelmän entropia on k -k - kertaa mahdollisten mikrovalmisteiden lukumäärän luonnollinen logaritmi.

Aineen absoluuttisen entropian laskeminen

Puhtaan aineen absoluuttinen entropia on mahdollista määritellä entropian variaation määritelmän perusteella:

Missä ΔQ on lämmön ja T: n äärettömän pienen variaatio on lämpötila. Tämä yhtälö on pätevä, jos prosessi on palautuva (Rev).Jos se on isobarinen - vakiopaineprosessi, äärettömän lämpötilan vaihtelun aikana vaihdettu lämpö voidaan kirjoittaa näin:

ΔQ = n . c_p .DT

Tässä CP on erityinen molaarinen lämpö ja n moolien lukumäärä. Molaarispesifinen lämpöriippu lämpötilaan on kokeellisesti saatu tosiasia ja tunnetaan monista puhtaista aineista.

Voi palvella sinua: aurinkojärjestelmä: planeetat, ominaisuudet, alkuperä, evoluutio

Puhtaiden aineiden kolmannen lain mukaan: 

Joten absoluuttinen entropia puhdasta ainetta, kuten:

Edellisessä merkinnässä palkki osoittaa, että se on aineen moolin entropia ja superson º tarkoittaa puhdasta ainetta.

Sovellukset

Jokapäiväisessä elämässä kolmannella termodynamiikassa on vähän sovelluksia, aivan vastakohtana ensimmäisen ja toisen lain kanssa. Se johtuu siitä, että se on periaate, joka viittaa siihen, mitä järjestelmässä tapahtuu, kun se lähestyy absoluuttista 0, harvinaisten lämpötilojen sijoitus.

Itse asiassa saavuta absoluuttinen tai −273,15 ° C on mahdotonta (ks. Esimerkki 1 myöhemmin), kuitenkin kolmannen lakia sovelletaan tutkittaessa materiaalien vastetta erittäin alhaisissa lämpötiloissa. 

Tämän ansiosta on syntynyt tärkeitä edistysaskeleita kondensoituneessa aineessa, kuten:

-Superfluiditeetti (katso esimerkki 2 myöhemmin)

-Suprajohtavuus 

-Laserjäähdytystekniikat 

-Bose-Einstein-kondensaatti 

-Fermi tarpeeton kaasu.

Kuva 2. Tarpeeton nestemäinen helium. Lähde: Wikimedia Commons.

Erittäin alhaisissa lämpötiloissa entropian laskeutuminen mahdollistaa mielenkiintoisten kvanttien ilmiön syntymisen. Siksi katsotaan, mitä tapahtuu erittäin matalan lämpötilajärjestelmän entropialla.

Matalan lämpötilan järjestelmän entropia

Kun sinulla on täydellinen kiteinen aine, sen minimi entropia on täsmälleen nolla, koska se on erittäin siisti. Absoluuttisen 0 lämpötiloissa aine on tiivistyneessä tilassa (nestemäinen tai kiinteä) ja lasin värähtelyt ovat minimaalisia.

Jotkut kirjoittajat pitävät seuraavan termodynamiikan kolmannen lainsäädännön vaihtoehtoista lausuntoa:

"Jos aine tiivistyy täydellisen kideen muodostaen, kun lämpötila pyrkii absoluuttiseen nollaan, entropialla on taipumus tarkalleen nollaan". 

Tärkeitämme edellisen lausunnon joitain näkökohtia: 

- Täydellinen kide on sellainen, jossa kukin molekyyli on identtinen ja jossa molekyylirakenne toistetaan identtisesti kokonaisuudessaan.

- Koska lämpötila pyrkii absoluuttiseen nollaon, atomivärähtely vähenee melkein kokonaan.

Sitten lasi muodostaa yhden mahdollisen kokoonpanon tai mikroasennuksen, toisin sanoen W = 1, Ja siksi entropia on yhtä suuri kuin nolla:

 S = k ln (1) = 0

Mutta ei niin kauan kuin absoluuttisen nollan lähellä jäähdytetty materiaali muodostaa kristallin, paljon vähemmän tämä kide on täydellinen. Tämä tapahtuu vain, jos jäähdytysprosessi on erittäin hidas ja palautuva.

Muutoin tekijät, kuten lasissa olevat epäpuhtaudet, tekisivät mahdolliseksi muiden mikrovalmisteiden olemassaolon. Siksi w> 1 ja entropia olisi suurempi kuin 0.

Jäännös entropia

Jos jäähdytysprosessi on äkillinen, järjestelmä kulkee saman kuin ei -tasapainotilojen peräkkäin, mikä johtaa materiaaliin näytettäväksi. Tässä tapauksessa ei ole kiteistä ja järjestettyä rakennetta, vaan amorfista kiinteää ainetta, jonka rakenne on samanlainen kuin nesteen rakenne. 

Tällöin absoluuttisen nollan lähellä oleva entropian arvo ei ole nolla, koska mikrotuotteiden lukumäärä on paljon suurempi kuin 1. Ero tämän entropian ja täydellisen kiteisen tilan nolla -entropian välillä tunnetaan nimellä jäännös entropia.

Selitys on, että tietyn kynnyslämpötilan alapuolella järjestelmällä ei ole muuta mahdollisuutta kuin Occupy.

Se voi palvella sinua: Termodynamiikan ensimmäinen laki: kaavat, yhtälöt, esimerkit

He ovat vastuussa jatkuvan entropian ylläpidosta, vaikka lämpötila laskeutuu edelleen absoluuttiseen nollaan.

Esimerkit

Esimerkki 1: Heisenbergin absoluuttinen nolla ja määrittelemätön

Heisenbergin määrittelemättömyyden periaate osoittaa, että hiukkasen aseman ja vauhdin epävarmuus, esimerkiksi kiteisen verkon atomeissa, eivät ole toisistaan ​​riippumattomia, vaan seuraavat seuraavaa eriarvoisuutta:

Δx ⋅ Δp ≥ H

Missä H on Planckin vakio. Eli aseman epävarmuus, joka kerrotaan epävarmuudella vauhdissa (massa nopeutta kohti) on suurempi tai yhtä suuri kuin Planck -vakio, jonka arvo on hyvin pieni, mutta ei nolla: H = 6.63 x 10-3. 4 J · s.

Ja mitä epävarmuuden periaatteella on tekemistä termodynamiikan kolmannen lain kanssa? Jos kiteisen verkon atomien sijainti on kiinteä ja tarkka (Δx = 0) Sitten näiden atomien nopeus voi ottaa minkä tahansa arvon välillä 0 ja äärettömyys. Tätä on ristiriidassa se, että absoluuttisessa nollassa jokainen lämmön levottomuuden liike lakkaa.

Vastavuoroisesti, jos aloitamme sen absoluuttisessa lämpötilan nollassa, kaikki levottomuus lakkaa ja verkon kunkin atomin vauhti on täsmälleen nolla (ΔP = 0), sitten Heisenbergin epävarmuusperiaate viittaa siihen, että kunkin atomin asemien määrittelemätön olisi ääretön, ts. Ne voivat olla missä tahansa asennossa. 

Edellisen lausunnon seurauksena mikrovalmisteiden lukumäärällä on taipumus äärettömyyteen ja entropia ottaisi myös määrittelemättömän arvon. 

Esimerkki 2: Ylivoimaisuus ja helium-4: n outo tapaus

Tarpeettomuudessa, jota esiintyy erittäin alhaisissa lämpötiloissa, aine menettää sisäisen kitkan sen molekyylien välillä, joita kutsutaan goo. Tässä tapauksessa neste voi kiertää ilman kitkaa ikuisesti, mutta ongelma on näissä lämpötiloissa melkein mikään ei ole nestettä paitsi helium.

Helium ja helium 4 (sen runsain isotooppi) muodostavat ainutlaatuisen tapauksen, koska ilmakehän paineessa ja lämpötiloissa lähellä absoluuttista nollaa helium pysyy nesteessä. 

Kun helium-4 toimitetaan lämpötilassa alle 2.2 K ilmakehän paineessa tulee a tarpeeton. Tämä löytö tapahtui vuonna 1911 Hollantilaisen fyysikon Heike Kamerlingh Onnesin Leydenissä (1853-1926).

Kuva 3. Hollantilainen fyysikko Heike Kamerlingh Ones (1853-1926). Lähde: Wikimedia Commons.

Helio-4-atomi on a Bosón. Bosonit, toisin kuin fermionit, ovat hiukkasia, jotka voivat miehittää kaiken saman kvanttitilan. Siksi luut eivät täytä Paulin syrjäytymisperiaatetta.

Sitten kaikki helium-4-atomit lämpötiloissa alle 2.2 K miehittää saman kvanttitilan, ja siksi ei ole muuta kuin yksi mahdollista mikromia, mikä tarkoittaa, että tarpeeton helium-4 on S = 0.

Ratkaisut

- Harjoitus 1

Harkitse yksinkertaista tapausta, joka koostuu järjestelmästä, jonka muodostavat vain kolme hiukkasia, joilla on kolme energiatasoa. Tätä yksinkertaista järjestelmää varten:

a) Määritä mikromäärän lukumäärä, joka on mahdollista kolmelle lämpötila -alueelle:

-korkea 

-Puoli 

-Matala

b) Määritä Boltzmann -yhtälön entropian kautta eri lämpötila -alueilla. 

c) Keskustele tuloksista ja selitä, onko termodynamiikan kolmannen lain kanssa ristiriitainen vai ei.

Liittää jhk

Molekyyli- ja atomi -asteikolla järjestelmän käyttöönotto energiat kvantisoivat, mikä tarkoittaa, että vain tietyt erilliset arvot voivat ottaa. Lisäksi, kun lämpötilat ovat niin alhaiset, järjestelmän muodostavilla hiukkasilla on vain mahdollisuus käyttää vähemmän energiatasoja. 

Se voi palvella sinua: magneettinen induktio: kaavat, miten se lasketaan ja esimerkkejä

Korkea lämpötila

Jos järjestelmässä on suhteellisen korkea lämpötila, hiukkasilla on tarpeeksi energiaa käyttää käytettävissä olevia tasoja, jolloin saadaan 10 mahdollista mikrotuotteita, jotka näkyvät seuraavassa kuvassa:

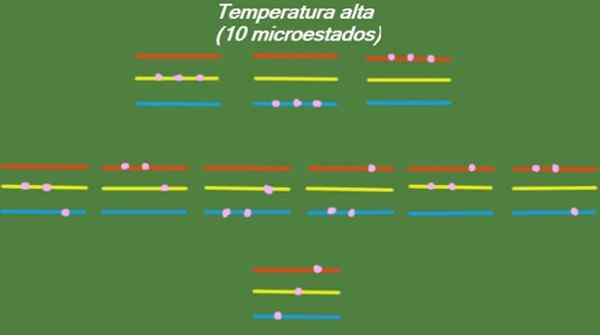Kuva 4. Mahdolliset tilat korkeassa lämpötilassa vuodelle ratkaistiin 1. Lähde: valmistettu f. Zapata.

Keskilämpötila

Jos järjestelmällä on välilämpötila, silloin hiukkasilla, jotka tekevät siitä. Mahdolliset mikro -arvot on havainnollistettu kuvassa:

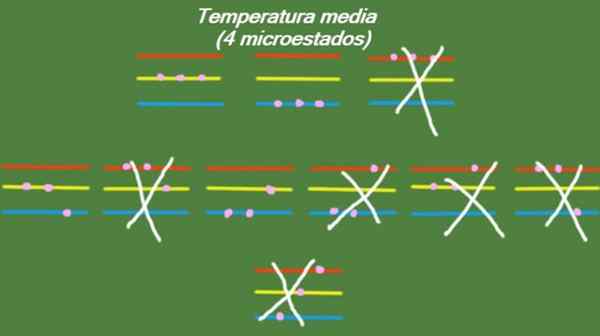Kuva 5. Mikrovaltiossa keskilämpötilassa ratkaistulle liikuntajärjestelmälle 1. Lähde: valmistettu f. Zapata.

Matala lämpötila

Jos lämpötila laskeutuu edelleen idealisoidussa kolmessa hiukkasessa ja kolmessa energiatasossa, hiukkasilla on niin vähän energiaa, että ne voivat vain käyttää alhaisinta tasoa. Tässä tapauksessa on vain yksi mahdollista mikrovaltaa, kuten kuvasta 6 voidaan nähdä:

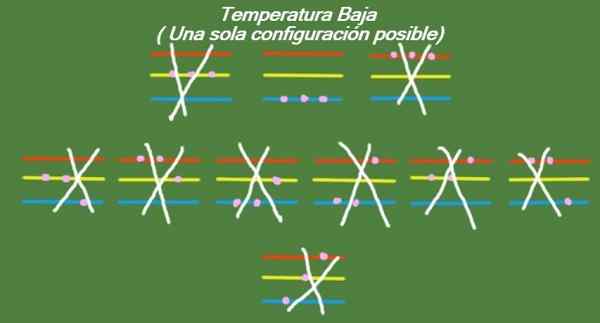Kuva 6. Matalassa lämpötilassa on mahdollista kokoonpanoa (oma yksityiskohta)

Ratkaisu b

Tietävät jo mikrotuotteiden lukumäärän kussakin lämpötila -alueella, voimme jo käyttää Boltzmann -yhtälöä, joka on aikaisemmin annettu entropian löytämiseksi kussakin tapauksessa.

S = k ln (10) = 2.30 x k = 3.18 x 10-23 J/k (Korkea lämpötila)

S = k ln (4) = 1.38 x K = 1.92 x 10-23 J/k (Keskilämpötila)

Ja lopuksi:

S = k ln (1) = 0 (Matala lämpötila)

Liuos C

Ensinnäkin huomaamme, että entropia laskee lämpötilan laskeutuessa, kuten odotettiin. Mutta alhaisimmille lämpötila -arvoille saavutetaan kynnysarvo, josta järjestelmän perustila saavutetaan.

Vaikka lämpötila on mahdollisimman lähellä absoluuttista nollaa, ei ole käytettävissä pienempiä tiloja. Sitten entropia ylläpitää vakiona minimiarvoaan, joka esimerkissämme on s = 0.

Tämä harjoitus kuvaa järjestelmän mikrotuotteiden tasolla syytä, miksi termodynamiikan kolmas laki täyttyy.

- Harjoitus 2

Syy, jos seuraava lausunto on totta tai väärä:

"Järjestelmän entropia absoluuttisessa lämpötilassa nolla on täsmälleen nolla".

Perustele vastaus ja kuvaile joitain esimerkkejä.

Ratkaisu

Vastaus on: väärä.

Ensinnäkin absoluuttista lämpötilaa ei voida saavuttaa, koska Heisenbergin epävarmuuden periaate ja termodynamiikan kolmas laki loukataan. 

On erittäin tärkeää huomata, että kolmannessa laissa ei sanota, mitä tapahtuu absoluuttisessa 0, mutta kun lämpötila on äärettömän lähellä absoluuttista 0. Ero on hieno, mutta merkittävä.

Kolmas laki ei väitä, että kun lämpötila ottaa arvon mielivaltaisesti lähellä absoluuttista nollaa, entropialla on taipumus nolla. Tämä tapahtuisi vain aiemmin analysoidussa tapauksessa: täydellinen kide, joka on idealisointi.

Monilla mikroskooppisten asteikkojen järjestelmillä, toisin sanoen kvanttiasteikolla, on energiapohjataso rappeutua, Mikä tarkoittaa useiden kokoonpanojen olemassaoloa alimmalla energiatasolla. 

Yllä oleva tarkoittaa, että näissä järjestelmissä entropia ei koskaan olisi tarkalleen nolla. Entropia ei myöskään ole tarkalleen nolla järjestelmissä, jotka ovat lasitettuja, kun lämpötila pyrkii absoluuttiseen nolla. Tässä tapauksessa jäännös entropia Ennen nähtyä.

Se johtuu siitä, että heidän molekyylit olivat "jumissa" ennen kuin he käyttävät alhaisinta käytettävissä olevaa energiatasoa, mikä lisää huomattavasti mahdollisten mikro -arvon määrää, mikä tekee mahdottomaksi, että entropia on täsmälleen nolla.

Viitteet

1. Cengel, ja. 2012. Termodynamiikka. 7. painos. McGraw Hill. 347.
2. Jet Propulsion Laboratory. Maailmankaikkeuden tyylikkäin paikka. Toipunut: ColdatomLab.JPL.potti.Hallitus.
3. González, a. Entropia ja spontaanisuus. Toipunut: Geocityt.WS
4. QUORA. Mikä on termodynamiikan kolmannen lain käytännöllinen käyttö?. Palautettu: Quora.com
5. Yleinen kemia. Kolmas termodynamiikan periaate. Toipunut: Korintti.PUCP.Edu.PE -PE
6. Kolmas termodynamiikan laki. Palautettu: YouTube.com
7. Wikipedia. Entropian jäännös. Haettu: vuonna.Wikipedia.com
8. Wikipedia. Kolmas termodynamiikan laki. Haettu: vuonna.Wikipedia.com