Newtonin kolmas lakihakemukset, kokeet ja harjoitukset

Se Newtonin kolmas laki, kutsutaan myös Toimintalaki ja reaktio Hän väittää, että kun esine käyttää voimaa toiseen, jälkimmäinen käyttää myös ensimmäisellä suuruudella ja suuntaisella ja vastakkaisella merkityksellä.

Isaac Newton julkaisi kolme lakia vuonna 1686 kirjassaan Filosophiae naturalis Principia Mathematica tai luonnonfilosofian matemaattiset periaatteet.

Avaruusraketti saa tarvittavan työntövoiman karkotettujen kaasujen ansiosta. Lähde: Pixabay.

[TOC]

Selitys ja kaavat

Newtonin kolmannen lain matemaattinen muotoilu on hyvin yksinkertainen:

F₁₂ = -F_{kaksikymmentäyksi}

Yksi joukkoista kutsutaan toiminta Ja toinen on reaktio. Tämän yksityiskohdan merkitys on kuitenkin tarpeen korostaa: molemmat toimivat eri kohteisiin. He tekevät sen myös samanaikaisesti, vaikka tämä terminologia viittaa väärin siihen, että toiminta tapahtuu ennen ja reaktio.

Koska joukot ovat vektoreita, ne merkitään rohkeina. Tämä yhtälö osoittaa, että objektia on kaksi: objekti 1 ja objekti 2. Voima F₁₂ Se käyttää esinettä 1 esineeseen 2. Voima F_{kaksikymmentäyksi} Objekti 2 käyttää objektia 1. Ja merkki (-) huomauttaa, että he ovat vastustaneet.

Kun tarkkaillaan huolellisesti Newtonin kolmatta lakia, on olemassa tärkeä ero kahdessa ensimmäisessä: Vaikka he vetoavat yhteen esineeseen, kolmas laki viittaa kahteen eri esineeseen.

Ja jos ajattelet huolellisesti, vuorovaikutukset vaativat esineiden paria.

Siksi toiminta- ja reaktion voimia ei peruuteta tai tasapainotettu, vaikka niillä on sama suuruus ja suunta, mutta muuten: niitä käytetään eri kappaleissa.

Sovellukset

Pallovuorovaikutus - Maa

Tässä on erittäin päivittäinen sovellus Newtonin kolmanteen lakiin liittyvästä vuorovaikutuksesta: pallo, joka putoaa pystysuunnassa ja maalla. Pallo putoaa maahan, koska maalla on vetovoima, joka tunnetaan nimellä Gravity. Tämä voima aiheuttaa pallon putoamisen jatkuvalla kiihtyvyydellä 9.8 m/s².

Melkein kukaan ei kuitenkaan ajattele sitä, että pallo myös saa vetovoiman maapallolle. Tietysti maa on edelleen muuttumaton, koska sen massa on paljon suurempi kuin pallon massa ja kokee siksi halveksivan kiihtyvyyden.

Toinen huomattava kysymys Newtonin kolmannesta laista on, että kahden vuorovaikutuksen välinen yhteys ei ole välttämätöntä. Se on ilmeistä juuri mainittujen esimerkkien kanssa: pallo ei vieläkään ota yhteyttä maahan, mutta silti se harjoittaa vetovoimaa joka tapauksessa. Ja pallo myös maan päällä.

Painovoima, joka toimii vuorottelevasti, molemmat, jos esineiden välillä on kosketusta ikään kuin "etäisyystoimintavoiman" nimeä ei olisi nimeä. Sen sijaan voimat, kuten kitka ja normaali, he vaativat, että vuorovaikutuksessa olevat esineet ovat kosketuksissa, joten niitä kutsutaan "kontaktiksi".

Esimerkistä uutetut kaavat

Paluu pariin pallo -objektiin - Maa, pallojen P -nopeuden valitseminen ja T: n P -hinnat ja T -järjestelmän toisen lain soveltaminen tämän järjestelmän jokaiselle osallistujalle saadaan:

Se voi palvella sinua: Diskreetti muuttuja: Ominaisuudet ja esimerkit

F_{seurauksena oleva} = m.-lla

Kolmannessa laissa todetaan, että:

m_P-lla_P = - m_T-lla_T

-lla_P = 9.8 m/s² Pystysuoraan suuntautuva. Koska tämä liike tapahtuu pystysuunnassa, voidaan antaa vektorimerkinnällä (lihavoitu); Ja suuntaa suuntaan positiiviseksi ja alaspäin kuin negatiivinen, sinulla on:

-lla_P = 9,8 m/s²

m_T ≈ 6 x 10 ²⁴ Kg

Pallon massasta riippumatta maan kiihtyvyys on nolla. Siksi havaitaan, että pallo putoaa kohti maata eikä päinvastoin.

Raketin toiminta

Raketit ovat hyvä esimerkki Newtonin kolmannen lain soveltamisesta. Kuvassa näkyvä raketti nousee kuuman kaasun työntövoiman ansiosta suurella nopeudella.

Monet uskovat, että näin tapahtuu, koska nämä kaasut "tukevat" ilmakehää tai maassa tukemaan ja työntämään rakettia. Se ei toimi niin.

Kun raketti käyttää voimakkuutta kaasuihin ja karkottaa ne takaisin, kaasut kohdistavat voiman rakettiin, jolla on sama moduuli, mutta vastakkainen suuntaa. Tämä voima tarjoaa raketin kiihtyvyytensä ylöspäin.

Jos sinulla ei ole niistä rakettita käsin, on muita tapoja varmistaa, että Newtonin kolmas laki toimittaa työntövoiman tarjoamiseksi. Vesiä voidaan rakentaa, joihin tarvittava työntövoima tarjoaa vesipainekaasua kohti.

On huomattava, että vesiraketin aloitus vie aikaa ja vaatii monia varotoimenpiteitä.

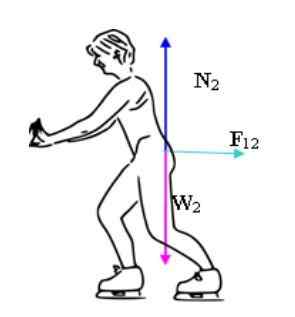
Luistimien käyttö

Edullisempi ja välitön tapa tarkistaa Newtonin kolmannen lain vaikutus on pari luistinta ja seinän mainostaminen.

Suurimman osan ajasta kyky käyttää voimaa liikkeessä olevien esineiden kanssa, mutta totuus on, että liikkumattomat esineet voivat myös käyttää voimaa. Luistelija ajaa takaisin voiman ansiosta, jota liikkumattomat käyttävät siihen.

Kosketuspinnat käyttävät kosketusvoimia (normaali) toistensa kanssa. Kun kirjaa tuetaan vaakasuorassa taulukossa, se käyttää normaalia pystysuoraa voimaa. Kirja käyttää taulukossa saman numeerisen arvon ja vastakkaisen merkityksen pystysuuntaista voimaa.

Lasten kokeilu: luistelijat

Lapset ja aikuiset voivat kokea Newtonin kolmannen lain ja varmistaa, että toiminta- ja reaktiovoimia ei kumota ja kykenevät tarjoamaan liikkeitä.

Kaksi luistelijaa jäällä tai erittäin sileällä pinnalla voidaan ajaa kukin.

Harkitse kahta luistelijaa, joilla on aivan erilainen taikina. He ovat keskellä halveksittavaa kitkaa ja ovat alun perin levossa. Tietyssä hetkessä he työntävät toisiaan levittäen vakiovoimaa kämmenillä. Kuinka molemmat liikkuvat?

Voi palvella sinua: tasapainotusvektori: Laskenta, esimerkit, harjoituksetKaksi luistelijaa on ajautunut keskelle jäähalli. Lähde: Benjamin Crowell (Wikipedia-käyttäjä Bcrowell) [CC BY-SA 3.0 (http: // creativecommons.Org/lisenssit/by-SA/3.0/]]

On tärkeää korostaa, että koska se on pinta ilman kitkaa, ainoat epätasapainoiset voimat ovat voimat, joita luistelijat käyttävät toisiaan. Vaikka paino ja normaali toimivat molemmille, nämä voimat ovat tasapainossa, mitä luistelijat kiihdyvät pystysuunnassa.

Tässä esimerkissä sovelletut kaavat

Newtonin kolmannen lain mukaan:

F₁₂ = -F_{kaksikymmentäyksi}

Toisin sanoen luistelija 1: n 2: een kohdistama voima on sama, jonka kohdalla 2 kohdistaa 1: n, samaan suuntaan ja vastakkaiseen suuntaan. Huomaa, että näitä voimia sovelletaan eri esineisiin, samalla tavalla kuin voimat olivat palloilla ja maalla edellisessä käsitteellisessä esimerkissä.

m₁ -lla₁ = -m₂ -lla₂

Koska voimat ovat päinvastaisia, myös aiheuttavat kiihtyvyydet ovat, mutta niiden suuruudet ovat erilaisia, koska jokaisella luistelijalla on erilainen massa. Katsotaanpa ensimmäisen luistelijan hankkimaa kiihtyvyyttä:

Jos ensimmäisen luistelijan massa on suurempi kuin toisen, sen kiihtyvyys on alhaisempi. Tätä on odotettavissa, koska sillä on suurempi hitaus. Kevyin luistelija saavuttaa suuremman kiihtyvyyden. Jos massot ovat samat, myös kiihtyvyydet ovat.

Joten alla tapahtuva liike on molempien luistelijoiden erottaminen vastakkaisissa aisteissa. Periaatteessa luistelijat olivat levossa radan keskellä. Jokaisella on voiman toiseen, joka tarjoaa kiihtyvyyden kätensä ollessa kosketuksessa ja työntövoima kestää.

Sen jälkeen luistelijat siirtyvät toisistaan ​​yhtenäisellä suorakulmaisella liikkeellä, koska ne eivät toimisi epätasapainoisia voimia. Kunkin luistelijan nopeus on erilainen, jos myös niiden massot ovat.

Liikuntaa

Ratkaisemaan ongelmia, joissa Newtonin lakeja on sovellettava, on tarpeen piirtää huolellisesti esineeseen toimivia voimia. Tätä piirustusta kutsutaan "vapaa kehon kaavio" tai "eristetty kehon kaavio". Tässä kaaviossa voimat, joita vartalo käyttää muita esineitä, ei tule näyttää.

Jos ongelmaan osallistuu enemmän kuin yksi esine, se on välttämätöntä.

1- Edellisen osan luistelijoilla on vastaavat massot m₁ = 50 kg ja m₂ = 80 kg. He työntävät toisiaan jatkuvalla 200 N: n voimalla. Työntövoiman kesto on 0.40 sekuntia. Löytö:

a) Kunkin luistelijan hankkima kiihtyvyys työntövoiman ansiosta.

b) kunkin nopeus, kun ne erottuvat

Ratkaisu

a) Ota vaakasuora positiivinen osoite, joka menee vasemmalta oikealle. Newtonin toisen lain soveltaminen lausunnon antamiin arvoihin on:

F_{kaksikymmentäyksi} = m₁-lla₁

Mistä:

Toiselle luistelijalle:

b) Laskea nopeus, jota he kuljettavat erikseen, käytetään tasaisesti kiihdytetyn suoraviivaisen liikkeen kinemaattisia yhtälöitä:

Voi palvella sinua: keskinäinen induktanssi: kaava/kerroin, sovellukset, harjoitukset

Alkuperäinen nopeus on 0, koska ne olivat levossa radan keskellä:

v_F =

v_F1 = a₁t = -4 m/s² . 0 -.40 s = -1.6 m/s

v_F2 = a₂T = +2.5 m/s² . 0 -.40 s = +1 m/s

Tulokset

Kuten odotettiin, henkilö 1 on kevyempi saavuttaa suuremman kiihtyvyyden ja siten nopeamman nopeuden. Tarkkaile nyt seuraavaa taikinan tuotteesta kunkin luistelijan nopeuden vuoksi:

m₁ v₁ = 50 kg . (-1.6 m/s) = - 80 kg.neiti

m₂ v₂ = 80 kg . 1 m/s = +80 kg.neiti

Molempien tuotteiden summa on 0. Massan tuotetta nopeudella kutsutaan liikkeen p: ksi. Se on vektori, jolla on sama suunta ja nopeus. Kun luistelijat olivat levossa ja heidän kätensä kosketuksessa, voitiin olettaa, että he muodostivat saman esineen, jonka liikkeen määrä oli:

P_jompikumpi = (m₁ +m₂) v_jompikumpi = 0

Kun työntövoima on valmis, luistelujärjestelmän liikkumisen määrä pysyy 0. Siksi liikkeen määrä säilyy.

Esimerkkejä Newtonin kolmannesta laista jokapäiväisessä elämässä

Kävellä

Kävely on yksi päivittäisimmistä toimista, joita voidaan suorittaa. Jos tarkkaillaan huolellisesti, kävelytoimenpide vaatii jalan työntämistä maahan, niin että se palauttaa saman ja vastakkaisen voiman kävelijän jalkaan.

Kun sovelsimme jatkuvasti Newtonin kolmatta lakia. Lähde: Pixabay.

Juuri se voima antaa ihmisille mahdollisuuden kävellä. Lennolla linnut käyttävät voimaa ilmassa ja ilma työntää siipiä siten, että lintu ajaa eteenpäin.

Auton liike

Autossa pyörillä on vahvuus jalkakäytävälle. Jalkakäytäväreaktion ansiosta se käyttää rengasvoimia, jotka ajavat autoa eteenpäin.

Urheilu

Urheilukäytännössä toiminta- ja reaktiovoimat ovat lukuisia, ja heillä on erittäin aktiivinen osallistuminen.

Esimerkiksi, katsotaan urheilija, jolla on aloituslohko tukee jalkaa. Lohko tarjoaa normaalin voiman reaktiona työntekijän käyttämälle työntövoimalle. Tämän normaalin ja käytävän painon tulos johtaa vaakasuoraan voimaan, joka antaa urheilijan ajaa eteenpäin.

Urheilija käyttää käynnistyslohkoa lisäämään impulssia eteenpäin lähtöön. Lähde: Pixabay.

Paloletku

Toinen esimerkki, jossa Newtonin kolmas laki on läsnä, on palomiehissä, jotka pitävät paloletkiä. Näiden suurten letkujen lopussa on suuttimessa kahva, joka palomiehen on pidettävä, kun vesisuihku tulee ulos, jotta vältetään takaisku.

Samasta syystä se on kätevä.

Viitteet

1. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. Kuudes painos. Prentice Hall. 80 - 82.
2. Rex, a. 2011. Fysiikan perusteet. Pearson. 73 - 75.
3. Tipler, P. 2010. Fyysinen. Osa 1. 5. painos. Toimitus palautti. 94 - 95.
4. Stern, D. 2002. Tähtitieteet astronaveihin. Otettu: PWG.GSFC.potti.Hallitus.