Integraalit
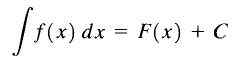
- 2865
- 345
- Sheldon Kuhn
Se Integraalit Se, että olemme laskelmassa, ovat määrittelemättömät integraalit ja määritetyt integraalit. Vaikka määriteltyjen integraalien on paljon enemmän sovelluksia kuin määrittelemättömät integraalit, on ensin tarpeen oppia ratkaisemaan määrittelemättömät integraalit.
Yksi määriteltyjen integraalien houkuttelevimmista sovelluksista on vallankumouksen kiinteän määrän laskeminen. Molemmilla integraalityypeillä on samat lineaarisuusominaisuudet, ja myös integraatiotekniikat eivät riipu integraalin tyypistä.
Mutta huolimatta siitä, että se on hyvin samanlainen, on tärkein ero; Ensimmäisessä integraalityypissä tulos on funktio (joka ei ole spesifinen), kun taas toisessa tyypissä tulos on numero.
Perustyypit integraalit
Integraalien maailma on erittäin laaja, mutta tässä voimme erottaa kaksi integraalityyppiä, joilla on suuri sovellettavuus jokapäiväisessä elämässä.
1- määrittelemättömät integraalit
Jos f '(x) = f (x) kaikille x: lle F: n alueella, sanomme, että f (x) on antidervatiivinen, primitiivinen tai f (x) -yhtiön integraali.
Toisaalta huomataan, että (f (x)+c) '= f' (x) = f (x), mikä tarkoittaa, että funktion integraali ei ole ainutlaatuinen, koska eri arvojen antaminen vakiona C saadaan erilaisia antiDervantiveja.
Tästä syystä f (x)+c kutsutaan F (x): n ja C: n määrittelemättömäksi integraaliksi kutsutaan integraationa ja kirjoitamme sen seuraavasti:
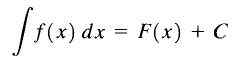 Määrittelemätön integraali
Määrittelemätön integraali Kuten voimme nähdä, funktion f (x) määrittelemätön integraali on funktioiden perhe.
Esimerkiksi, jos haluat laskea funktion f (x) = 3x²: n määrittelemätön integraali, ensin on ensin löydettävä f (x).
Voi palvella sinua: TrinomialOn helppo huomata, että f (x) = x³ on antitutiivinen, koska f '(x) = 3x². Siksi voidaan päätellä
∫f (x) dx = ∫3x²dx = x³+c.
2- Määritetyt integraalit
Olkoon y = f (x) Todellinen funktio jatkuu suljetulla aikavälillä [a, b] ja olla f (x) f (x): n antidervatiivisuus. Sitä kutsutaan F (x): n määriteltyksi integraaliksi rajojen A ja B välillä lukumäärään F (b) -f (a), ja se tarkoittaa seuraavasti:
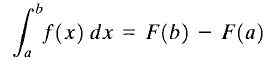 Perustavanlaatuinen laskentalause
Perustavanlaatuinen laskentalause Yllä esitetty kaava tunnetaan paremmin nimellä "laskelman peruslause". Täällä "A" kutsutaan alarajaan ja "B" kutsutaan ylärajaksi. Kuten voidaan nähdä, funktion selvä integraali on numero.
Tässä tapauksessa, jos F (x) = 3x²: n määritelty integraali lasketaan aikavälillä [0,3], lukumäärä saadaan.
Tämän luvun määrittämiseksi valitsemme f (x) = x³ f (x) = 3x². Sitten laskemme F (3) -f (0), joka heittää meidät seurauksena 27-0 = 27. Yhteenvetona voidaan todeta, että F (x): n määritelty integraali aikavälillä [0,3] on 27.
Voidaan huomata, että jos g (x) = x³+3, niin g (x) valitaan, se on f (x): n antipäätoimi, joka on erilainen kuin f (x), mutta tämä ei vaikuta tulokseen g (3) -G (0) = (27+3)-(3) = 27. Tästä syystä määritellyissä integraaleissa integraatiovakio ei näy.
Yksi hyödyllisimmistä sovelluksista, joita tämän tyyppisellä integraalilla on, on se, että se mahdollistaa tasaisen kuvion (kiinteän vallankumouksen) pinta -alan (tilavuuden) laskemisen, riittävien integraatiofunktioiden ja rajojen (ja pyörimisakselin) asettamisen määrittämisen.
Määritettyjen integraalien joukosta löydämme tämän erilaisia laajennuksia, kuten integraalit, pinta -integraalit, väärät integraalit, useita integraaleja, muun muassa erittäin hyödyllisiä sovelluksia tieteessä ja tekniikassa.
Se voi palvella sinua: Ero ympyrän ja kehän välillä (esimerkkien kanssa)Viitteet
- Kishan, H. (2005). Kiinteä laskenta. Atlantin kustantajat ja jakelijat.
- Purcell, E. J -., Varberg, D., & Rigdon, S. JA. (2007). Laskeminen (Yhdeksäs ed.-A. Prentice Hall.

