Kolmiotyypit

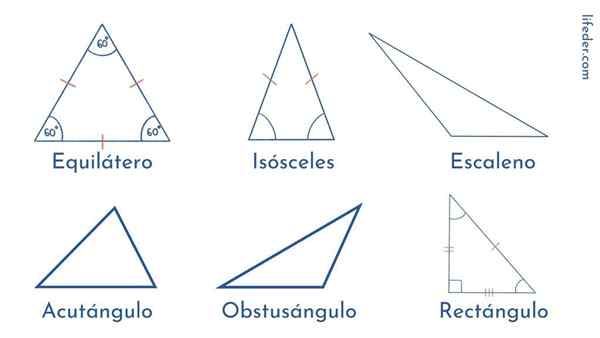Kolmioiden luokittelu

Kolmio on monikulmio- tai geometrinen kuva, jolla on kolme sivua, kolme kärkeä ja kolme kulmaa. Sivut ovat kumpikin suoraa linjaa, jotka muodostavat sen. Verkit ovat pisteitä, joissa sivut liittyvät; Kulmat ovat kaaria tai aukkoja, jotka muodostetaan lähellä kärkipisteitä, liittymällä molemmille puolille.

Kolmio voidaan määritellä myös kolmen rivin määritettynä alueella. Sen kolmen kulman summa on aina yhtä suuri kuin 180º. Minkä tahansa sivun pituus on aina pienempi kuin muiden kahden puolen pituuden summan seuraus, mutta suurempi kuin sen vähennys.

Kolmiot ovat yksinkertaisimpia geometrisia hahmoja, ja niiden tarkoituksena on tutkia muiden monimutkaisempien lukujen, kuten pentagonien tai kuusikulmioiden, matemaattisia ominaisuuksia.

Niitä käytetään myös muissa tieteissä, kuten topografia, navigointi tai tähtitiede. Viimeksi mainitussa heillä on tottunut tietämään etäisyys, joka erottaa meidät kaukaisesta vaaleansinisestä rungosta kahdesta maapallolla sijaitsevasta havaintopisteestä. Tätä menetelmää kutsutaan rinnakkaiseksi.

Kolmiot luokitellaan sivujensa pituuden mukaan tai niiden kulmien amplitudin mukaan.

Kolmiotyypit niiden sivujen mukaan

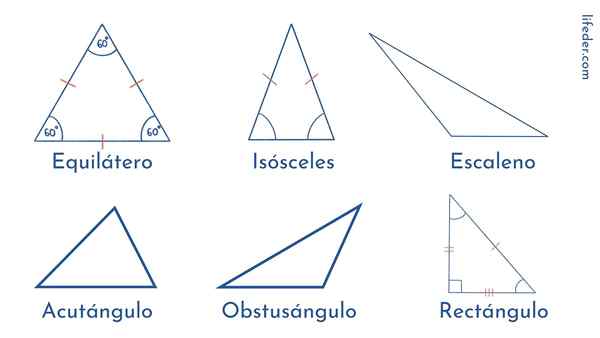
Tasasivuinen kolmio

Tämän tyyppisen kolmion sivuilla on täsmälleen sama pituus. Ja sama koskee heidän kulmiaan: kolme mittaa 60º. Siksi sanomme, että tasapainon kolmio on tavallinen monikulmio.

Skaaleenikolmio

Toisin kuin tasa -arvoinen, skaleenikolmiossa kaikki on epätasaista: sen kolmella sivulla on eri pituudet ja sen kulmat eroavat amplitudista.

Voi palvella sinua: yhdistetyt toiminnot

Tasakylkinen kolmio

Tämän tyyppisessä kolmiossa havaitaan, että kahdella puolella on sama mitta, kun taas jäljellä oleva puoli on erilainen. Sama havaitaan kulmien amplitudissa: kaksi ovat samat ja yksi erilainen.

Kolmiotyypit niiden kulmien mukaan

Suorakulmainen kolmio

Sille on ominaista, että sillä on suorakulma, ts. 90º. Hänen kaksi muuta kulmaa ovat akuutteja tai vähemmän kuin 90º.

Tämän tyyppisissä kolmioissa pisin puoli kutsutaan hypotenusaksi, kun taas toinen kaksi puolta ovat luokkia.

Vino kolmio

Kolmiot, joilla ei ole mitään suorakulmaa, kuuluvat tähän tyyppiin. Ne on jaettu kahteen tyyppiin:

Acutangle -kolmio: Hänen kolme kulmaa ovat akuutteja.

Sotkuinen kolmio: Heillä on kaksi akuuttia kulmaa ja yksi obtualisesti tai suurempi kuin 90º.

Sekoitettu kolmio

Sama kolmio voidaan luokitella kahden kriteerin mukaan, toisin sanoen niiden sivujen pituuden ja heidän kulmien amplitudin mukaan.

Esimerkiksi suorakulmiokolmio voi olla myös Escalano tai ISCELES, mutta se ei voisi olla tasa -arvoinen, koska jälkimmäisessä ei ole mitään suorakulmaa.

Tasasivuinen kolmio voi kuitenkin olla akuutti, koska siinä on tehokkaasti kolme akuuttia tai vähemmän kuin 90º kulmaa.

Scalene foluse -kolmio

Skaleenikolmio voidaan olla tehokkaasti, koska sen kulmien sekä sen amplitudi että sen sivujen pituus ovat erilaisia.

Kuinka laskea kolmion kehä?

Kolmion kolmen sivun pituuden summan tuotetta kutsutaan kehäksi.

Katsotaanpa joitain esimerkkejä.

1- Meitä pyydetään löytämään skaleenikolmion kehä, jonka sivut 6, 8 ja 4 senttimetriä. Meidän on vain lisättävä:

Voi palvella sinua: Absoluuttinen vakio

6 + 8 + 4 = 18

Siksi tämän skaleenikolmion kehä on 10 senttimetriä.

2- Sitten he pyytävät meitä laskemaan tasavirta kolmion kehä, jonka sivut mittaavat 4 senttimetriä kaksi ja 6 senttimetriä jäljellä oleva puoli. Koska kahdella sivulla on sama pituus, meidän on asetettava sama kuva kahdesti, kuten tämä:

4 + 4 + 6 = 14

Tämän kolmion kehä on 14 senttimetriä.

3- Viimeinen esimerkki. Meillä on tehtävä määrittää 9 senttimetrin tasapainon kolmion kehä sivuttain. Kuten tiedämme erityyppisten kolmioiden ominaisuudet, tiedämme. Siksi:

9 + 9 + 9 = 27

Tämän tasapainon kehä on 27 senttimetriä.

Mediatrices, Piisektorit ja keskipitkä

Nämä ovat kolmen tyyppisiä suoria viivoja, jotka voidaan piirtää kolmioon.

Välittäjä

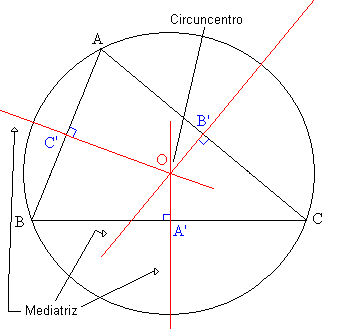
On kolme, yksi kolmion molemmilla puolilla. Mediatrix on suora viiva, joka kulkee kolmion puolen keskipisteen läpi, jota se vastaa. Kolmion kolme mediatrista leikkaavat pisteessä, joka tunnetaan nimellä Ympärercentro, joka on samassa etäisyydellä kunkin kolmion kärkipisteestä.

Puolustajat

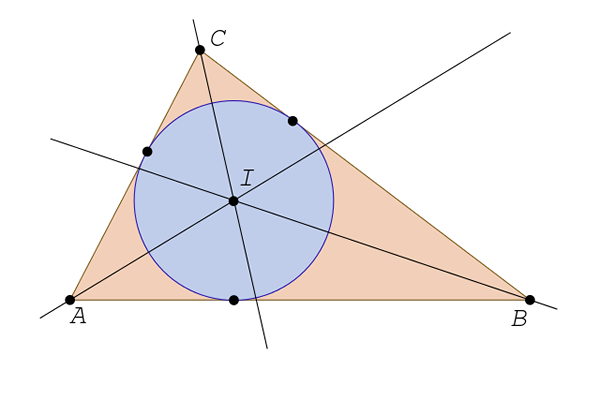
Jokaista kulmaa on kolme, yksi. Puoli on suora viiva, joka alkaa kärkipisteestä ja jakaa kulman kahteen yhtä suureen osaan. Kolmion puoliajat leikkaavat kohtaan, joka tunnetaan nimellä kannustin.

Keskipitkä

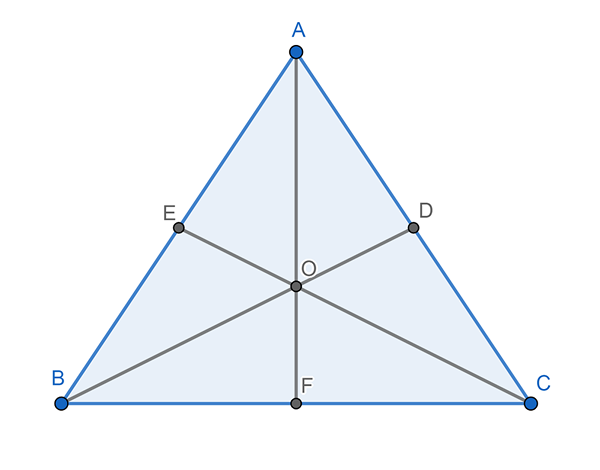
Jokaista kärkipistettä on myös kolme, yksi. Mediaani on linja, joka alkaa kärkipisteestä ja saavuttaa keskipisteen vastakkaisella puolella. Kolmion mediaanit leikkaavat pisteessä nimeltään Baricentro.

Voi palvella sinua: näytteenottovirhe: kaavat ja yhtälöt, laskenta, esimerkit

Etäisyys minkä tahansa kolmen kärjen ja barycenterin välillä vastaa kahta kolmasosaa (2/3) vastaavan mediaanin kokonaispituudesta. Esimerkiksi, jos mediaanin CE mittaa 5 senttimetriä, niin etäisyys C: n ja baricenterin (O) välillä on yhtä suuri 5 x 2/3 tai mikä on sama, 5 x 0,66, mikä johtaa 3, 3 senttimetriin.

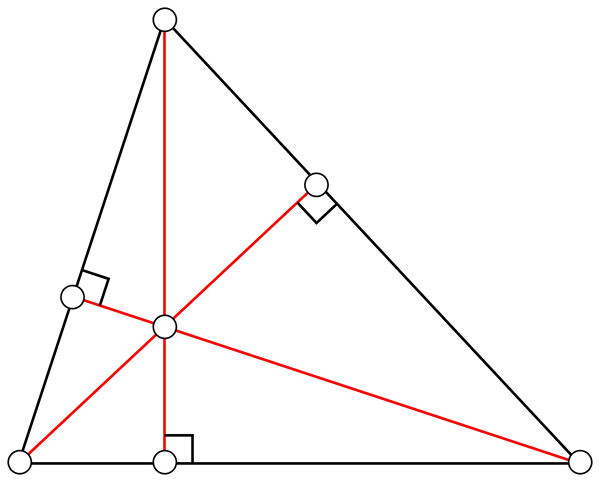
Korkeus

Se on suora viiva, joka liittyy kärkipisteeseen vastakkaisella puolella. Kolme kolmion korkeutta leikkaavat pisteessä, jota kutsutaan ortotroenteriksi. Kolmion tyypistä riippuen ortokeskuksessa voi olla kolmion alueen sisällä tai sen ulkopuolella.

Kuinka laskea kolmion alue?

Kaikenlaisen kolmion alue voidaan tietää seuraavaa kaavaa levitettäessä:

A = b x h / 2

Tässä yhtälössä viittaa alueelle; b viittaa pohjaan ja H on korkeus.

Katsotaanpa esimerkkiä. Meitä pyydetään laskemaan kolmion pinta -ala, jonka pohja on 12 senttimetriä ja jonka korkeus on 7 senttimetriä. Siten meillä on:

B = 12

H = 7

Käytämme kaavaa:

A = 12 x 7/2

A = 84/2

A = 44

Tämän kolmion siksi pinta -ala on 44 neliömetriä.