Vaaka -ammuntaominaisuudet, kaavat ja yhtälöt, harjoitukset

Hän Vaakasuuntainen ammunta Se on ammuksen lanseeraus, jolla on vaakasuuntainen nopeus tietystä korkeudesta ja jätetään painovoiman toimintaan. Kun otetaan huomioon ilman vastus, matkapuhelimen kuvaamassa etenemissuunnassa on Parabola -kaaren muoto.

Objektien heijastaminen vaakasuoraan on melko yleistä. Ammukset heitetään kaikenlaisista päistä: kivistä, joiden kanssa padot hylättiin tarinan alussa, pallourheilussa suoritetuille ja niitä seuraavat väkijoukot tiiviisti.

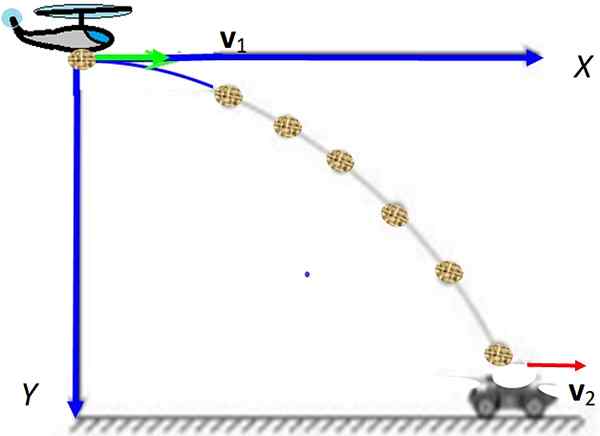
Kuvio 1. Vaakasuora ammunta punaisen nopeuden komponenteilla. Huomaa, että vaakasuora komponentti pysyy vakiona, kun taas pystysuora kasvaa. Lähde: Wikimedia Commons.

[TOC]

Ominaisuudet

Vaaka -ammunnan pääominaisuudet ovat:

-Ammukselle annettu alkuperäinen nopeus on kohtisuorassa painovoimalle.

-Liike tapahtuu koneessa, joten tarvitaan kaksi koordinaattia: x ja ja.

-Se tehdään tietystä korkeudesta h maanpinnan yläpuolella.

-Aika, jonka ammus kestää ilmassa lentoaika.

-Tekijöitä, kuten ilmankestävyyttä tai vaihtelua, ei oteta huomioon g.

-Ammuksen muoto, koko ja massa eivät vaikuta sen liikkeeseen.

-Liike hajoaa kahteen samanaikaiseen liikkeeseen: yksi pystysuora alaspäin g; Toinen vaakasuora, vakiona nopeudella.

Kaavat ja yhtälöt

Elokuvayhtälöt vaakasuuntaiseen lanseeraukseen saadaan vapaan putoamisen yhtälöistä.

Voi palvella sinua: sisäinen energia

Kuten animaatio selvästi esitetään kuvassa 1, ammus on varustettu vaakasuuntaisella alustavalla nopeudella, nimeltään v_jompikumpi = v_härkä Yllyttää (Tulostetun tekstin lihavoitu osoittaa, että se on vektori).

On huomattava, että alkuperäisellä nopeudella on suuruus v_härkä ja on suunnattu akselia pitkin x, Mikä on yksikkövektorin suunta Yllyttää. Animaatiossa varoitetaan myös, että alkuperäisellä nopeudella ei ole pystysuuntaista komponenttia, mutta kun se putoaa, tämä komponentti kasvaa tasaisesti, toiminnan ansiosta g, painovoima.

Nopeuden vaakasuoran komponentin suhteen se pysyy vakiona, kun liike kestää.

Sanotun mukaan sijainnit vahvistetaan ajan funktiona, sekä vaaka -akselilla että pystysuoralla akselilla. Oikeus otetaan +x -akseliksi, kun taas alas on osoite -ja. Painovoiman arvo on G = -9.8 m/s² jompikumpi -32 jalkaa/s²-

x (t) = x_jompikumpi + v_härkä.t (vaakasuora sijainti); v_härkä se on vakio

ja (t) = y_jompikumpi + v_Oy.T - ½ g.t² (pystysuora sijainti); v_ja = v_Oy - g.T (pystysuora nopeus)

Sijainti, nopeus, lentoaika ja maksimaalinen vaakasuuntainen alue

Yhtälöt yksinkertaistetaan, jos ne valitsevat seuraavat alkuperäiset sijainnit: x_jompikumpi = 0, ja_jompikumpi = 0 käynnistyspaikassa. sitä paitsi v_Oy = 0, Koska matkapuhelin projisoidaan vaakasuoraan. Tällä valinnalla liikkeen yhtälöt ovat tällaisia:

x (t) = v_härkä.t; v_x = v_härkä

ja (t) = - ½ g.t²; v_ja = - g.t

Kun aikaa ei ole saatavana, nopeuteen ja siirtymiin liittyvä yhtälö on hyödyllinen. Tämä pätee pystysuoraan nopeuteen, koska vaaka pysyy vakiona koko liikkeen ajan:

Voi palvella sinua: kalsiumfluori (CAF2): rakenne, ominaisuudet, käyttötarkoitukset

v_ja² = v_Oy² + 2.g .y = 2.g.ja

Lentoaika

Laskea Lentoaika t_lento, Oletetaan, että matkapuhelin projisoidaan korkeudesta H lattialla. Kun referenssijärjestelmän lähtökohta on valittu, kun se saavuttaa sen paikallaan olevaan maahan -H. Tämän korvaaminen yhtälössä 2) se saadaan:

-H = - ½ g.t²_lento

t_lento = (2h/g)^½

Enimmäisalue

Hän Vaakasuuntainen ulottuvuus Tämä aika saadaan korvaamalla x (t)-

x_Max = v_härkä. (2h/g)^½

Ratkaisut

-Liikunta ratkaistiin 1

Helikopteri lentää vaakasuoraan pitäen jatkuvan 580 metrin korkeuden, kun se vapauttaa laatikon, joka sisältää ruokaa pakolaisleirillä. Laatikko laskeutuu vaakasuoraan 150 metrin etäisyyteen sen laukaisun pisteestä. Etsi: a) laatikon lentoaika.

b) helikopterin nopeus.

c) kuinka nopeasti laatikko kosketti?

Ratkaisu

a) Korkeus H, josta ruoka vapautetaan, on H = 500 m. Näillä tiedoilla korvaamalla saat:

t_lento = (2h/g)^½= (2 x 580/9.8) ^½S = 10.9 s

b) Helikopteri kantaa vaakasuuntaista alusta v_härkä paketista ja koska yksi tiedoista on x_max-

x_Max = v_härkä. (2h/g)^½ ® v_härkä = x_Max /(2h/g)^½= x_Max / t_lento = 150 m/ 10.9 s = 13.8 m/s

c) Ammuksen nopeus milloin tahansa on:

v_ja = -g.T = -9.8 m/ s² x 10.9 s = -106.82 m/s = - 384.6 km/h

Negatiivinen merkki osoittaa, että matkapuhelin liikkuu alaspäin.

-Liikunta ratkaistiin 2

Tasosta, joka lentää vaakasuoraan korkeudella H = 500 m ja 200 km/h Paketti putoaa, jonka on pudonnut avoimeen ajoneuvoon, joka marssii 18 km/h tiellä. Missä asennossa kone antaa paketin pudota ajoneuvoon? Älä ota huomioon ilmankestävyyttä tai tuulen nopeutta.

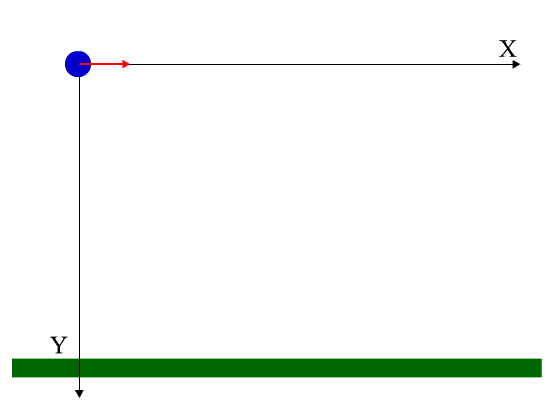
Voi palvella sinua: Dimensional AnalysisKuva 2. Harjoitusjärjestelmä ratkaistu 2. Lähde: valmistettu f. Zapata.

Ratkaisu

On kätevää siirtää kaikki yksiköt ensin kansainväliseen järjestelmään:

18 km/h = 6 m/s

200 km /h = 55 m /s

Matkapuhelimia on kaksi: taso (1) ja ajoneuvo (2), ja on tarpeen valita koordinaattijärjestelmä, jotta ne voidaan löytää molemmat. On kätevää tehdä niin lentokoneen pakkauksen lähtöpisteessä. Paketti projisoidaan vaakasuoraan tasolla, jota taso kuljettaa: v₁, kun ajoneuvo siirtyy v₂ väitetty vakio.

-Lentokone

Alkupaikka: x = 0; y = 0

Alkuperäinen nopeus = v₁ (vaakasuora)

Paikkayhtälöt: ja (t) = -½g.t²  ; x (t) = v₁.t

-Ajoneuvo

Alkupaikka: x = 0, y = -h

Alkuperäinen nopeus = v₂  (jatkuva)

x (t) = x_jompikumpi + v₂. t

Aika, jonka paketin lento kestää, on:

t_lento = (2h/g)^½ = (2 × 500/9.8)^½S = 10.1 s

Tällä hetkellä paketti on kokenut vaakasuoran siirtymisen:

x_Max = v_härkä . (2h/g)^½= 55 m/s x 10.1 s = 556 m.

Tällä hetkellä ajoneuvo on myös siirtynyt vaakasuoraan:

x (t) = v₁.T = 6 m/s x10.1 s = 60.6 m

Jos kone vapauttaa pakkauksen heti, että ajoneuvo näkee kulkevan sen alla, se ei pysty putoamaan siihen. Jotta se tapahtuu, hänen on heitettävä se takaisin:

D = 556 m - 60.6 m = 495.4 m.

Viitteet

1. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill. 74-84.
2. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Osa 1. Kinematiikka. Toimittanut Douglas Figueroa (USB).117 - 164.
3. Ammusliike. Toipunut: Phys.Librettexts.org.
4. Rex, a. 2011. Fysiikan perusteet. Pearson. 53-58.
5. Tippens, P. 2011. Fysiikka: Käsitteet ja sovellukset. 7. painos. McGraw Hill. 126-131.