Oblic Paraboliset laukausominaisuudet, kaavat, yhtälöt, esimerkit

Hän Oblic Parabolinen laukaus Se on erityinen tapaus vapaan putoamisen liikkeestä, jossa ammuksen alkuperäinen nopeus muodostaa tietyn kulman vaakasuunnassa, mikä johtaa paraboliseen polkuun.

Vapaa pudotus on liikettä jatkuvan kiihtyvyyden kanssa, jossa kiihtyvyys on painovoima, joka osoittaa aina pystysuoraan ja sen suuruus on 9,8 m/s^2. Se ei riipu ammuksen taikinasta, kuten Galileo Galilei osoitti vuonna 1604.

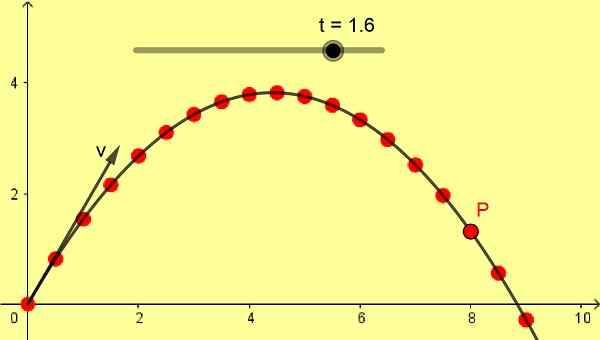Kuvio 1. Obblic Parabolinen laukaus. (Oma yksityiskohta)

Jos alkuperäinen ammuksen nopeus on pystysuora, vapaassa pudotuksessa on suora ja pystysuuntainen etenemissuunta, mutta jos alkuperäinen nopeus on vinossa, vapaan pudotuksen etenemissuunta on parabolinen käyrä, myös Galileo osoittaa.

Esimerkkejä parabolisesta liikkeestä ovat baseballia seuraava etenemissuunta, tykin ampuma luoti ja letkusta tulevan vesisuihku.

Kuvio 1 esittää vinojen parabolisen laukauksen, joka on 10 m/s kulmassa 60º. Asteikko on metreinä ja peräkkäiset P -asemat otetaan erolla 0,1 s alusta alkaen hetkestä 0 sekuntia.

[TOC]

Kaavat

Hiukkasen liikettä kuvataan kokonaan, jos sen sijainti tunnetaan, sen nopeus ja kiihtyvyys ajan funktiona.

Viblikuurasta johtuva parabolinen liike on vaakasuuntaisen liikkeen superpositio vakiona nopeudella sekä pystysuora liike, jolla on jatkuva kiihtyvyys, joka on yhtä suuri kuin painovoiman kiihtyvyys.

Kaavat, jotka koskevat vinossa parabolista laukausta a = g, Huomaa, että lihavoituna on käytetty osoittamaan, että kiihtyvyys on vektorimäärää.

Voi palvella sinua: luonnolliset satelliitit

Sijainti ja nopeus 

Jatkuvassa kiihtyvyysliikkeessä sijainti matemaattisesti riippuu ajasta neliömäisellä tavalla.

Jos tarkoitamme r -(T) Aikapäiväinen asento t, r -jompikumpi Alkuperäinen välitön sijainti, vjompikumpi Alkuperäinen nopeus, g kiihtyvyys ja t = 0 Alkuperäisenä hetkenä kaava, joka antaa sijainnin jokaiselle ajanjaksolle t On:

r -(t) = r -_jompikumpi + v_jompikumpi T + ½ g t²

Lihavoitu edellisessä lausekkeessa osoittaa, että se on vektoriyhtälö.

Nopeus ajan funktiona saadaan johdannaisen ottamisesta aseman T suhteessa ja tulos on:

v(t) = v_jompikumpi + g t

Ja kiihtyvyyden saamiseksi ajan funktiona, nopeus johdettu t Tuloksena:

-lla(t) = g

Kun aikaa ei ole saatavana, nopeuden ja sijainnin välillä on suhde, jonka antaa:

v² = vjompikumpi² - 2 g (ja - minä)

Yhtälöt

Seuraavaksi löydämme yhtälöt, joita sovelletaan vinoon paraboliseen laukaukseen Cartesian muodossa.

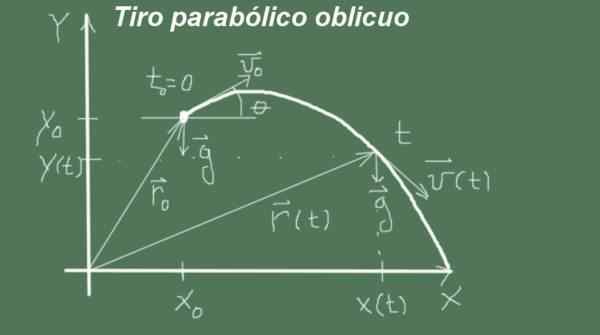
Kuva 2. Vinossa parabolisen laukauksen muuttujat ja parametrit. (Oma yksityiskohta)

Liike alkaa tällä hetkellä t = 0 Alkuperäisellä sijainnilla (Xo, minä) ja suuruusnopeus vjompikumpi ja kulma θ, toisin sanoen alkuperäinen nopeusvektori on (Vjompikumpi cosθ, vjompikumpi Senθ). Liike kulkee kiihtyvyydellä 

g = (0, -g).

Parametriset yhtälöt

Jos vektorikaava, joka antaa sijainnin ajan funktiona ja komponentit ryhmitetään ja tasoitetaan, aseman koordinaattien antamat yhtälöt saadaan aikaan t saadaan aikaan t.

x (t) = x_jompikumpi + v_härkä t 

ja (t) = y_jompikumpi + v_Oy t -½ g t²

Samoin yhtälöillä on nopeuskomponentit aikafunktiona.

Se voi palvella sinua: Normaali työ: mistä se koostuu, miten se lasketaan, esimerkkejä

v_x(t) = v_härkä

v_ja(t) = v_Oy - G T 

Missä: v_härkä = vjompikumpi cosθ; v_Oy = vjompikumpi Sentr

Suuntaviivayhtälö

y = a x^2 + b x + c

A = -g/(2 Vhärkä^2)

B = (vOy/vhärkä + G Xjompikumpi/vhärkä^2)

C = (jajompikumpi - vOy xjompikumpi / vhärkä-A

Esimerkit 

Esimerkki 1

Vastaa seuraaviin kysymyksiin:

a) Miksi parabolisissa ammuntaongelmissa yleensä halveksii kitkan vaikutusta ilmalla?

b) Onko esineen muoto parabolisessa laukauksessa?

Vastaukset

a) Jotta ammuksen liikkuminen on parabolinen, on tärkeää, että ilman kitkavoima on paljon alhaisempi kuin käynnistetyn esineen paino. 

Jos korkkipallo tai jokin kevyt materiaali heitetään, kitkavoima on verrattavissa painoon ja sen etenemissuunta ei voi lähestyä parabolia.

Päinvastoin, jos se on raskas esine kuin kivi, kitkavoima on vähäinen verrattuna kiven painoon ja sen etenemiseen on lähellä parabolia.

b) Käytetyn esineen muoto on myös merkityksellinen. Jos käynnistetään lentokoneen plataso Avionnciton muodossa, sen liike ei ole vapaa tai parabolinen, koska muoto suosii ilmankestävyyttä.

Toisaalta, jos sama paperiarkki on kompakti pallon muodossa, tuloksena oleva liike on hyvin samanlainen kuin parabola.

Esimerkki 2

Ammus käynnistetään vaakasuorasta lattiasta nopeasti 10 m/s ja 60º kulma. Nämä ovat samoja tietoja, joiden kanssa kuva 1 kehitettiin. Näiden tietojen kanssa löydän:

a) hetki, jolloin se saavuttaa enimmäiskorkeuden.

Voi palvella sinua: mitkä ovat lämpöominaisuudet ja mitkä ovat? (Esimerkkejä)

b) enimmäiskorkeus.

c) nopeus enimmäiskorkeudella.

d) sijainti ja nopeus 1,6 s.

e) hetki, jolloin hän pelaa uudelleen maaperää.

f) Vaaka -alue.

Ratkaisu)

Pystysuuntainen nopeus ajasta riippuen on

v_ja(t) = v_Oy - G t = v_jompikumpi Senθ - g t = 10 sen60º - 9.8 T = 8.66 - 9.8 t 

Kun enimmäiskorkeus saavutetaan, pystysuuntainen nopeus on nolla välittömästi.   

8.66 - 9.8 t = 0 ⇒ t = 0.88 s.

Ratkaisu b)

Suurin korkeus annetaan koordinaatilla ja Tällä hetkellä, jolloin tämä korkeus saavutetaan:

ja (0.88S) = Yo minä t -½ g t^2 = 0 + 8.66*0.88-½ 9.8 0.88^2 = 

3.83 m

Siksi enimmäiskorkeus on 3.83 m.

Liuos c)

Nopeus enimmäiskorkeudella on vaakasuora:

v_x(t) = v_härkä = v_jompikumpi cosθ = 10 cos60º = 5 m/s 

D) liuos

Sijainti 1.6 s on:

X (1.6) = 5*1,6 = 8,0 m

ja (1.6) = 8.66*1.6-½ 9.8 1.62 = 1.31 m

Ratkaisu e)

Kun koordinaatti koskettaa ja se peruutetaan, sitten:

ja (t) = 8.66*t -½ 9.8 t2 = 0 ⇒ T = 1,77 s

Ratkaisu f)

Vaaka -alue on X -koordinaatti heti, joka pelaa maaperää:

X (1.77) = 5*1,77 = 8,85 m

Esimerkki 3

Löydä suuntayhtälö esimerkki 2 -tiedoista.

Ratkaisu 

Etenemissuunnan parametrinen yhtälö on:

x (t) = 5*t

ja (t) = 8.66*t -½ 9.8 T^2

Ja Cartesian yhtälö saadaan puhdistamalla ensimmäisen T ja korvaamalla toisessa

y = 8.66*(x/5) -½ 9.8 (x/5)^2

Yksinkertaistaminen:

y = 1,73 x - 0,20 x^2 

Viitteet

1. P. P. Teodorescu (2007). "Kinematiikka". Mekaaniset järjestelmät, klassiset mallit: hiukkasmekaniikka. Jousto.
2. Resnick, Halliday & Krane (2002). Fysiikan osa 1. Cecsa, Meksiko.
3. Thomas Wallace Wright (1896). Mekaniikan elementit, mukaan lukien kinematiikka, kinetiikka ja statiikka. E ja FN SPON.
4. Wikipedia. Parabolinen liike. ES: stä palautettu.Wikipedia.org.
5. Wikipedia. Ammusliike.Haettu jstk.Wikipedia.org.