Pystysuora ammuntakaavat, yhtälöt, esimerkit

Hän pystysuora ammunta Se on liike, joka tapahtuu voimien kentän, yleisesti painovoiman, kyvyn nousevan tai laskevan alaisuudessa. Se tunnetaan myös nimellä Pystysuora käynnistys.

Välitön esimerkki heitetään ylös (tai alas, jos se on suositeltava) pallo kädelläsi, kyllä, varmista, että teet sen pystysuunnassa. Ilmankestävyyden halveksittava liike, joka seuraa palloa, sopii täydellisesti tasaisesti monipuoliseen suorakulmaiseen liikkumismalliin (MRUV).

Kuvio 1. Pallonpilän puhuminen on hyvä esimerkki pystysuorasta laukauksesta. Lähde: Pexels.

Pystysuora ammunta on laajalti tutkittu liike fysiikan johdantokursseilla, koska se on näyte liikkuminen ulottuvuudessa, Hyvin yksinkertainen ja hyödyllinen malli.

Tätä mallia ei voida käyttää vain esineiden kinematiikan tutkimiseen painovoiman vaikutuksen alla, vaan myös, kuten myöhemmin nähdään, kuvaa hiukkasten liikkumista tasaisen sähkökentän keskellä.

[TOC]

Kaavat ja yhtälöt

Ensimmäinen tarvittava asia on koordinaattijärjestelmä, joka osoittaa alkuperän ja merkitä se kirjaimella, joka pystysuorien liikkeiden tapauksessa on kirjain "ja".

Sitten positiivinen merkitys valitaan +ja, joka on yleensä ylös ja merkitys -ja Se yleensä otetaan alas (katso kuva 2). Kaikki tämä, ellei se ratkaise ongelmaa, päättää toisin, koska toinen vaihtoehto on ottaa yhtä positiivinen liikkeen suunta, riippumatta siitä, mikä tämä on.

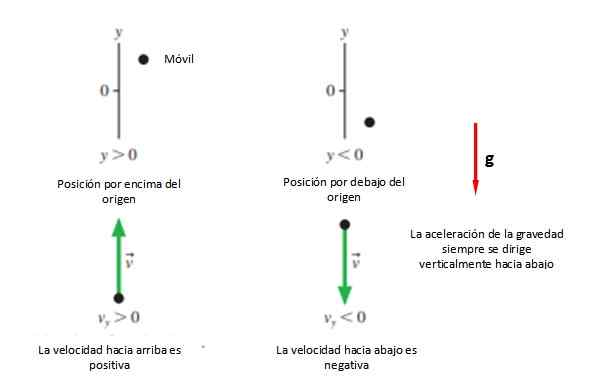Kuva 2. Tavalliset merkinnän yleissopimus pystysuorassa laukauksessa. Lähde: f. Zapata.

Joka tapauksessa suositellaan, että alkuperä on samaan aikaan käynnistyksen kohdan kanssa ja_jompikumpi, Koska yhtälöt yksinkertaistetaan, vaikka mitä tahansa halutun aseman voidaan aloittaa liikkeen tutkimisen aloittamiseksi.

Se voi palvella sinua: Toinen tasapainotila: Selitys, esimerkit, harjoitukset

Pystysuora ammuntayhtälö

Kun koordinaattijärjestelmä ja alkuperä on perustettu, siirrymme yhtälöihin. Liikettä kuvaavat suuruudet ovat:

-Alkunopeus v_jompikumpi

-Kiihtyvyys -lla

-Nopeus v

-Alkupaikka x_jompikumpi

-Sijainti x

-Siirtymä D -dx

-Aika t

Kaikki paitsi aika ovat vektoreita, mutta koska se on yhden ulottuvuuden liike, jolla on tiety. Pystysuoran ammunnan tapauksessa painovoima menee aina alas ja ellei toisin mainita, merkki myönnetään -.

Sitten on yhtälöitä, jotka on mukautettu pystysuuntaiseen ammuntaan, korvaamalla "x"Kirjoittaja"ja"Ja"-lla"Kirjoittaja"g". Lisäksi merkki (-) vastaa ohjeita:

1) sijainti- y = y_jompikumpi + v_jompikumpi.T - ½ g.t²

2) Nopeus- V = V_jompikumpi - g.t

3) nopeus siirtymästä δ riippuenja- v² = v_jompikumpi² - 2.g. Δja

Esimerkit

Sitten on sovellusesimerkkejä pystysuunnasta. Seuraavat päätöslauselmassa on otettava huomioon:

-"g”Sillä on vakioarvo, joka on keskimäärin 9,8 m/s² tai noin 10 m/s² Jos halutaan helpottaa laskelmia, kun ei vaadita liian tarkkuutta.

-Kun v_jompikumpi Hyvä 0 -, Nämä yhtälöt vähenevät vapaa pudotus.

-Jos käynnistys on ylöspäin, objektilla on oltava alkuperäinen nopeus, jonka avulla voit liikkua. Liikettäessä objekti saavuttaa enimmäiskorkeuden, joka riippuu siitä, kuinka suuri alkuperäinen nopeus on. Tietysti korkeampaan korkeuteen matkapuhelin viettää enemmän aikaa ilmassa.

-Kohde palaa lähtöpisteeseen samalla nopeudella, jolla se käynnistettiin, mutta nopeus on suunnattu alas.

-Pystysuoraan laukaisuun, mitä suurempi alkuperäinen nopeus, sitä nopeammin esine saapuu maahan. Täällä kulkenut etäisyys on kiinnitetty valitun korkeuden mukaan.

Voi palvella sinua: mikä on suhteellinen ja ehdoton karheus?

-Pystysuorassa laukauksessa aika, joka vie matkapuhelimen saavuttamaan enimmäiskorkeuden, lasketaan tekemällä V = 0 Edellisen osan yhtälössä 2). Tämä on enimmäisaika t_Max-

0 = V_jompikumpi - g . t_Max ⇒ t_Max = v_jompikumpi /g

-Se enimmäiskorkeus ja_Max Se tyhjentää myös edellisen osan yhtälöstä 3) V = 0-

0 = V_jompikumpi² - 2.g. ΔY ⇒ 0 = V_jompikumpi² - 2.g. (ja_Max - ja_jompikumpi) ⇒ ja_Max = y_jompikumpi  + v_jompikumpi² / 2 g

Joo ja_jompikumpi = 0, Se on pelkistetty:

ja_Max = v_jompikumpi² / 2 g

Ratkaistu esimerkki 1

V -pallo heitetään pystysuoraan ylöspäin_jompikumpi = 14 m/s, 18 m korkean rakennuksen yläosasta. Pallo saa seurata alavirtaan jalkakäytävälle. Laskea:

a) Pallo saavutti suurin korkeus maahan nähden.

b) Aika ilmassa (lentoaika-A.

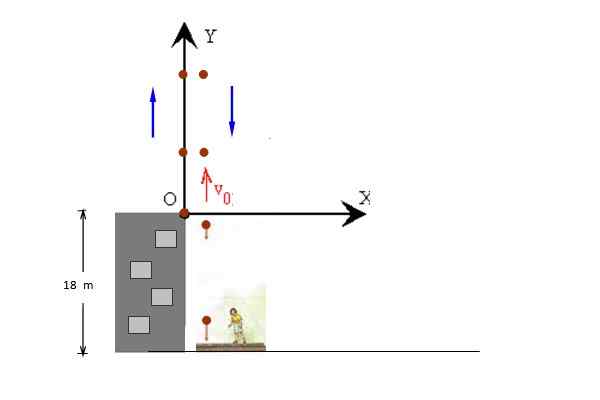Kuva 3. Pallo heitetään pystysuoraan rakennuksen katolta. Lähde: f. Zapata.

Ratkaisu

Kuvassa pallon nousun ja laskun liikkeet ilmestyvät erikseen selvyyden vuoksi, mutta molemmat tapahtuvat samalla linjalla. Alkupaikka otetaan y = 0, niin että lopullinen sijainti on y = - 18 m.

a) Rakennuksen katosta mitattu enimmäismitta on ja_Max = v_jompikumpi² / 2 g Ja lausunnosta luetaan, että alkuperäinen nopeus on +14 m/s, sitten: sitten:

ja_Max = (14 m/s)² / 2 x 9.8 m/s² = 10 m (Katon suhteen)

H_Max = 10 m + 18 m = 28 m (Jalkakäytävän suhteen).

b) löytää Kokonaisaika jompikumpi lentoaika Ilmassa kestävää palloa käytetään yhtälöön y = y_jompikumpi + v_jompikumpi.T - ½ g.t², Seuraavilla arvoilla ja merkkeillä:

y = - 18 m

ja_jompikumpi = 0 m

v_jompikumpi = +14 m/s

Korvaus:

- 18 = 14.T - ½ 9.8 .t²

- 4.9 t²+14.T + 18 = 0 

4.9 t²-14.T - 18 = 0

Se on toisen asteen yhtälö, joka on helposti ratkaistu tieteellisen laskimen avulla tai tarkkuuden avulla. Ratkaisut ovat: 3.82 ja -0.96. Negatiivinen ratkaisu hylätään, koska on aika, jolla ei ole fyysistä merkitystä.

Se voi palvella sinua: Lämpö: Kaavat ja yksiköt, ominaisuudet, miten se mitataan, esimerkkejä

Pallon lentoaika on 3.82 sekuntia.

Ratkaistu esimerkki 2

Positiivisesti ladattu hiukkas Q = +1.2 milicoulombs (MC) ja massa M = 2.3 x 10 ^-10 Kg Se projisoidaan pystysuunnassa, alkaen kuvassa esitetystä sijainnista ja alkuperäisellä nopeudella v_jompikumpi = 30 km/s.

Ladattujen levyjen joukossa on sähkökenttä JA tasainen, suunnattu pystysuunnassa alas ja suuruus 780 N/C. Jos levyjen välinen etäisyys on 18 cm, törmäätkö hiukkasen ylemmän levyn kanssa? Halveksia hiukkasten painovoimaa, koska se on erittäin kevyt.

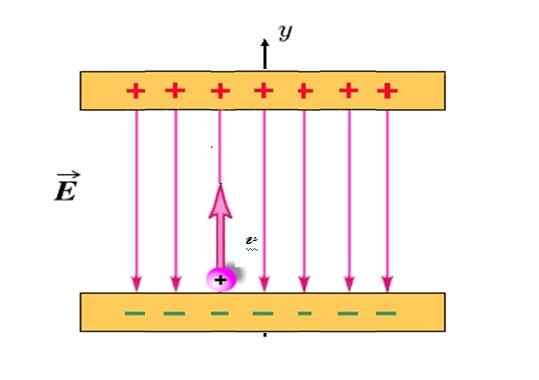Kuva 4. Positiivinen kuormituspartikkeli liikkuu samanlaisena kuin pystysuoraan heitetty pallo, kun se upotetaan kuvan sähkökenttään. Lähde: Muokattu f. Wikimedia Commons Shoe.

Ratkaisu

Tässä ongelmassa sähkökenttä JA on se, joka tuottaa voiman F ja siitä johtuva kiihtyvyys. Positiivisesti ladattuna hiukkanen houkutellaan aina alempaan levyyn, mutta kun se projisoidaan pystysuoraan ylöspäin, se saavuttaa maksimikorkeuden ja palaa sitten alempaan levyyn, kuten edellisten esimerkkien palloon.

Sähkökentän määritelmän mukaan:

E = f/q = m.A /q ⇒ a = q.E / M

Tätä vastaavuutta on tarpeen käyttää ennen arvojen korvaamista:

1 mc = 1 x 10^-3 C

Tämän kanssa kiihtyvyys on:

A = 1.2 x 10^-3 X 780/2.3 x 10 ^-10neiti² = 4.07 x 10⁹ neiti²

Suurimpaan korkeuteen käytetään edellisen osan kaavaa, mutta sen sijaan, että käyttäisivät ”g"Tätä kiihtyvyysarvoa käytetään:

ja_Max = v_jompikumpi² / 2a = (30.000 m/s)²/2 x 4.07 x 10⁹ neiti² = 0.11 m = 11 cm

Älä törmää ylemmän levyn kanssa, koska se on 18 cm lähtökohdasta, ja hiukkanen heti, kun se nostaa 11 cm.

https: // youtu.Be/kt08ntudzwq

Viitteet

1. Kirkpatrick, L. 2007. Fysiikka: Katsaus maailmaan. 6^ta Lyhennetty painos. Cengage -oppiminen. 23 - 27.
2. Rex, a. 2011. Fysiikan perusteet. Pearson. 33 - 36
3. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14^th. Ed. Osa 1. 50 - 53.
4. Serway, R., ULOLE, c. 2011. Fysiikan perusteet. 9^naa Ed. Cengage -oppiminen. 43 - 55.
5. Wilson, J. 2011. Fysiikka 10. Pearson -koulutus. 133 - 149.